【OpenCV】OpenCV基础教程（5）—— 阈值分割

5. 阈值分隔

5.1 全局阈值分隔

全局阈值分割指的是将灰度值大于 thresh（阈值）的像素设为白色，小于或者等于 thresh 的像素设为黑色；或者反过来，将大于 thresh 的像素设为黑色，小于或者等于 thresh 的像素设为白色，两者的区别只是呈现形式不同。

OpenCV提供的函数如下：

double cv::threshold(cv::InputArray src, cv::OutputArray dst, double thresh, double maxval, int type)

src：单通道矩阵，数据类型为 CV_8U 或者 CV_32F。type = THRESH_OTSU 或 THRESH_TRIANGLE 时，src 只支持 uchar 类型。

dst：输出矩阵，即阈值分割后的矩阵

thresh：阈值

maxVal：在图像二值化显示时，一般设置为 255

type：阈值分隔类型

使用方法如下：

//输入矩阵为 5 行 3列
Mat src = (Mat_<uchar>(5, 3) << 123, 234, 68, 33, 51, 17,
48, 98, 234, 129, 89, 27, 45, 167, 134);
//第一种情况：手动设置阈值
double the = 150;
Mat dst;
threshold(src, dst, the, 255, THRESH_BINARY);
//第二种情况：Otsu 算法
double otsuThe=0;
Mat dst_Otsu;
otsuThe = threshold(src, dst_Otsu, otsuThe, 255, THRESH_OTSU + THRESH_BINARY);
//第三种情况：TRIANGLE 算法
double triThe=0;
Mat dst_tri;
triThe = threshold(src, dst_tri, 0, 255, THRESH_TRIANGLE + THRESH_BINARY);
return 0;

---

5.1.1 利用熵算法计算阈值

信息熵（entropy）的概念来源于信息论，假设信源符号 有 种取值，记为
$$u_1,u_2,\cdots ,u_N$$
且每一种信源符号出现的概率，记为
$$p_1,p_2,\cdots ,p_N$$
那么该信源符号的信息熵，记为
$$\text{entropy}(u)=-\sum _{i=1}^N{p}_i\log p_i$$
图像也可以看作一种信源，假设输入图像为$\mathbf{I}$，$\text{normHis}{\text{t}}_{\mathbf{I}}$代表**归一化**的图像灰度直方图，那么对于 8 位图可以看成由 256 个灰度符号，且每一个符号出现的概率为$\text{normHis}{\text{t}}_{\mathbf{I}}(k)$组成的信源，其中 0 ⩽ ⩽ 255。

利用熵计算阈值的步骤如下：

第一步：计算$\mathbf{I}$的累加概率直方图，又称零阶累积矩，记为
$$\text{cumuHist}(k)=\sum _{i=0}^k\text{normHis}{\text{t}}_{\mathbf{I}}(k),k\in [0,255]$$
第二步：计算各个灰度级的熵，记为
$$\text{entropy}(t)\text{=}-\sum _{k=0}^t\text{normHis}{\text{t}}_{\mathbf{I}}(k)\log (\text{normHis}{\text{t}}_{\mathbf{I}}(k)),t\in [0,255]$$
第三步：计算使$f(t)=f_1(t)+f_2(t)$最大化的$t$值，该值即为得到的阈值，其中
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ & {{f}_{1}}(…

5.2 局部阈值分隔（自适应阈值分隔）

背景：光照不均的情况下，全局阈值分隔的效果不是很理想。在这种情况下，使用局部阈值（自适应阈值）进行分隔可以产生好的效果。

局部阈值分隔不再像全局阈值一样，对整个矩阵只有一个阈值，而是针对输入矩阵的每一个位置的值都有相对应的阈值，这些阈值构成了和输入矩阵同等尺寸的矩阵$\mathbf{t}\mathbf{h}\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{h}$。

---

局部阈值分隔的核心是计算阈值矩阵，方法如下：

第一步：对图像进行平滑处理，平滑结果记为$f_{\text{smooth}}(\mathbf{I})$，其中平滑可以是均值平滑、高斯平滑、中值平滑，但是平滑算子的宽和高必须都是奇数。

第二步：自适应阈值矩阵$\mathbf{T}\mathbf{h}\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{h}=(1-\text{ratio})\cdot f_{\text{smooth}}(\mathbf{I})$，一般令$\text{ratio}=0.15$。

第三步：利用局部阈值分隔的规则进行阈值分隔。

---

在自适应阈值处理中，平滑算子的尺寸决定了分割出来的物体的尺寸，如果滤波器尺寸太小，那么估计出的局部阈值将不理想。凭经验，平滑算子的宽度必须大于被识别物体的宽度，平滑算子的尺寸越大，平滑后的结果越能更好地作为每个像素的阈值的参考，当然也不能无限大。

OpenCV提供的自适应阈值函数如下：

void cv::adaptiveThreshold(cv::InputArray src, cv::OutputArray dst, double maxValue, int adaptiveMethod, int thresholdType, int blockSize, double C)

src：单通道矩阵，数据类型为 CV_8U

dst：输出矩阵，即阈值分割后的矩阵

maxValue：与函数 Threshold 类似，一般取 255

adaptiveMethod：

​ ADAPTIVE_THRESH_MEAN_C：采用均值平滑

​ ADAPTIVE_THRESH_GAUSSIAN_C：采用高斯平滑

thresholdType：THRESH_BINARY、THRESH_BINARY_INV

blockSize：平滑算子的尺寸，且为奇数

C：比例系数。这个参数实际上是一个偏移值调整量，用均值和高斯计算阈值后，再减或加这个值就是最终阈值。

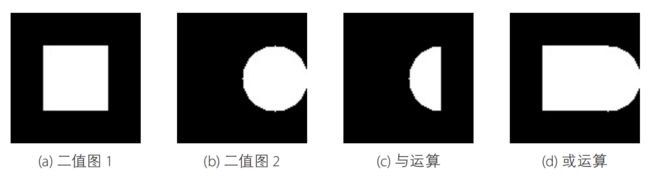
5.3 二值图的逻辑运算

“与”运算

void cv::bitwise_and(cv::InputArray src1, cv::InputArray src2, cv::OutputArray dst, cv::InputArray mask = noArray())

“或”运算

void cv::bitwise_or(cv::InputArray src1, cv::InputArray src2, cv::OutputArray dst, cv::InputArray mask = noArray())

效果如下：