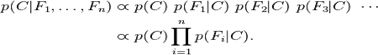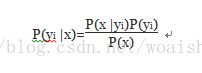数据挖掘分类方法探究----朴素贝叶斯方法

1.      数据挖掘概念

数据挖掘是从大量的、不完全的、有噪声的、模糊的、随机的数据集中识别有效的、新颖的、潜在有用的，以及最终可理解的模式的非平凡过程。它是一门涉及面很广的交叉学科，包括机器学习、数理统计、神经网络、数据库、模式识别、粗糙集、模糊数学等相关技术。

它是一门受到来自各种不同领域的研究者关注的交叉性学科，又有人称之为“知识发现”，相对来讲，数据挖掘主要流行于统计界（最早出现于统计文献中）、数据分析、数据库和管理信息系统界；而知识发现则主要流行于人工智能和机器学习界。

数据挖掘可粗略地理解为三部曲：数据准备（data preparation）、数据挖掘，以及结果的解释评估。数据准备是从相关的数据源中选取所需的数据并整合成用于数据挖掘的数据集；规律寻找是用某种方法将数据集所含的规律找出来；规律表示是尽可能以用户可理解的方式（如可视化）将找出的规律表示出来。

数据挖掘的任务有关联分析、聚类分析、分类分析、异常分析、特异群组分析和演变分析，等等。本文中主要讨论分类分析中的朴素贝叶斯方法，在讨论朴素贝叶斯方法之前，来区分一下分类与聚类的概念。

2.      分类与聚类

分类（Classification）是一种监督学习，它找出描述并区分数据类或概念的模型(或函数)，以便能够使用模型预测类标记未知的对象类。分类的目的是学会一个分类函数或分类模型(也常常称作分类器),该模型能把数据库中的数据项映射到给定类别中的某一个类中。分类和回归都可用于预测，两者的目的都是从历史数据纪录中自动推导出对给定数据的推广描述，从而能对未来数据进行预测。与回归不同的是，分类的输出是离散的类别值，而回归的输出是连续数值。二者常表现为决策树的形式，根据数据值从树根开始搜索，沿着数据满足的分支往上走，走到树叶就能确定类别。要构造分类器，需要有一个训练样本数据集作为输入。训练集由一组数据库记录或元组构成，每个元组是一个由有关字段(又称属性或特征)值组成的特征向量，此外，训练样本还有一个类别标记。一个具体样本的形式可表示为：（v1,v2,...,vn; c)；其中vi表示字段值，c表示类别。常用的分类算法包括：决策树分类法，朴素的贝叶斯分类算法(native Bayesian classifier)、基于支持向量机(SVM)的分类器，神经网络法，k-最近邻法(k-nearest neighbor，kNN)，模糊分类法等等。

对于分类，有三种分类器评价或比较尺度：

1) 预测准确度；2)计算复杂度；3)模型描述的简洁度。

预测准确度是用得最多的一种比较尺度，特别是对于预测型分类任务。计算复杂度依赖于具体的实现细节和硬件环境，在数据挖掘中，由于操作对象是巨量的数据，因此空间和时间的复杂度问题将是非常重要的一个环节。对于描述型的分类任务，模型描述越简洁越受欢迎。

另外要注意的是，分类的效果一般和数据的特点有关，有的数据噪声大，有的有空缺值，有的分布稀疏，有的字段或属性间相关性强，有的属性是离散的而有的是连续值或混合式的。目前普遍认为不存在某种方法能适合于各种特点的数据。

聚类(clustering)是一种无监督学习，是指根据“物以类聚”的原理，将本身没有类别的样本聚集成不同的组，这样的一组数据对象的集合叫做簇，并且对每一个这样的簇进行描述的过程。它的目的是使得属于同一个簇的样本之间应该彼此相似，而不同簇的样本应该足够不相似。与分类规则不同，进行聚类前并不知道将要划分成几个组和什么样的组，也不知道根据哪些空间区分规则来定义组。其目的旨在发现空间实体的属性间的函数关系，挖掘的知识用以属性名为变量的数学方程来表示。与分类不同，无监督学习不依赖预先定义的类或带类标记的训练实例，需要由聚类学习算法自动确定标记，而分类学习的实例或数据样本有类别标记。聚类学习是观察式学习，而不是示例式学习，常见的聚类算法包括：K-均值聚类算法、K-中心点聚类算法、CLARANS、BIRCH、CLIQUE、DBSCAN

3. 朴素贝叶斯分类方法

（1）贝叶斯定理

已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。

（2）贝叶斯模型

理论上，概率模型分类器是一个条件概率模型。

P(C  | F_1, F_2………..F_n )

独立的类别变量有若干类别，条件依赖于若干特征变量 F1，F2，.......FN。但问题在于如果特征数量较大或者每个特征能取大量值时，基于概率模型列出概率表变得不现实。所以我们修改这个模型使之变得可行。 贝叶斯定理有以下式子：

实际中，我们只关心分式中的分子部分，因为分母不依赖于C而且特征F的值是给定的，于是分母可以认为是一个常数。这样分子就等价于联合分布模型。

对于我们来说，先验概率P(C) 我们可以凭借领域专家经验来得到，而P(F1，…….FN |C)计算在有大量特征属性或者特征属性有大量值时不易求出。由重复使用链式法则，可将该式写成条件概率的形式，如下所示：

由此可知这个工作量是很大的。而朴素贝叶斯分类方法使用了大胆而激进的方式，假设所有特征变量是相互独立的。这就意味着对于i≠j，P(F_i|C, F_j)= P(F_i|C)

所以联合分布模型可以表达为

由此可以得到朴素贝叶斯分类方法的定义。

（3）朴素贝叶斯分类的正式定义

 <1>设x={a_1, a_{2, ……}a_m}为一个待分类项，而每个a为x的一个特征变量。

<2>有类别集合C={y_1, y_{2 ……}y_n}其中y是不同的类别。

<3>分别计算 P(y₁|x), P(y₂|x),…… P(y_n|x)

<4>求出其中最大值，如果  P(y_k|x)=max{ P(y₁|x),P(y₂|x), …… P(y_n|x)} 则 x∈y_k

那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

1）找到一个已知分类的待分类项集合，这个集合叫做训练样本集。获得先验概率以及得到已知训练样本的分布情况或者计算条件概率所需的参数

2）统计得到在各类别下各个特征变量的条件概率估计。即

P(a₁|y₁)P(a₂|y₁) …P(a_m|y₁), P(a₁|y₂)P(a₂|y₂) …P(a_m|y₂) ,P(a₁|y_n)P(a₂|y_n)…P(a_m|y_n)

3）则根据贝叶斯定理有如下推导：           

 

因为分母对于所有类别为常数，因此我们只要将分子最大化即可。又因为朴素贝叶斯假设各特征变量是条件独立的，所以有：    

  

4）这样便可以得到所要分类项x属于每一个类别y_i的概率，从中选取最大的，则便得到分类项所属的类别。

可以看到，整个朴素贝叶斯分类分为三个阶段：

第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

由上文得知，求条件概率是朴素贝叶斯分类的关键步骤，对于特征变量是离散值来说求其概率可以用频率求出概率，对于值是连续数据时我们一般会使用其概率密度（确定其分布情况）。下面介绍一个实例帮助我们理解。

4.朴素贝叶斯分类实例

性别分类

（1）问题描述

通过一些测量的特征，包括身高、体重、脚的尺寸，判定一个人是男性还是女性。

首先，这里所要分类项的特征向量集合为X(height，weight，footsize)，类别集合为C（male，female）

（2）训练数据

性别	身高(英尺)	体重(磅)	脚的尺寸(英寸)
男	6	180	12
男	5.92 (5'11")	190	11
男	5.58 (5'7")	170	12
男	5.92 (5'11")	165	10
女	5	100	6
女	5.5 (5'6")	150	8
女	5.42 (5'5")	130	7
女	5.75 (5'9")	150	9

假设训练集样本的特征满足高斯分布，得到下表：

性别	均值(身高)	方差(身高)	均值(体重)	方差(体重)	均值(脚的尺寸)	方差（脚的尺寸）
男性	5.855	3.5033e-02	176.25	1.2292e+02	11.25	9.1667e-01
女性	5.4175	9.7225e-02	132.5	5.5833e+02	7.5	1.6667e+00

先说明一下高斯分布（即正态分布），若随机变量x服从一个位置参数为μ（均值）、尺度参数为σ（标准差）的概率分布，且其概率密度函数为：

                        

我们认为两种类别是等概率的，也就是P(male)= P(female) = 0.5。在没有做辨识的情况下就做这样的假设并不是一个好的点子。但我们通过数据集中两类样本出现的频率来确定P(C)，我们得到的结果也是一样的。

（3）测试

以下给出一个待分类是男性还是女性的样本

性别	身高(英尺)	体重(磅)	脚的尺寸(英尺)
sample	6	130	8

我们希望得到的是男性还是女性哪类的后验概率大。由贝叶斯公式得知，我们只考虑分子就可以了，那么我们可以用下面的式子来比较两种类别的后验概率：

该分类是男性的概率：

P(male)P(height | male) P(weight | male) P(footsize | male)

该分类是女性的概率：

P(female)P(height | male) P(weight | male) P(footsize | male)

我们可以求得x中的每个特征变量对应各个分类的条件概率（密度），例如，我们在这里求得height对应male类别的条件概率。

, 其中μ=5.855，σ²=3.5033e^-2，是训练集样本的正态分布参数.注意，这里的值大于1也是允许的 –这里是概率密度而不是概率，因为身高是一个连续的变量.类似的，我们可以求出其他特征变量对应各个类别的条件概率：

P(weight | male)=5.9881e^-6‑

P(footsize |male)=1.3112e^-3

P(height | female)=2.2346e^-1

P(weight | female)=1.6789e^-2

P(footsize | female)=2.8669e^-1

上面提到P(male)=P(female)=0.5，所以所需的值都已经求出，代入上面的公式算出结果：

Posteriornumerator(male)= 6.1984e^-9

Posteriornumerator(female)= 5.3778e^-4

由于女性后验概率的分子比较大，所以我们预计这个样本是女性。

（4）评估

   通常使用回归测试来评估分类器的准确率，最简单的方法是用构造完成的分类器对训练数据进行分类，然后根据结果给出正确率评估。但这不是一个好方法，因为使用训练数据作为检测数据有可能因为过分拟合而导致结果过于乐观，所以一种更好的方法是在构造初期将训练数据一分为二，用一部分构造分类器，然后用另一部分检测分类器的准确率

5.样本修正

 如果一个给定的类和特征值在训练集中没有一起出现过，那么基于频率的估计下该概率将为0。这将是一个问题。因为与其他概率相乘时将会把其他概率的信息统统去除。所以常常要求要对每个小类样本的概率估计进行修正，以保证不会出现有为0的概率出现。为了解决这个问题，我们可以引入Laplace校准，它的思想非常简单，就是对没类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面。

6.朴素贝叶斯分类的优缺点

尽管实际上独立假设常常是不准确的，但朴素贝叶斯分类器的若干特性让其在实践中能够取得令人惊奇的效果。特别地，各类条件特征之间的解耦意味着每个特征的分布都可以独立地被当做一维分布来估计。这样减轻了由于维数灾带来的阻碍,当样本的特征个数增加时就不需要使样本规模呈指数增长。然而朴素贝叶斯在大多数情况下不能对类概率做出非常准确的估计，但在许多应用中这一点并不要求。例如，朴素贝叶斯分类器中，依据最大后验概率决策规则只要正确类的后验概率比其他类要高就可以得到正确的分类。所以不管概率估计轻度的甚至是严重的不精确都不影响正确的分类结果。在这种方式下，分类器可以有足够的鲁棒性去忽略朴素贝叶斯概率模型上存在的缺陷。

参考文献

1. 数据挖掘领域十大经典算法初探；

2.  维基百科http://zh.wikipedia.org/wiki/朴素贝叶斯分类器；

3．CodingLabs博客，http://www.cnblogs.com/；

4．数据挖掘导论，[美] Pang-Ning Tan / Michael Steinbach / Vipin Kumar 著；