Improving unsupervised defect segmentation by applying structural similarity to autoencoders
Improving unsupervised defect segmentation by applying structural similarity to autoencoders
- Abstract
- 1. Introduction
- 2. Related Work
- 3. Methodology
-
- 3.1. Autoencoders for Unsupervised Defect Segmentation
-
- 3.1.1. l 2 l^2 l2-Autoencoder
- 3.1.2. Variational Autoencoder
- 3.1.3. Feature Matching Autoencoder
- 3.1.4. SSIM Autoencoder
- 3.2. Structural Similarity
- 4. Experiments
-
- 4.1. Datasets
- 4.2. Training and Evaluation Procedure
文章链接:https://arxiv.org/pdf/1807.02011.pdf
Abstract
卷积自动编码器已经成为图像数据上无监督缺陷分割的流行方法。通常,此任务是通过设置基于 l p − l^p- lp−距离的逐像素的重建误差的阈值执行的。然而,当边缘存在轻微的定位不准时, l p − l^p- lp−距离会导致大的残差,并且当强度值保持大致一致时,它也不能揭示视觉上被改变的缺陷区域。我们的研究表明,这些问题使这些方法无法应用于复杂的现实场景,而且使用更复杂的架构(如变分或特征匹配自动编码器)也无法轻易避免这些问题。我们建议使用基于结构相似性的感知损失函数来检查局部图像区域之间的相互依赖关系,结构相似性考虑亮度、对比度和结构信息,而不是简单地比较单个像素值。它在具有挑战性的真实世界的纳米纤维材料数据集和两个机织织物的新数据集上,对比通过使用逐像素重构误差度量的最先进的无监督缺陷分割方法取得了显著的性能增益。
1. Introduction
觉检测在工业制造中是必不可少的,它可以通过快速丢弃有缺陷的部件来保证高质量和高成本效率。由于人工检查速度慢、成本高且容易出错,使用全自动计算机视觉系统变得越来越流行。通常使用的是监督方法,系统通过对缺陷样本和非缺陷样本的训练来学习如何分割缺陷区域。然而,它们涉及到注释数据的大量工作,并且需要事先知道所有可能的缺陷类型。此外,在一些生产过程中,报废率可能太小,无法产生足够数量的缺陷样本用于训练,特别是对于需要数据的深度学习模型。
在这项工作中,我们集中在视觉检测的非监督缺陷分割。目标是在经过非缺陷样本的专门训练后,在图像中分割缺陷区域。已经证明基于卷积神经网络的架构如自动编码器或生成对抗网络可被用于此项任务。我们将在第2节简要介绍这些方法。这些模型试图在某些约束条件(如瓶颈)存在的情况下重构它们的输入,从而设法在低维空间中捕捉高维数据(如图像)的本质。假设测试数据中的异常偏离了训练数据流形,模型无法重现这些异常。因此,较大的重构误差表明存在缺陷。通常,所采用的误差度量是逐像素的 l p − l^p- lp−距离,这是为了简化和速度而做出的临时选择。然而,这些措施在重建只是轻微不准确的位置时产生高残差,例如,由于小的定位不精确的边缘。并且当输入图像和重建图像的像素的颜色值大致一致时,它们也无法检测出两者的结构差异。我们的研究表明,在复杂的现实场景中使用这种方法会限制其有效性。
为了缓解上述问题,我们建议使用结构相似度(SSIM)度量重建精度。SSIM是一种用于捕捉感知相似性的距离度量,它对边缘对齐不太敏感,并重视输入和重构之间的显著差异。它捕获局部像素区域之间的相互依赖关系,这些区域被当前最先进的基于自动编码器的无监督缺陷分割方法忽略。我们评估了在两个真实工业检测数据集上使用SSIM作为损失函数所获得的性能增益,并展示了相对于逐像素方法的显著性能增益。图1展示了纳米纤维材料NanoTWICE数据集上感知损失函数相对于逐像素 l 2 l^2 l2-损失的优势。尽管两个自动编码器都改变了有缺陷区域的重建,只有SSIM自动编码器的残差图允许对这些区域进行分割。在保持自动编码器结构不变,仅仅改变损失函数的情况下我们取得了与其他使用模型先验知识,如手工特征和预训练网络的最先进的无监督缺陷分割方法相近的表现。

2. Related Work
检测偏离训练数据的异常一直是机器学习中一个长期存在的问题。Pimentel等人(2014)对该领域进行了全面概述。在计算机视觉中,需要区分这一任务的两种变体。首先是分类场景,新样本作为完全不同的对象类别出现,应该作为异常值进行预测。其次,在一种情况下,异常表现为与已知结构的微妙偏差,需要对这些偏差进行分割。对于分类问题,已经提出了许多方法(Perera和Patel,2018;Sabokrou等人,2018)。在这里,我们将自己局限于试图解决后一个问题的方法的概述。
Napoletano等人(2018)从一个已经在分类任务上预先训练过的CNN中提取特征。在训练过程中,将特征聚类在字典中,当提取的特征强烈偏离学习的聚类中心时,识别异常结构。由于预训练网络可能无法提取出对当前新任务有用的特征,并且不清楚应该选择网络中的哪些特征进行聚类,因此该方法的普遍适用性不得到保证。使用这种方法获得的结果是NanoTWICE数据集上的最新技术,我们也在实验中使用了该数据集。他们改进了Carrera等人(2017)之前的结果,后者构建了一个字典,生成正常数据的稀疏表示。使用稀疏表示进行新颖性检测的类似方法有(Boracchi等人,2014;Carrera等人,2015,2016)。
Schlegl等人(2017)在视网膜的光学相干断层扫描图像上训练GAN,并通过搜索潜在样本来检测异常,如视网膜液,以最大限度地减少逐像素的 l 2 − l^2- l2−重建误差和鉴别器损失。为了找到合适的潜在样本而进行的大量的优化步骤使此方法非常的慢。因此,它只在时间不紧迫的应用程序中有用。最近,Zenati等人(2018)提出使用双向GANs (Donahue et al., 2017)添加缺失的编码器网络,以更快地进行推理。但是,GANs容易陷入模态崩溃,即不能保证无缺陷图像分布的所有模态都被模型捕获。此外,它们比自动编码器更难训练,因为对抗性训练的损失函数通常不能训练到收敛。训练结果必须在定期的优化间隔之后进行手动判断。
Baur等人(2018)提出了一个使用自编码架构和基于 l 1 − l^1- l1−距离的像素误差度量的缺陷分割框架。为了防止其损失函数的缺点,它们通过要求输入数据对齐和添加对抗损失来提高重建图像的视觉质量来提高重建质量。但是,对于许多处理非结构化数据的应用程序来说,不可能实现预先对齐。此外,在训练期间优化额外的对抗性损失,但在评估期间简单地基于逐像素比较分割缺陷可能会导致更糟糕的结果,因为不清楚对抗性训练如何影响重构。
其他方法考虑了变分自编码器(VAEs)的潜在空间结构,以定义异常值检测的测量。An和Cho(2015)通过从估计的编码分布中提取多个样本并测量解码输出的可变性,定义了每个图像像素的重构概率。Soukup和Pinetz(2018)完全不考虑解码器输出,而是计算KL散度,作为先验分布和编码器分布之间的新度量。这是基于这样一个假设,即有缺陷的输入将表现为与前一种输入非常不同的均值和方差。同样的,Vasilev等人(2018)定义了多种新颖性测度,要么纯粹考虑潜在空间行为或者将这些措施与逐像素重建损失相结合。它们获得一个指示异常的单个标量值,这可能很快成为分割场景中的性能瓶颈,在分割场景中,为了获得准确的分割结果,需要对每个图像像素进行单独的前向传递。我们表明,从VAEs获得的逐像素重建概率与逐像素确定性损失具有相同的问题。
上述所有使用自动编码器进行无监督缺陷分割的工作表明,自动编码器可靠地重建无缺陷图像,同时在视觉上改变有缺陷的区域,以保持重建接近训练数据的学习流形。然而,它们依赖于逐像素损失函数,使不现实的假设相邻像素值是相互独立的。我们表明,这防止这些方法从分割异常,主要是不同的结构,而不是像素强度。相反,我们建议使用SSIM (Wang et al., 2004)作为异常的损失函数和度量,通过比较输入和重构。SSIM考虑了局部斑块区域之间的相互依赖关系,通过计算局部斑块区域的一、二阶矩来模拟亮度、对比度和结构的差异。Ridgeway等(2015)研究表明,SSIM和密切相关的多尺度版本MS-SSIM (Wang et al., 2003)可以作为可微损失函数,在深度架构中生成更真实的图像,用于超分辨率等任务,但没有检查其在自动编码框架中用于缺陷分割的有效性。在我们所有的实验中,从逐像素到感知损失的转换在性能上有显著的提高,有时从完全失败的方法提高到令人满意的缺陷分割结果。
3. Methodology
3.1. Autoencoders for Unsupervised Defect Segmentation
自动编码器试图通过瓶颈结构将输入图像 x ∈ R k × h × w x \in \mathbb{R}^{k\times h\times w} x∈Rk×h×w映射到低维潜变量空间。自动编码器由一个编码方程 E : R k × h × w → R d E: \mathbb{R}^{k\times h\times w} \rightarrow\mathbb{R}^d E:Rk×h×w→Rd和一个解码方程 D : R d → R k × h × w D: \mathbb{R}^d\rightarrow\mathbb{R}^{k\times h\times w} D:Rd→Rk×h×w构成。其中, d d d表示潜空间维度, k , h , w k,h,w k,h,w分别表示输入图像的通道数、高和宽。选择 d ≪ k × h × w d\ll k\times h\times w d≪k×h×w以防止架构直接复制其输入,强迫编码器从输入图像提取有意义的特征来支持解码器对输入图像的准确重建。总体的流程可以总结为:
x ^ = D ( E ( x ) ) = D ( z ) \hat{x}=D(E(\bold{x}))=D(\bold{z}) x^=D(E(x))=D(z)
其中 z \bold{z} z是潜向量, x ^ \hat{\bold{x}} x^是输入的重建。在我们的实验中方程E和D由CNNs参数化。Strided Convolutions用于在编码器中对输入特征图进行下采样,在解码器中对输入特征图进行上采样。仅仅通过使用无缺陷图像数据进行训练自动编码器就能够用于无监督的缺陷分割任务。在测试过程中,自动编码器将无法重构训练过程中没有观察到的缺陷,因此可以通过比较原始输入与重构并计算残差图 R ( x , x ^ ) ∈ R w × h R(\bold{x},\bold{\hat{x}}) \in \mathbb{R^{w\times h}} R(x,x^)∈Rw×h来分割缺陷。
3.1.1. l 2 l^2 l2-Autoencoder
为了迫使自动编码器重构它的输入,必须定义一个损失函数来对它进行优化。为了简化和计算速度,人们经常选择逐像素误差度量,比如 l 2 l_2 l2损失
L 2 ( x , x ^ ) = ∑ r = 0 h − 1 ∑ c = 0 w − 1 ( x ( r , c ) − x ^ ( r , c ) ) 2 L_2(\bold{x}, \bold{\hat{x}})=\sum^{h-1}_{r=0}\sum^{w-1}_{c=0}(\bold{x(r,c)-\bold{\hat{x}}(r,c)})^2 L2(x,x^)=r=0∑h−1c=0∑w−1(x(r,c)−x^(r,c))2
其中, x ( r , c ) \bold{x(r,c)} x(r,c)表示图像 x \bold{x} x在像素 ( r , c ) (r,c) (r,c)处的强度值。为了在评估时获得残差图 R l 2 ( x , x ^ ) R_{l^2}(\bold{x}, \bold{\hat{x}}) Rl2(x,x^),需要计算 x , x ^ \bold{x}, \bold{\hat{x}} x,x^之间逐像素的 l 2 l^2 l2-距离。
3.1.2. Variational Autoencoder
确定性自动编码器框架的各种扩展都存在。VAEs对潜变量进行限制,使其遵循特定的分布 z ∼ P ( z ) \bold{z} \sim P(\bold{z}) z∼P(z)。为简单起见,通常选择分布为单位方差高斯分布。这就把整个框架变成了一个概率模型,它能够进行有效的后验推理,并允许从训练流形中通过从潜在分布采样生成新数据。通过编码输入图像获得的近似后验分布 Q ( z ∣ x ) Q(\bold{z}|\bold{x}) Q(z∣x)可以用来定义进一步的异常测量。一种选择是计算两个分布之间的距离,比如KL -散度 K L ( Q ( z ∣ x ) ∣ ∣ P ( z ) ) \mathcal{KL}(Q(\bold{z}|\bold{x})||P(\bold{z})) KL(Q(z∣x)∣∣P(z)),与先验分布 P ( z ) P(\bold{z}) P(z)偏差大的即为缺陷。然而,要使用这种方法对异常进行像素级的精确分割,必须对输入图像的每个像素执行单独的前向传递。第二种使用后验 Q ( z ∣ x ) Q(\bold{z}|\bold{x}) Q(z∣x)的方法是通过对从 Q ( z ∣ x ) Q(\bold{z}|\bold{x}) Q(z∣x)采样的N个潜变量 z 1 , z 2 , . . . , z N \bold{z}_1, \bold{z}_2, ..., \bold{z}_N z1,z2,...,zN进行解码产生一个空间残差图,并且按An和Cho(2015)提出的方法评估逐像素的重建概率 R V A E = P ( x ∣ z 1 , z 2 , . . . , z N ) R_{VAE}=P(\bold{x}|\bold{z}_1, \bold{z}_2, ..., \bold{z}_N) RVAE=P(x∣z1,z2,...,zN)。
3.1.3. Feature Matching Autoencoder
对标准自动编码器的另一个扩展是由Dosovitskiy和Brox(2016)提出的。它通过从输入图像 x \bold{x} x及其重构 x ^ \bold{\hat{x}} x^中提取特征并使它们相等来提高生成的重构的质量。考虑 F : R k × h × w → R f \mathit{F}: \mathbb{R}^{k\times h\times w}\rightarrow \mathbb{R}^f F:Rk×h×w→Rf是一个从输入图像提取 f \mathit{f} f-维特征向量的特征提取器。然后,可以在自编码器的损失函数中添加一个正则化器,产生特征匹配自编码器(FM-AE)损失
L F M ( x , x ^ ) = L 2 ( x , x ^ ) + λ ∣ ∣ F ( x ) − F ( x ^ ) ∣ ∣ 2 2 L_{FM}(\bold{x}, \bold{\hat{x}})=L_2(\bold{x}, \bold{\hat{x}})+\lambda ||F(\bold{x})-F(\bold{\hat{x}})||^2_2 LFM(x,x^)=L2(x,x^)+λ∣∣F(x)−F(x^)∣∣22
其中 λ > 0 \lambda > 0 λ>0是两个损失项的加权因子。 F \mathit{F} F可由在图像分类任务上预训练的CNN的第一层参数化。在评估阶段,通过比较 x \bold{x} x和 x ^ \bold{\hat{x}} x^的逐像素的 l 2 l^2 l2-距离得到残差图 R F M R_{FM} RFM。他们希望,与标准的 l 2 l^2 l2-autoencoder相比,更清晰、更真实的重建将带来更好的残差图。
3.1.4. SSIM Autoencoder
我们的研究表明,在无监督的缺陷分割任务中,使用更精细的架构,如VAEs或FM-AEs,与确定性的“ l 2 l^2 l2-自动编码器”相比,不能产生令人满意的残差图改进。它们都基于逐像素评估指标,假设相邻像素之间存在不切实际的独立性。因此,他们无法检测输入和重构之间的结构差异。通过调整损失和评估函数来捕获图像区域之间的局部相互依赖关系,我们能够大大改善上述所有架构。在第3.2节中,我们特别提出了结构相似性度量的使用 S S I M ( x , x ^ ) SSIM(\bold{x},\bold{\hat{x}}) SSIM(x,x^)作为损失函数和自编码器的评估度量,以获得残差映射 R S S I M R_{SSIM} RSSIM。
3.2. Structural Similarity
SSIM指数(Wang et al., 2004)定义了两个K × K图像patch p和q之间的距离度量,该度量考虑了他们在亮度 l ( p , q ) l(p,q) l(p,q),对比度 c ( p , q ) c(p,q) c(p,q)和结构 s ( p , q ) s(p,q) s(p,q)上的相似性:
S S I M ( p , q ) = l ( p , q ) α c ( p , q ) β s ( p , q ) γ ( 4 ) SSIM(p,q)=l(p,q)^\alpha c(p,q)^\beta s(p,q)^\gamma\space \space \space(4) SSIM(p,q)=l(p,q)αc(p,q)βs(p,q)γ (4)
其中, α , β , γ ∈ R \alpha, \beta, \gamma \in \mathbb{R} α,β,γ∈R是用户定义的常数用来加权三项。亮度测量 l ( p , q ) l(p,q) l(p,q)通过对比图像块的平均强度 μ p \mu_p μp和 μ q \mu_q μq进行。对比度测量 c ( p , q ) c(p,q) c(p,q)是图像块方差 σ p 2 \sigma^2_p σp2和 σ q 2 \sigma^2_q σq2的方程。结构测量 s ( p , q ) s(p,q) s(p,q)考虑两个图像块的协方差 σ p q \sigma_{pq} σpq。三项测量由下式定义:
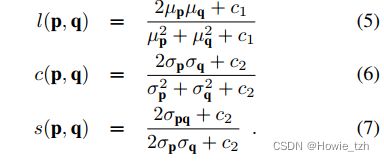
常量 c 1 c_1 c1和 c 2 c_2 c2保证数值稳定性,通常设为 c 1 = 0.01 c_1=0.01 c1=0.01, c 2 = 0.03 c_2=0.03 c2=0.03。将式(5)-(7)代入式(4):
S S I M ( p , q ) = ( 2 μ p μ q + c 1 ) ( 2 σ p q + c 2 ) ( μ p 2 + μ q 2 + c 1 ) ( σ p 2 + σ q 2 + c 2 ) ( 8 ) SSIM(p,q)=\frac{(2\mu_p\mu_q+c_1)(2\sigma_{pq}+c_2)}{(\mu^2_p+\mu^2_q+c_1)(\sigma^2_p+\sigma^2_q+c_2)} \space \space \space(8) SSIM(p,q)=(μp2+μq2+c1)(σp2+σq2+c2)(2μpμq+c1)(2σpq+c2) (8)
上式确保 S S I M ( p , q ) ∈ [ − 1 , 1 ] SSIM(p,q) \in [-1, 1] SSIM(p,q)∈[−1,1]。当且仅当 p p p和 q q q相同时, S S I M ( p , q ) = 1 SSIM(p,q)=1 SSIM(p,q)=1。图2显示了形成SSIM指数的三个相似函数的不同感知。:每一对图像块p和q都有一个恒定的 l 2 l^2 l2-残差为每像素0.25,因此这三种情况的缺陷评分都很低。另一方面,SSIM对各自残差图中patch的均值、方差和协方差的变化很敏感,在其中一个比较函数中,每个patch对的相似性都很低。

为了计算整个图像 x x x与其重构 x ^ \hat{x} x^之间的结构相似性,需要在图像上滑动一个K × K窗口,并在每个像素位置计算一个SSIM值。由于(8)是可微的,它可以被用作深度学习架构的损失函数,使用梯度下降进行优化。
图3显示了相对于像 l 2 l^2 l2这样的像素级误差函数,SSIM具有的优势。

对于 l 2 l^2 l2-距离,对边缘重建过程中的缺陷和不准确性在误差图中进行等量加权,使其无法区分。SSIM通过计算三种不同的统计特征进行图像比较,并对局部patch区域进行操作,在重建时对小的定位误差不太敏感。此外,它还能检测出结构变化而不是像素强度差异大的缺陷。对于添加在这个特殊玩具例子中的缺陷,对比度函数产生最大的残差。
4. Experiments
4.1. Datasets
由于缺乏工业场景中用于无监督缺陷分割的数据集,我们提供了两个机织织物纹理的新数据集,可向公众提供。我们为每个纹理提供100张无缺陷的图像,用于训练和验证,并提供50张包含各种缺陷的图像,如割伤、粗糙区域和织物上的污染。还为所有缺陷提供了像素精确的ground truth注释。所有图像大小为512 × 512像素,均为单通道灰度图像。缺陷和无缺陷纹理的例子可以在图4中看到。我们在纳米纤维材料数据集(Carrera et al., 2017)上进一步评估了我们的方法,该数据集包含5张大小为1024 × 700的无缺陷灰度图像,用于训练和验证,以及40张缺陷图像用于评估。图1显示了该数据集的示例图像。
