pytorch之参数的初始化

在训练神经网络模型的时候，权重的初始化十分重要，pytorch中提供了多种参数初始化的方法

初始化为某个常数

import torch
import torch.nn as nn
w = torch.empty(3, 5)
nw = nn.init.constant_(w, 0.2)
print(nw)

tensor([[0.2000, 0.2000, 0.2000, 0.2000, 0.2000],
        [0.2000, 0.2000, 0.2000, 0.2000, 0.2000],
        [0.2000, 0.2000, 0.2000, 0.2000, 0.2000]])

初始化为0

nw = nn.init.zeros_(w)
print(nw)

tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])

初始化为1

nw = nn.init.ones_(w)
print(nw)

tensor([[1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.]])

初始化为单位矩阵

nw = nn.init.eye_(w)
# 若w不是方阵，按照最小的维度处理
print(nw)

tensor([[1., 0., 0., 0., 0.],
        [0., 1., 0., 0., 0.],
        [0., 0., 1., 0., 0.]])

初始化为一个正交矩阵

nw = nn.init.orthogonal_(w)
print(nw)
print(torch.sum(nw[0] * nw[1]))
print(torch.sum(nw[0] * nw[0]))

tensor([[ 0.6990, -0.3041,  0.3926, -0.3489, -0.3783],
        [-0.3604, -0.3520,  0.3831,  0.5764, -0.5170],
        [ 0.2800,  0.6628, -0.2962,  0.2666, -0.5687]])
tensor(0.)
tensor(1.0000)

什么是正交矩阵, 可查看正交矩阵

初始化为稀疏矩阵

nw = nn.init.sparse_(w, sparsity=0.2)
print(nw)

tensor([[ 0.0274,  0.0000, -0.0034, -0.0059,  0.0000],
        [ 0.0000,  0.0112,  0.0000,  0.0000,  0.0093],
        [-0.0070,  0.0046, -0.0059, -0.0112,  0.0141]])

sparsity稀疏率为每一列被设置为0的占比，不为0的元素从正态分布$N(0,0.01)$中采样

初始化服从均匀分布$U(a,b)$, $a$,$b$是均匀分布的参数

nw = nn.init.uniform_(w, a=0.0, b=1.0)
print(nw)

tensor([[0.2483, 0.1599, 0.4203, 0.5972, 0.2742],
        [0.1345, 0.9816, 0.4995, 0.0487, 0.6926],
        [0.0484, 0.2419, 0.8147, 0.7584, 0.7443]])

初始化服从均匀分布$U(-a,a)$，但是均匀分布的参数$a$，通过计算得到

由论文Understanding the difficulty of training deep feedforward neural networks 提出，均匀分布的参数$a$:

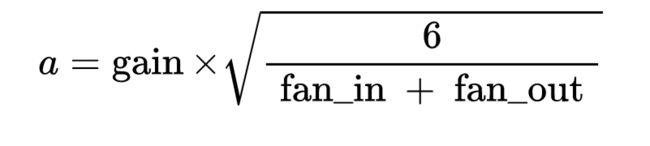
nw = nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('sigmoid'))
print(nw)

tensor([[-0.1168, -0.1941,  0.0650, -0.4598, -0.2400],
        [-0.3972,  0.3905, -0.3567,  0.5851, -0.5862],
        [-0.4050,  0.3008, -0.3010, -0.2625,  0.7496]])

由论文Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification 提出，均匀分布的参数$a$:

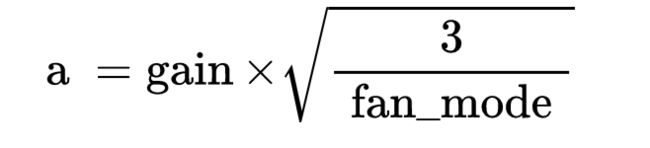
nw = nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')
print(nw)

tensor([[-0.9547,  0.6227,  0.7247, -0.8383, -0.2156],
        [ 0.5079, -0.6154, -1.0179,  0.9826, -0.2187],
        [ 0.0975, -1.0170,  0.2084,  0.1557,  0.4608]])

mode的取值可以是fan_in或者fan_out

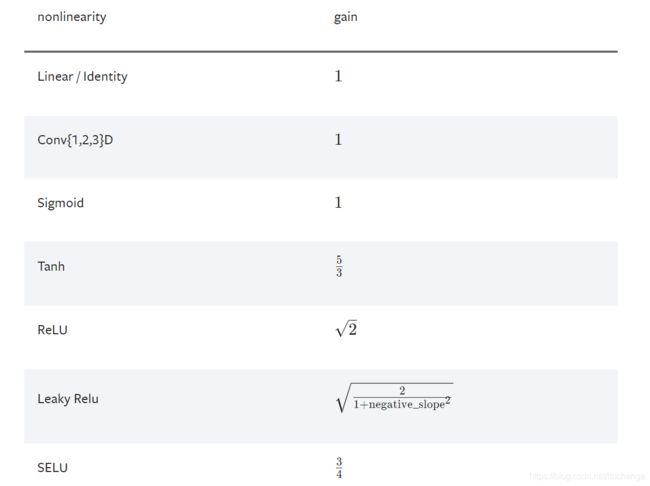
其中，gain为常数，可由nn.init.calculate_gain函数得到。nn.init.calculate_gain 对于不同的非线性函数有不同的增益值（有什么物理意义）。非线性函数及其对应的增益值如下图：

fan_in与fan_out通过输入tensor的维度得到，源代码如下

def _calculate_fan_in_and_fan_out(tensor):
    dimensions = tensor.dim()
    if dimensions < 2:
        raise ValueError("Fan in and fan out can not be computed for tensor with fewer than 2 dimensions")

    num_input_fmaps = tensor.size(1)
    num_output_fmaps = tensor.size(0)
    receptive_field_size = 1
    if tensor.dim() > 2:
        receptive_field_size = tensor[0][0].numel()
        # tensor.numel() 获取tensor中的元素个数
    fan_in = num_input_fmaps * receptive_field_size
    # fan_in 第二维 * receptive_field_size，上述例子为5
    fan_out = num_output_fmaps * receptive_field_size
    # fan_out 第一维 * receptive_field_size，上述例子为3
    return fan_in, fan_out

初始化服从正态分布分布,mean,std是正态分布的参数，代表均值和标准差

nw = nn.init.normal_(w, mean=0.0, std=1.0)
print(nw)

tensor([[-0.9467,  0.3426, -0.5911, -0.1969, -0.0165],
        [-1.4611, -0.4436, -1.0639, -0.4214,  1.8859],
        [-0.7308, -0.4682, -0.5144,  0.5951,  1.2855]])

初始化服从正态分布$N(0,st{d}^2)$，但是正态分布的标准差$std$，通过计算得到

由论文Understanding the difficulty of training deep feedforward neural networks 提出，正态分布的标准差$std$:

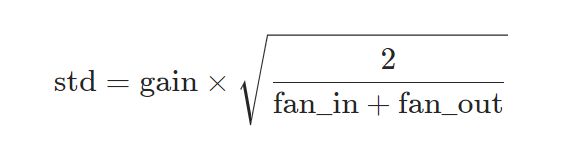
nw = nn.init.xavier_normal_(w, gain=1.0)
print(nw)

tensor([[ 0.7011, -0.2789,  0.3971,  0.2792, -0.0237],
        [-0.0708,  0.7436, -0.1604, -0.0242, -0.1682],
        [-0.1449,  0.0412,  0.5306,  0.9288, -0.0480]])

由论文Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification 提出，正态分布的标准差$std$:

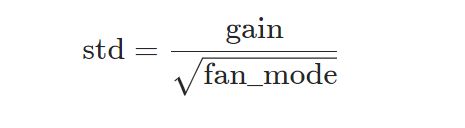
nw = nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')
print(nw)

tensor([[ 0.2741, -0.8150,  0.8118, -0.2063,  1.5686],
        [-0.3418,  1.0409,  0.2108, -0.3136,  0.9088],
        [-1.7762, -0.7985,  0.3178,  1.0679, -0.7122]])

翻译自pytorch官方文档