论文阅读《Adversarial Multiview Clustering Networks With Adaptive Fusion》

---

论文信息

论文标题：Adversarial Multiview Clustering Networks With Adaptive Fusion
论文作者：Qianqian Wang，Zhiqiang Tao，Wei Xia，Quanxue Gao，Xiaochun Cao，Licheng Jiao
论文来源： 2022，TNNLS
论文地址：download
论文代码：download

---

一、Abstract

挑战：现有的深度多视图聚类（MVC）方法主要基于自动编码器网络，该网络寻找公共潜在变量来分别重建每个视图的原始输入。然而，由于特定于视图的重建损失，在多个视图上提取一致的潜在表示以进行聚类是一个挑战。
AMvC概述：为了应对这一挑战，本文提出了对抗式MVC（AMvC）网络。所提出的AMvC根据不同视图之间的融合潜在表示生成每个视图的样本，以鼓励更一致的聚类结构。具体来说，使用多视图编码器从所有视图中提取潜在描述，并使用相应的生成器生成重构样本。将判别网络和均方损失联合用于训练多视图编码器和生成器，以平衡每个视图潜在表示的清晰度和一致性。此外，还提出了一种自适应融合层来获得共享的潜在表示，并在该层上施加了聚类损失和$l_{1,2}$-norm约束，以提高聚类性能和区分潜在空间。

二、Introduction

然而，现有的基于自动编码器的deep-MVC方法有一些局限性：
1） 它们仅利用重建损失来学习重建样本与原始样本之间的一致性信息，而重建损失是视图特有的，很难在多个视图上提取一致的潜在表示进行聚类。
2） 共享表示可能没有足够的区分能力进行聚类。
3） 这些方法中使用了各种融合方法，但它们忽略了不同的视图通常在重要性方面有所不同。

三、Adversarial Multiview Clustering Network

$l_{1,2}$-norm正则化使得共享潜在表示更容易区分。
我们构建了由三个子模块组成的AMvC网络：多视图编码器模块E、多视图生成对抗模块（包含生成器G和鉴别器D）和深度聚类模块（包含加权自适应融合层和深度嵌入聚类层）。

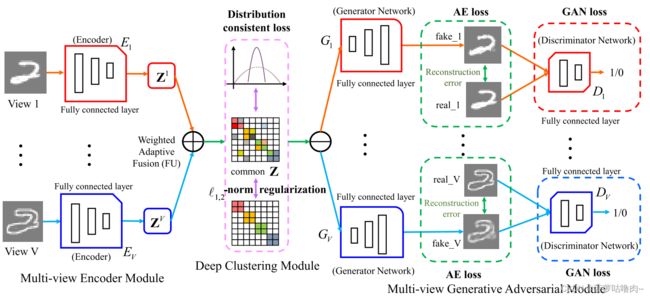
（一）多视图编码器模块

在多视图编码器网络$E=\left\{E_1,\dots ,E_v,\dots ,E_V\right\}$中，对于每个视图，都有M层独立的完全连接网络和N层完全连接的共享参数网络。独立图层用于处理每个视图的不同特征尺寸。对于$vth$视图$X^v$，编码器$E_v$旨在学习潜在表示${\mathbf{Z}}^v=\left\{z_1^{(v)},z_2^{(v)},\dots ,z_n^{(v)}\right\}\left({\mathbf{Z}}^v\in R^{m\times n}\right)$。具体而言，它将$d_v$维输入数据$x_i^{(v)}$映射到低维表示$z_i^{(v)}$。这个映射可以表示为${\mathbf{Z}}^v=E_v\left({\mathbf{X}}^v;{\theta }_{E_v}\right)$，$E_v$表示$vth$视图的编码网络，其参数为${\theta }_{E_v}$。

（二）多视图生成对抗模块

多视图生成器：$G=\left\{G_1,\dots ,G_v,\dots ,G_V\right\}$
多视图鉴别器：$D=\left\{D_1,\dots ,D_v,\dots ,D_V\right\}$
多视图生成器网络由具有共享参数的N层全连接网络和每个视图的M层独立全连接网络组成，可以生成所有视觉重建样本，并具有每个视图对应的潜在表示。
鉴别器网络由V个完全连接的层网络组成。每个鉴别器$D_v$由三个完全连接的层组成，我们应该注意，$x_i^{(v)}$是真实实例，而${\hat{x}}_i^{(v)}$是生成的样本。$D_v$将判别结果返回给生成器$G_v$，以更新其参数。通过这种方式，鉴别器作为正则化器来指导我们的多视点编码器网络E的训练，以提高嵌入表示的鲁棒性，并有效地解决过拟合问题。

（三）深度聚类模块

为了获得共享的潜在表示Z，我们在模型中引入了加权自适应融合层FU，它将V个潜在表示$Z_v$自适应地融合到公共表示$Z=f\left({\left\{Z^v\right\}}_{v=1}^V;\beta \right)$，$f(\cdot ;\beta )$表示融合函数。为了寻找一个聚类友好的潜在空间，我们在网络中开发了一个独特的深度嵌入聚类层$CU$。嵌入的聚类层在每次迭代后都包含新的聚类质心。我们使用共享表示Z和簇质心${\left\{{\mu }_j\right\}}_{j=1}^k$来获得当前数据分布和目标数据分布。此外，我们利用当前数据分布和目标数据分布的$Kullback–Leibler(KL)$散度作为目标函数，迭代更新共享表示Z和簇质心${\left\{{\mu }_j\right\}}_{j=1}^k$。

（四）总体目标函数

$$\underset{E,G,\beta ,\mu }{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{A}\mathrm{E}}+{\lambda }_1{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}+{\lambda }_2{\mathcal{L}}_{\mathrm{C}\mathrm{L}\mathrm{U}}+{\lambda }_3{\mathcal{L}}_{12}$$
包括四个部分：自动编码器（AE）损失，GAN损失，聚类损失CLU，1,2-范数正则化。
${\mathcal{L}}_{\mathrm{A}\mathrm{E}}={\sum }_{v=1}^V{\Vert {\mathbf{X}}^v-{\hat{\mathbf{X}}}^v\Vert }_{\mathrm{F}}^2$

${\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}={\sum }_{v=1}^V\left({\mathbb{E}}_{x^v\sim P\left({\mathbf{X}}^v\right)}\left[\log D_v\left(x^v\right)\right]+{\mathbb{E}}_{{\hat{x}}^v\sim P\left({\hat{\mathbf{X}}}^v\right)}\left[\log \left(1-D_v\left({\hat{x}}^v\right)\right)\right]\right)$
实际数据分布和生成的数据分布

$\mathbf{Z}=f\left({\left\{{\mathbf{Z}}^v\right\}}_{v=1}^V;\beta \right)={\sum }_{v=1}^V{\beta }_v{\mathbf{Z}}^v/{\sum }_{v=1}^V{\beta }_v$

${\mathcal{L}}_{\mathrm{C}\mathrm{L}\mathrm{U}}={\sum }_i{\sum }_j{p}_{ij}\log \frac{p_{ij}}{q_{ij}}$

${\mathcal{L}}_{12}=\Vert {\mathbf{Z}|}_{1,2}=\sqrt{{\sum }_i{\left({\sum }_j\left|z_{ij}\right|\right)}^2}$

（五）算法伪代码