【动手学深度学习】用多项式回归来探索过拟合、欠拟合的概念(含源代码)
目录:多项式回归
- 一、多项式回归的具体实现步骤
-
- 1.1 导包
- 1.2 生成数据集
- 1.3 对模型进行训练和测试
- 1.4 三阶多项式函数拟合(正常)
- 1.5 线性函数拟合(欠拟合)
- 1.6 高阶多项式函数拟合(过拟合)
- 二、源代码
一、多项式回归的具体实现步骤
1.1 导包
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
1.2 生成数据集
给定 x x x,我们将使用以下三阶多项式来生成训练和测试数据的标签:
y = 5 + 1.2 x − 3.4 x 2 2 ! + 5.6 x 3 3 ! + ϵ ( w h e r e ) ϵ ∈ N ( 0 , 0.0 1 2 ) y=5+1.2x-3.4\frac{x^2}{2!}+5.6\frac{x^3}{3!}+\epsilon (where)\quad \quad \epsilon \in N(0, 0.01^2) y=5+1.2x−3.42!x2+5.63!x3+ϵ(where)ϵ∈N(0,0.012)
噪声项 ϵ \epsilon ϵ服从均值为0且标准差为0.1的正态分布。在优化的过程中,我们通常希望避免非常大的梯度值或损失值。这就是我们将特征从 x i x^i xi调整为 x i i ! \frac{x^i}{i!} i!xi的原因,这样可以避免很大的 i i i带来的特别大的指数值。我们将为训练集和测试集各生成100个样本。
max_degree = 10 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练和测试数据集的大小
true_w = np.zeros(max_degree)
true_w[0 : 4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size = (n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale = 0.1, size = labels.shape)
true_w, features, poly_features, labels = [torch.tensor(x, dtype = torch.float32) for x in [true_w, features, poly_features, labels]]
我们展示一下生成的样本:
(PyTorch) D:\Code Project>D:/Anaconda/envs/PyTorch/python.exe "d:/Code Project/15.动手学深度学习代码手撸/多项式回归.py"
tensor([ 5.0000, 1.2000, -3.4000, 5.6000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000]) tensor([[-5.8204e-01],
[-4.1354e-01],
[-1.3842e+00],
[ 1.2165e+00],
[-9.3619e-01],
[ 1.0103e+00],
[-2.3114e+00],
[ 9.7913e-01],
[-1.2603e+00],
[-9.3715e-01],
[ 6.9850e-01],
[-8.5771e-01],
[ 7.7881e-02],
[ 3.3513e-01],
[-4.2389e-01],
[-1.5797e+00],
[ 1.4692e+00],
[-7.2698e-01],
[-1.1640e+00],
[-6.0994e-02],
[ 6.1747e-01],
[ 1.2974e+00],
[ 5.4491e-01],
[ 1.7164e-01],
[-1.0237e+00],
[-1.4641e-01],
[ 5.9836e-02],
[ 2.5196e-01],
[-1.2384e+00],
[ 2.5462e+00],
[ 8.1987e-01],
[ 1.1473e+00],
[ 7.0152e-01],
[ 2.4810e+00],
[ 7.7851e-02],
[-8.3684e-01],
[-3.1834e-01],
[ 5.9410e-01],
[-2.2319e-01],
[-7.5866e-01],
[ 1.0995e+00],
[ 6.2042e-01],
[ 8.3782e-01],
[-9.3573e-01],
[ 7.5042e-01],
[ 1.2749e-01],
[ 8.6680e-01],
[ 2.8337e-01],
[-9.1962e-01],
[-1.2623e-01],
[-6.4161e-01],
[ 2.6536e-01],
[ 4.2738e-03],
[-7.0316e-01],
[-4.5810e-01],
[-2.3423e+00],
[-1.6232e-01],
[-2.3610e+00],
[-7.3811e-01],
[-1.6048e+00],
[ 2.5226e-01],
[ 3.0043e-01],
[ 1.5431e-01],
[ 9.3174e-03],
[ 9.5100e-01],
[-3.7268e-01],
[ 5.9177e-01],
[ 7.0089e-01],
[-1.7181e+00],
[ 2.6630e-01],
[-1.3438e+00],
[-7.6255e-01],
[ 2.6089e-01],
[-1.5181e+00],
[ 1.7126e-02],
[-5.1383e-02],
[ 1.3159e-01],
[-2.5283e+00],
[-2.1622e-01],
[-8.9613e-01],
[-4.0597e-01],
[ 2.3240e-01],
[-1.8934e+00],
[ 4.5945e-01],
[ 5.8147e-01],
[ 6.1098e-01],
[ 7.1349e-01],
[ 4.9356e-01],
[ 3.1397e-01],
[ 6.2009e-01],
[ 1.1873e+00],
[ 9.4851e-01],
[ 4.4866e-01],
[-5.5612e-01],
[-5.4590e-01],
[ 1.1263e-01],
[ 8.1760e-01],
[ 1.7099e-03],
[-4.4908e-01],
[ 1.7569e+00],
[ 6.2862e-01],
[-2.1252e+00],
[-6.0591e-01],
[-1.2537e+00],
[-7.8645e-01],
[-1.0066e+00],
[-6.8334e-01],
[-1.2359e+00],
[ 1.3371e+00],
[ 1.0041e+00],
[-1.6308e+00],
[ 2.8751e-01],
[-5.7340e-01],
[-6.2660e-01],
[-4.1243e-01],
[ 2.3550e-01],
[-1.2430e+00],
[-7.4530e-01],
[-2.5342e-01],
[ 9.2844e-03],
[ 1.2422e+00],
[ 9.1148e-01],
[-6.1099e-01],
[-1.1701e-01],
[ 8.7528e-01],
[ 2.2408e-01],
[ 6.1080e-01],
[-6.8568e-01],
[ 9.5865e-01],
[-3.3298e-01],
[ 4.6232e-01],
[ 1.4067e+00],
[ 9.5124e-01],
[ 5.8045e-01],
[ 1.0532e+00],
[ 6.9557e-02],
[ 5.5788e-01],
[ 9.3110e-01],
[-2.0058e-01],
[ 5.1956e-01],
[ 1.0500e+00],
[-2.1085e-01],
[-9.6234e-01],
[-2.7142e-01],
[-1.8670e-01],
[ 4.0889e-01],
[-7.6292e-02],
[ 4.4040e-01],
[ 7.2167e-01],
[-4.9551e-01],
[-4.1760e-01],
[ 4.5403e-01],
[-1.0109e+00],
[ 1.0923e+00],
[-5.5266e-01],
[-1.1013e+00],
[ 2.8899e-01],
[-1.2559e+00],
[ 4.3337e-01],
[ 8.6826e-02],
[ 1.1728e+00],
[-8.3035e-02],
[-1.6254e+00],
[ 3.1177e-01],
[ 4.6349e-01],
[ 1.7947e-01],
[-2.7928e+00],
[ 7.0044e-01],
[-4.3124e-01],
[ 5.6083e-01],
[-1.5352e+00],
[-1.5788e-01],
[ 4.9791e-01],
[-3.8145e-01],
[ 7.4795e-01],
[ 1.5549e-01],
[-1.2756e+00],
[ 1.2751e+00],
[-8.1178e-01],
[-5.8266e-01],
[-5.3529e-01],
[-1.1328e+00],
[-1.8097e+00],
[-1.1646e+00],
[ 8.2900e-01],
[-7.1854e-01],
[-1.6269e-01],
[-9.1055e-01],
[ 3.9561e-01],
[ 1.8351e+00],
[-3.0961e-01],
[-7.3661e-01],
[ 2.8203e-01],
[ 2.6192e-01],
[-1.4871e+00],
[-6.2431e-01],
[ 1.6839e-02],
[-2.0540e+00],
[ 5.9307e-01],
[-1.4603e-01]]) tensor([[ 1.0000e+00, -5.8204e-01, 1.6938e-01, ..., -4.4897e-06,
3.2665e-07, -2.1125e-08],
[ 1.0000e+00, -4.1354e-01, 8.5508e-02, ..., -4.1040e-07,
2.1214e-08, -9.7478e-10],
[ 1.0000e+00, -1.3842e+00, 9.5799e-01, ..., -1.9317e-03,
3.3423e-04, -5.1404e-05],
...,
[ 1.0000e+00, -2.0540e+00, 2.1095e+00, ..., -3.0607e-02,
7.8585e-03, -1.7935e-03],
[ 1.0000e+00, 5.9307e-01, 1.7586e-01, ..., 5.1202e-06,
3.7958e-07, 2.5013e-08],
[ 1.0000e+00, -1.4603e-01, 1.0662e-02, ..., -2.8094e-10,
5.1281e-12, -8.3205e-14]]) tensor([ 3.4885e+00, 4.0917e+00, -2.3288e+00, 5.3935e+00, 1.6003e+00,
5.3897e+00, -1.8491e+01, 5.5361e+00, -1.0447e+00, 1.6086e+00,
5.3370e+00, 2.1585e+00, 4.9845e+00, 5.1793e+00, 4.0552e+00,
-4.8727e+00, 6.0244e+00, 2.8781e+00, -6.1735e-04, 5.0134e+00,
5.3642e+00, 5.7554e+00, 5.3119e+00, 5.2375e+00, 9.5282e-01,
4.6951e+00, 5.0728e+00, 5.1920e+00, -8.8672e-01, 1.2431e+01,
5.4061e+00, 5.6446e+00, 5.2314e+00, 1.1599e+01, 5.0794e+00,
2.1780e+00, 4.4197e+00, 5.5348e+00, 4.6503e+00, 2.7133e+00,
5.4676e+00, 5.4266e+00, 5.3636e+00, 1.4944e+00, 5.4712e+00,
5.2786e+00, 5.3801e+00, 5.2232e+00, 1.8191e+00, 4.8260e+00,
3.3381e+00, 5.2327e+00, 4.9527e+00, 2.9454e+00, 4.0103e+00,
-1.9060e+01, 4.9773e+00, -1.9623e+01, 2.6554e+00, -5.1475e+00,
5.1305e+00, 5.2740e+00, 4.9878e+00, 5.0633e+00, 5.1281e+00,
4.2693e+00, 5.3263e+00, 5.2312e+00, -6.8813e+00, 5.0425e+00,
-1.9981e+00, 2.7128e+00, 5.2563e+00, -3.9199e+00, 5.1426e+00,
4.9214e+00, 5.2561e+00, -2.4005e+01, 4.5385e+00, 1.9128e+00,
4.1308e+00, 5.3363e+00, -9.6458e+00, 5.2746e+00, 5.3650e+00,
5.3426e+00, 5.3519e+00, 5.3885e+00, 5.1409e+00, 5.1814e+00,
5.8153e+00, 5.2205e+00, 5.2991e+00, 3.5891e+00, 3.6678e+00,
5.3750e+00, 5.3385e+00, 4.8676e+00, 4.0784e+00, 6.8247e+00,
5.3681e+00, -1.4193e+01, 3.4357e+00, -1.0679e+00, 2.6203e+00,
1.0419e+00, 3.2584e+00, -9.2814e-01, 5.9517e+00, 5.5835e+00,
-5.6508e+00, 5.0926e+00, 3.6303e+00, 3.4880e+00, 4.2027e+00,
5.1795e+00, -8.7564e-01, 2.6951e+00, 4.5564e+00, 5.0955e+00,
5.6504e+00, 5.3790e+00, 3.5358e+00, 4.7344e+00, 5.2101e+00,
5.0880e+00, 5.3413e+00, 3.1594e+00, 5.3250e+00, 4.3693e+00,
5.2838e+00, 5.9421e+00, 5.3943e+00, 5.3115e+00, 5.5559e+00,
5.1860e+00, 5.2793e+00, 5.5494e+00, 4.4732e+00, 5.3140e+00,
5.5291e+00, 4.5108e+00, 1.3570e+00, 4.5473e+00, 4.6032e+00,
5.3831e+00, 4.9449e+00, 5.1396e+00, 5.5503e+00, 3.9743e+00,
4.1499e+00, 5.1417e+00, 1.3329e+00, 5.4652e+00, 3.5364e+00,
5.0843e-01, 5.0991e+00, -1.1198e+00, 5.3471e+00, 5.1166e+00,
5.5840e+00, 4.7595e+00, -5.5959e+00, 5.2216e+00, 5.2718e+00,
5.2305e+00, -3.1953e+01, 5.3284e+00, 4.1471e+00, 5.2740e+00,
-4.3089e+00, 4.8549e+00, 5.3629e+00, 4.1681e+00, 5.2186e+00,
5.1821e+00, -1.2452e+00, 5.7531e+00, 2.3379e+00, 3.4589e+00,
3.8644e+00, 2.0462e-01, -8.2135e+00, -1.8192e-01, 5.2461e+00,
2.8457e+00, 4.8033e+00, 1.7397e+00, 5.2114e+00, 7.2266e+00,
4.4511e+00, 2.6207e+00, 5.0074e+00, 5.2234e+00, -3.6819e+00,
3.3239e+00, 5.0024e+00, -1.2873e+01, 5.3138e+00, 4.6746e+00])
它们分别对应的数据维度为:
(PyTorch) D:\Code Project>D:/Anaconda/envs/PyTorch/python.exe "d:/Code Project/15.动手学深度学习代码手撸/多项式回归.py"
torch.Size([10]) torch.Size([200, 1]) torch.Size([200, 10]) torch.Size([200])
同样,存储在poly_features中的单项式由gamma函数重新缩放, 其中 g a m m a ( n ) = ( n − 1 ) ! gamma(n) = (n - 1)! gamma(n)=(n−1)!。
1.3 对模型进行训练和测试
首先让我们实现一个函数来评估模型在给定数据集上的损失。
def evaluate_loss(net, data_iter, loss):
metric = d2l.Accumulator(2) # 损失的总和,样本数量
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
现在定义训练函数:
def train(train_features, test_features, train_labels, test_labels, num_epochs = 400):
loss = nn.MSELoss(reduction='none')
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape, 1, bias = False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)), batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)), batch_size)
trainer = torch.optim.SGD(net.parameters(), lr = 0.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log', xlim=[1, num_epochs], ylim=[1e-3, 1e2], legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss), evaluate_loss(net, test_iter, loss)))
print('weight:', net[0].weight.data.numpy())
d2l.plt.show()
1.4 三阶多项式函数拟合(正常)
我们将首先使用三阶多项式函数,它与数据生成函数的阶数相同。 结果表明,该模型能有效降低训练损失和测试损失。 学习到的模型参数也接近真实值 ω = [ 5 , 1.2 , − 3.4 , 5.6 ] \omega=[5,1.2,-3.4,5.6] ω=[5,1.2,−3.4,5.6]。
从多项式特征中选择前4个维度,即1, x x x, x 2 2 ! \frac{x^2}{2!} 2!x2, x 3 3 ! \frac{x^3}{3!} 3!x3。
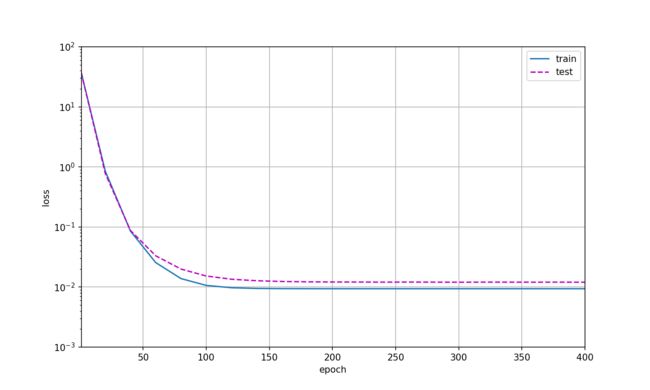
此时的权重值为:
weight: [[ 5.003262 1.2241048 -3.4129844 5.5369105]]
我们得到的方程为:
y = 5.003262 + 1.2241048 x − 3.4129844 x 2 2 ! + 5.5369105 x 3 3 ! y=5.003262+1.2241048x-3.4129844\frac{x^2}{2!}+5.5369105\frac{x^3}{3!} y=5.003262+1.2241048x−3.41298442!x2+5.53691053!x3
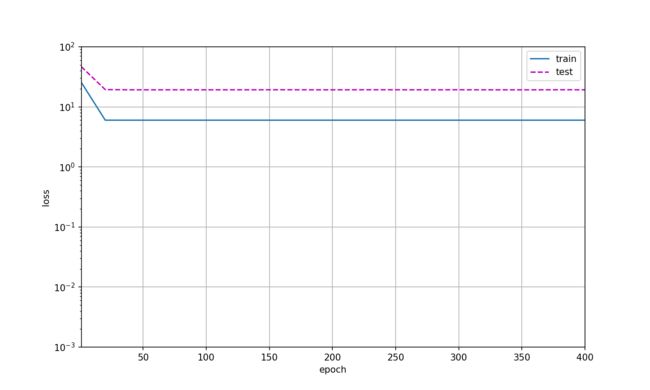
1.5 线性函数拟合(欠拟合)
让我们再看看线性函数拟合,减少该模型的训练损失相对困难。 在最后一个迭代周期完成后,训练损失仍然很高。 当用来拟合非线性模式(如这里的三阶多项式函数)时,线性模型容易欠拟合。
weight: [[3.35787 3.4704547]]
我们得到的方程为:
y = 3.35787 + 3.4704547 x y=3.35787+3.4704547x y=3.35787+3.4704547x
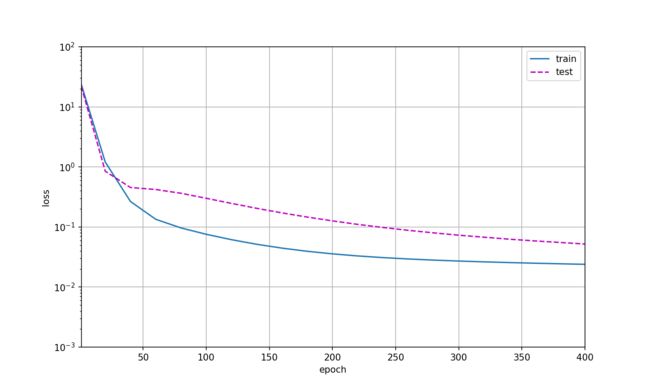
1.6 高阶多项式函数拟合(过拟合)
现在,让我们尝试使用一个阶数过高的多项式来训练模型。 在这种情况下,没有足够的数据用于学到高阶系数应该具有接近于零的值。 因此,这个过于复杂的模型会轻易受到训练数据中噪声的影响。 虽然训练损失可以有效地降低,但测试损失仍然很高。 结果表明,复杂模型对数据造成了过拟合。
weight: [[ 4.926031 1.3673187 -2.989791 4.8871026 -1.2988803 1.0961614
-0.14757498 0.17588839 0.25481126 0.14741105]]
二、源代码
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
def evaluate_loss(net, data_iter, loss):
metric = d2l.Accumulator(2) # 损失的总和,样本数量
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
def train(train_features, test_features, train_labels, test_labels, num_epochs = 400):
loss = nn.MSELoss(reduction='none')
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape, 1, bias = False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)), batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)), batch_size)
trainer = torch.optim.SGD(net.parameters(), lr = 0.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log', xlim=[1, num_epochs], ylim=[1e-3, 1e2], legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss), evaluate_loss(net, test_iter, loss)))
print('weight:', net[0].weight.data.numpy())
d2l.plt.show()
if __name__ == '__main__':
max_degree = 10 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练和测试数据集的大小
true_w = np.zeros(max_degree)
true_w[0 : 4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size = (n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale = 0.1, size = labels.shape)
true_w, features, poly_features, labels = [torch.tensor(x, dtype = torch.float32) for x in [true_w, features, poly_features, labels]]
print(true_w.shape, features.shape, poly_features.shape, labels.shape)
train(poly_features[:n_train, :], poly_features[n_train:, :], labels[:n_train], labels[n_train:])