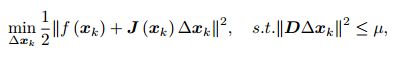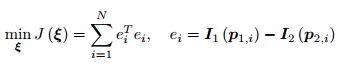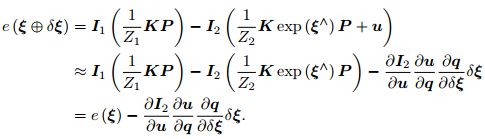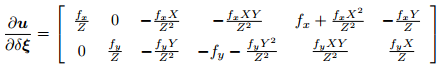G2O 图优化基础与示例汇总

        在汇总图优化相关知识时，我们知道图优化模型主要是使用g2o进行代码编程。看见《SLAM》P123页时，有4个步骤/

1. 定义顶点和边的类型；
2. 构建图；
3. 选择优化算法；
4. 调用g2o进行优化，返回结果。

        本文针对经常遇到的g2o示例进行汇总，试图总结g2o的常用编程套路和最小化残差模型的建模套路。

附：高斯牛顿法GN优化步骤：

        它的思想是将f(x)进行一阶泰勒展开：

1. 给定初值x0；

2. 对于第k次迭代，求出当前的雅克比矩阵J(x_k)和误差f(x_k)；

3. 求解增量方程：H△ = g；

4. 若△足够小，则停止；否则，令 =  + △，返回第2步。

        LM定义比例因子表示近似模型和实际函数之间的差异：

 

步骤如下：

1. 给定初值x0，以及初始优化半径μ；

2. 对于第k次迭代，求解：

μ是信赖区域的半径。D可以是单位阵，相当于将△x约束在球中；D也可以是非负数对角阵——（实际中通常用的对角元素的平方根，使得在梯度小的维度上约束范围更大一些。）

3. 计算ρ。

4. 若ρ>3/4，则μ = 2μ。

5. 若ρ<1/4，则μ = 0.5μ。

6. 如果ρ大于某阈值，则认为近似可行。 令 =  + △ 。

7. 判断算法是否收敛，如不收敛则返回第2步，否则结束。

 

1、g2o编程常用步骤

        老样子，还是先总结g2o的编程套路：

        0. 定义块维度

typedef g2o::BlockSolver< g2o::BlockSolverTraits<6, 3> > Block;  
// pose维度为6，landmark维度为3

        1. 创建一个线性方程求解器LinearSolver；

        2. 创建BlockSolver，并用上面定义的线性求解器初始化；

        3. 创建总求解器solver，并从GN、LM、DogLeg中选一个，再用上述求解器BlockSolver初始化；

        4. 创建稀疏求解器；

        5. 定义图中的顶点和边；

        6. 设置优化参数，开始执行优化。

2、顶点的相关函数

        1. 读盘和存盘函数：

virtual bool read(istream& in) {}
virtual bool write(ostream& out) const {}

        2. 顶点的更新函数oplusImpl。优化过程最重要的就是增量△x的计算，本函数就是处理  =  + △ 的过程。  

        3. 顶点的重置函数setToOriginImpl。把估计值置零即可。

2.1 曲线拟合中的顶点

        ch6/g2o_curve_fitting中使用的曲线模型顶点是：

// 第5步：定义图的顶点和边，并往图中添加顶点
CurveFittingVertex* v = new CurveFittingVertex();    // 设置顶点
v->setEstimate( Eigen::Vector3d(0,0,0) );   // 设置估计值，这里相当于对待优化量abc没有初始估计值
v->setId(0);    // 编号
optimizer.addVertex( v );    // 往图中添加顶点

        顶点定义如下，这里基于原生的g2o::BaseVertex<3, Eigen::Vector3d>进行重写：

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    // 重置，估计系数（待优化的系数）重写虚函数
    // override保留字表示当前函数重写了基类的虚函数
    virtual void setToOriginImpl()  // 重置
    {
        _estimate << 0, 0, 0;       // 设置估计的系数
    }

    // 更新估计系数（待优化的系数）重写虚函数
    virtual void oplusImpl( const double* update )  // 更新
    {
        _estimate += Eigen::Vector3d(update);
    }

    // 存盘和读盘：留空
    virtual bool read( istream& in )  {  }
    virtual bool write( ostream& out ) const {  }
};

        

2.2 PnP中的重投影顶点定义

        用的是两种g2o中原生的顶点，其中位姿顶点用的是g2o::VertexSE3Expmap()顶点，路标点（三维空间点）用的是g2o::VertexSBAPointXYZ()。位姿顶点定义如下：

g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap();    // camera pose，李代数位姿节点
Eigen::Matrix3d R_mat;      // 注意CV中的矩阵与Eigen中的矩阵相互转换
R_mat <<
        R.at (0,0), R.at (0,1), R.at (0,2),
        R.at (1,0), R.at (1,1), R.at (1,2),
        R.at (2,0), R.at (2,1), R.at (2,2);

pose->setId(0);
pose->setEstimate( g2o::SE3Quat(
                        R_mat,
                        Eigen::Vector3d( t.at(0,0), t.at(1,0), t.at(2,0) )
                 ) );
// 定义相机位姿使用SE3Quat，这个类内部使用四元数加位移向量来存储位姿
optimizer.addVertex( pose );

        路标点顶点定义如下：

int index = 1;
for ( const Point3f p:points_3d )   // landmarks，第一幅图坐标系下的三维空间点
{
    g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
    point->setId( index ++ );
    point->setEstimate( Eigen::Vector3d( p.x, p.y, p.z ) );
    point->setMarginalized( true );     // g2o中必须设置marg参见第10讲内容
    optimizer.addVertex( point );
}

2.3 稀疏直接法和半稠密直接法中的顶点定义

        用的都是原生的g2o顶点：

// 第五步：设置顶点和边
// 设置第0个顶点
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap();
pose->setEstimate ( g2o::SE3Quat ( Tcw.rotation(), Tcw.translation() ) );   // 设置Tcw变换位姿初值
pose->setId ( 0 );
optimizer.addVertex ( pose );

3、边的相关函数

        1. 读盘和存盘函数：

virtual bool read(istream& in) { }
virtual bool write(ostream& out) const {}

        2. 残差计算函数 computeError()，计算残差e()，也就是上面的f(x)。

        3. 计算雅可比矩阵，计算。

        要想写出边的以上几个主要函数，首先要将整个问题参数化（或者说建模），然后进行数学推导。以《SLAM 14讲》中下面几个例子说明：

3.1 曲线拟合的边

        ch6曲线拟合中也基于原生的g2o::BaseUnaryEdge<1, double, CurveFittingVertex>进行了重写，这里记录下参数意义，1表示残差维度，double表示残差类型，CurveFittingVertex表示与边相连的顶点类型，这里只连接一个前面自定义的Curve顶点类型。

代码如下：

// 误差模型(边) 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1, double, CurveFittingVertex>
{
public:
    double _x;      // x值，y值为_measurement

public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x ) : BaseUnaryEdge(), _x(x) { }

    // 计算曲线模型误差
    void computeError()
    {
        const CurveFittingVertex* v = static_cast (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();      // abc待优化的系数
        // 误差函数 =y-exp(ax2+bx+c)  这里面的abc都是待优化的系数
        _error(0, 0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) );
    }

    // 存盘和读盘：留空
    virtual bool read( istream& in )   { }
    virtual bool write( ostream& out ) const {  }
};

3.2 PnP中的重投影优化的边

        

3.3 直接法中的光度误差优化的边

       在推导直接法光度误差时，先明白直接法和特征点法的区别：

        1. 直接法保留特征点，但只计算关键点，不计算描述子。使用光流法（Optical Flow）来跟踪特征点的运动。避免计算和匹配描述子的计算过程，但光流本身需要时间。

        2. 只计算关键点，不计算描述子。使用直接法（Direct Method）来计算特征点在下一时刻图像中的位置。 这也就是下面要推导的直接法的思路。稀疏直接法。

        3. 既不计算关键点，也不计算描述子，根据像素灰度的差异，直接计算相机运动。半稠密直接法和稠密直接法。

        考虑某个空间点P和两个时刻的相机。P的坐标为[X, Y, Z]（第一帧的相机坐标系下的描述），它在两个相机上的成像，记非齐次坐标为和。

        我们的目标是求第一个相机到第二个相机的相对位姿变换。

其中  是 P 的深度，  是 P 在第二个相机坐标系下的深度，也就是 RP + t 的第三个
坐标值。由于 exp(ξ^) 只能和齐次坐标相乘，所以我们乘完之后要取出前三个元素。这和
上一讲以及相机模型部分的内容是一致的。 

       

        特征点法：通过匹配描述子，知道p1和p2的像素位置，可以计算重投影误差。

        直接法：没有特征匹配，无法知道p1和p2的对应关系。直接法的思路是根据当前相机的位姿估计值，来寻找p2的位置。但若相机的位姿不够好，p1和p2会有明显的差别。通过优化相机位姿，最小化的是光度误差（Photometric Error），也就是P的两个像素的亮度误差：

        光度误差的基本假设是灰度不变假设。在直接法中，我们假设一个空间点在各个视角下，成像的灰度是不变的。我们有许多个（比如 N 个）空间点 Pi，那么，整个相机位姿估计问题变为：

        注意这里的优化变量是相机位姿 ξ。为了求解这个优化问题，我们关心误差 e 是如何随着相机位姿 ξ 变化的，需要分析它们的导数关系。因此，使用李代数上的扰动模型。我们给 exp(ξ) 左乘一个小扰动 exp(δξ)，得： 

        这里的 q 为 P 在扰动之后，位于第二个相机坐标系下的坐标，而 u 为它的像素坐标。利用一阶泰勒展开，有：

一阶导数由于链式法则分成了三项，而这三项都是容易计算的：

        1.  为 u 处的像素梯度；

        2. 为投影方程关于相机坐标系下的三维点的导数。记 q = ，根据上一节的推导，导数为：

        3.   为变换后的三维点对变换的导数，这在李代数章节已经介绍过了：

        在实践中，由于后两项只与三维点 q 有关，而与图像无关，我们经常把它合并在一起：

        这个 2 × 6 的矩阵在上一讲中也出现过。于是，我们推导了误差相对于李代数的雅可
比矩阵：

至此，推导部分结束，代码部分如下：

 

 

 

 

 

3.4 后端g2o优化数据集中的边

 

参考博客：

1、https://zhaoxuhui.top/blog/2018/04/10/g2o&bundle_adjustment.html#2g2o%E5%BA%93%E7%AE%80%E4%BB%8B%E4%B8%8E%E7%BC%96%E8%AF%91%E5%AE%89%E8%A3%85 G2O图优化基础和SLAM的Bundle Adjustment(光束法平差)