python数据挖掘课程设计——基于数据挖掘的森林火灾预测分析（数据代码+数据分析+数据可视化展示）

基于数据挖掘的森林火灾预测分析

[摘要]随着全球范围性的温室效应，全球气温正逐步升高，为对抗温室效应，森林已经成为我们急需保护的资源，但是火灾时刻威胁着森林资源。为了帮助对抗温室效应、保护森林，本研究通过选取葡萄牙蒙特西尼奥自然公园的 517 起火灾的记录，采用数据挖掘技术对数据进行聚类分析、线性回归分析等操作，得到火灾发生的主要因素，最终为林业管理者预测森林火灾发生、森林火灾管控、降低人员财产损失等方面提供相关建议，具有较高的经济价值和学术价值。

[关键字]：数据挖掘 森林火灾 回归预测

第一章 前言

森林火灾是森林生态系统天敌，它会给森林生态带来灾难性的后果。森林火灾在毁灭大片的森林的同时；还会烧伤、烧死大量的野生动物，降低森林更新能力；导致森林涵养水源的能力减弱，引发土壤的酸化和贫瘠，致使生态遭受破坏。
    1、森林火灾发生的过程中，大量的植物被烧毁，降低了森林中植被分布密度，破坏原有的森林植被结构；还引发植物类型的更替，一些低价值的灌木、杂草取代了以前经济生态价值较高的高大乔木，导致森林经济价值降低。
    2、由于植被遭到破坏，失去了保持水土、涵养水源的作用，大量土壤裸露，最终造成洪涝、干旱、山体滑坡、风沙扬尘等灾害的发生。
    3、因树木被林火烧伤，树木结构受到破坏，对外部的病虫害抵御能力降低，虫害肆虐，加快了树木死亡，使局域小气候受到干扰，需要漫长的时间才能恢复。
    4、森林火灾在烧毁大量经济林区和林业设施的同时，威胁到分布于林区附近的居民区，危及广大人民生命财产安全；同时森林火灾能烧死大量的野生动物，毁坏野生动物栖息地，降低野生动物种群数量；火灾发生时产生的大量粉尘及烟雾污染，会对周围大气环境造成巨大的影响；与此同时，扑救森林火灾要消耗大量的社会资源，同时影响工农业的正常生产活动，有时还会威胁人身安全，造成人员伤亡，影响社会的和谐稳定。

    出于降低森林火灾对人身财产安全以及保护生态的需求，本次设计通过分析往年森林火灾发生的因素，利用数据挖掘技术进行分析，为林业部门提供防控建议。

第二章 数据选取与方法

2.1数据来源

本次实验的数据来源源自于阿里云天池中的数据集，网址：https://tianchi.aliyun.com/dataset/dataDetail?dataId=92968，该数据集包含来自葡萄牙蒙特西尼奥自然公园的 517 起火灾，记录了每个事件的工作日、月份、坐标和烧伤区域，以及雨、温度、湿度和风等多个气象数据。通过读取数据并根据空间、时间和天气变量训练回归模型。

数据集注释：

X：编号。

Y：火灾发生年份。

Month：火灾发生月份。

Day：火灾所发生的工作日。

FFMC：细小可燃物浓度。

DMC：硫化物浓度。

DC： 空气污染物浓度。

ISI：空气质量指数。

Temp：火灾发生时的气温。

RH：火灾发生时的湿度。

Wind：风向。

Rain：火灾发生时的降雨量。

Area：过火面积。

2.2数据降维及预处理

数据集中共有12个维度，518条记录。数据记录由于是官方整理的数据，所以信息较为完整，无需进行补全操作，实验中只需根据需求进行切片分析即可。由于数据点较为密集，不容易直接观察特征，所以在K-means算法中选取其中前100条数据进行分析操作。

2.3机器学习算法

2.3.1线性回归算法

线性回归作为数据挖掘中最为简洁便利的算法，它的运行机制是运用线性回归方程中最小平方函数，对数据中一个或多个自变量和因变量之间存在的关系进行线性回归的一种模型分析方式，这种函数是一个或多个称为回归系数的模型参数的线性组合，数据集中只存在一个自变量的情况称为简单线性回归，存在多个自变量的情况被称为多元线性回归。如果变量中存在线性关系，那么就能直观的将线性关系展示出来。Sklearn是Python的一个包，也是机器学习中常用的一个模块，里面封装了很多机器学习的算法，不需要对机器学习算法的实现，只需要简单地调用Sklearn里相对应的模块中的LinearRegression方法即可。

算法的实际设计中首先选择引发森林火灾的因素中权重较大的两个进行拟合，通过分析数据集可以得到，数据集中的温度和湿度因素权重较大，所以在程序中以切片拆分的方式将temp（温度）、HR（湿度）两列单独拆分处理，并将数据传入变量a2、a3中，调用LinearRegression方法对数据进行拟合分析，最终得到数据的回归直线，该回归直线采用欧式距离进行划分，得到数据各点到该直线的最短距离，为后面结论分析提供支持。

2.3.2 K-means算法

K-means算法又称为k均值算法，K-means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。

其算法思想大致为：先从样本集中随机选取 k个样本作为簇中心，并计算所有样本与这 k个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。距离的计算采用欧氏距离作为标准，欧氏距离计算公式如下：

根据以上描述，我们大致可以猜测到实现K-means算法的主要四点：

（1）簇个数 k 的选择。

（2）各个样本点到“簇中心”的距离。

（3）根据新划分的簇，更新“簇中心”。

（4）重复上述2、3过程，直至"簇中心"没有移动。

实验设计过程中需要用到 Sklearn中的 K-Means算法，取数据集中前k个点作为初始中心，从样本中随机取k个点做初始聚类中心，设置随机数种子，待聚类样本目标聚成三类，在其中选取三个随机点；对每个样本，找到距离自己最近的中心点，完成一次聚类，判断此次聚类前后样本点的聚类情况是否相同，若相同，算法终止，否则继续下一步并根据本次聚类结果更新中心点；接下来循环进行判断直到与此次聚类前样本点的聚类情况是否相同，若相同，算法终止，同时返回迭代误差以及最终群集中心。最后通过Axes3D和Matplotlib两个库将数据以图像的方式输出出来。

第三章 结果与分析

3.1线性回归分析

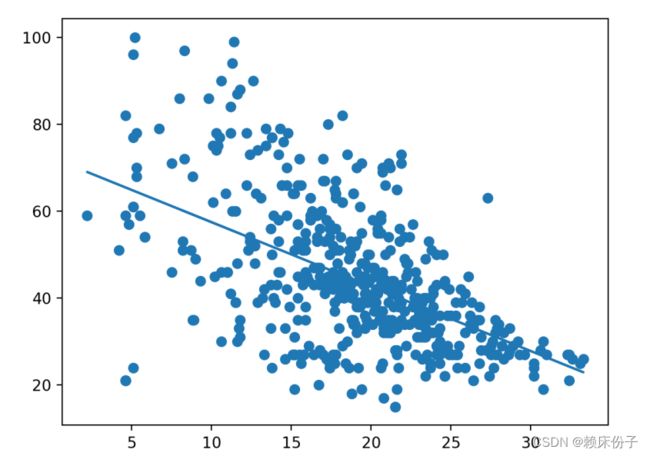
选取对于产生森林火灾中较为重要两条因素：温度和湿度条件进行线性回归分析，获得的结果如图2所示，在数据的散点图中存在一条直线将数据划分为两个部分，此直线表示了数据各点之间的最短欧氏距离，从图2中可以得到森林火灾发生时在何种温度和湿度下较为容易引发火灾，同时在现实的森林防火过程中将实际气温和湿度条件带入该图像，如果气温和湿度值达到或超过此直线将会有较大的火灾隐患。

线性回归分析

3.2聚类分析

在聚类分析中选定数据集中FFMC、DMC、DC、ISI、Temp列作为聚类分析的主要维度，由于数据量较大，故在聚类分析中只选取数据集中的前100行作为特征行。通过多次拟合分析，不断选取质心，提升模型的准确率，最终得到图3中所示图像，从第3次拟合开始数据聚类划分趋于稳定。在图4中，数据的变化反应了质心的迭代误差。

聚类划分

迭代误差

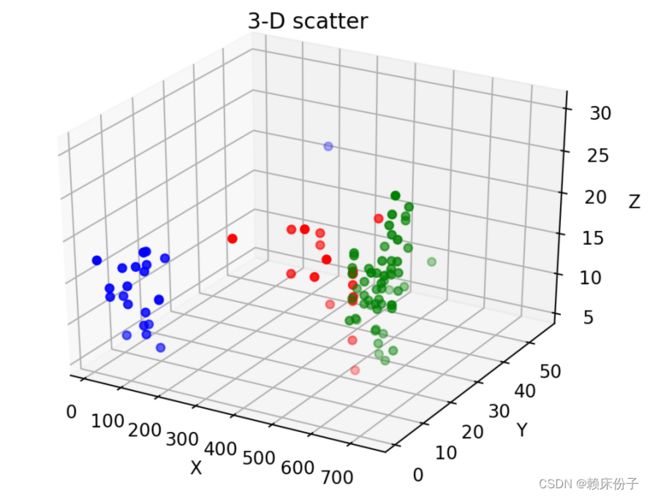
在经过初次数据的聚类划分后，可将质心以单独的方式显示出来，从图5中可以看到数据点围绕着质心分布，且各聚类之中的点分布较为集中，将图像三维化即可得到图6中所示的图像。

质心划分

三维散点图像

3.3火灾时间分布分析

首先通过读取数据集中的Month数据列，提取其中的数据进行整理并绘制出图像后，可以得到结果如图7所示。在图7中，可以直观的看到火灾发生较为频繁的时间为8-9月，其他月份相对较少；通过分析数据可得，由于葡萄牙位于北半球的欧洲地区，属海洋性气候与地中海气候的过渡地区，4-10月为旱季，8-9月气温较高，同时由于旱季还未结束，降水较少，空气中湿度降低，通过上文中线性回归分析的结果可知发生森林火灾的潜在风险较大；在8-9月的秋季，温带落叶阔叶林进入落叶期，大量的枯草落叶为森林火灾的发生提供了大量可燃物，加剧了森林火灾的发生。综合以上几点因素，8-9月为森林火灾的高发期，应加强管理力度。

 

历年火灾发生月份

第四章 结论

通过分析对于葡萄牙蒙特西尼奥自然公园森林火灾的数据可以得到，夏秋季节是火灾高发季节，干燥指数越高、温度越高，火灾发生的概率越大，过火面积越大。查阅资料发现，森林火灾的发生与高温、连续干旱、大风有密切关系，与分析得出来的结论大体相符，而葡萄牙为地中海气候，夏季炎热干燥，冬季低温湿润，与夏季为火灾高发季节相符。

在实验过程中得出以下森林火灾防控的建议：

1.提高人们防火意识
    多数森林火灾都是由于人为因素导致,因此要想进行森林防火工作必须先要提高人们的防火意识这是防火工作最为重要的一步。为提升人们的防火意识，各级政府应加强宣传力度，利用电视、报纸以及网络新媒体等方式宣传防火知识，让人们充分了解到森林火灾的巨大危害以及日常的防火措施。人们的防火意识提高了，在平时的工作、生活中就会有意识地进行防火，从而有效减少森林火灾的发生。

2.建立系统的森林火灾监控体系

随着科学技术的不断进步,各种新科技层出不穷,被各行业广为利用，为社会发展做出了突出贡献。而在森林防火领域中可以在森林中设置防火系统的方式提高监控效率，采用温控与烟控系统，通过调取气象数据，当森林温度、湿度、风力等条件达到算法临界值时，报警装置开始报警并通知相关部门进行处理,可以在森林火灾的发生之前进行处理，将损失最小化。

3.组建起一只高效的救火队伍
    一只拥有高水平、高效率的救火队伍是降低森林火灾造成损失的重要保证。救火队伍需定期组织巡逻，清除周边可能导致森林火灾发生的因素。救火队伍在接到森林火灾警报后,应第一时间到达火灾现场，并组织救援，防止火势进一步扩大，降低财产损失、降低人身安全威胁。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression

# https://tianchi.aliyun.com/dataset/dataDetail?dataId=92968  数据来源

# K-means 聚类分析
def InitCenter(k, m, x_train):
  Center = np.random.randn(k, n)
  Center = np.array(x_train.iloc[0 : k, :]) #取数据集中前k个点作为初始中心
  Center = np.zeros([k, n])         #从样本中随机取k个点做初始聚类中心
  np.random.seed(15)            #设置随机数种子
  for i in range(k):
    x = np.random.randint(m)
    Center[i] = np.array(x_train.iloc[x])
  return Center

def GetDistense(x_train, k, m, Center):
  Distence = []
  for j in range(k):
    for i in range(m):
      x = np.array(x_train.iloc[i, :])
      a = x.T - Center[j]
      Dist = np.sqrt(np.sum(np.square(a)))
      Distence.append(Dist)
  Dis_array = np.array(Distence).reshape(k, m)
  return Dis_array

def GetNewCenter(x_train, k, n, Dis_array):
  cen = []
  axisx, axisy, axisz = [], [], []
  cls = np.argmin(Dis_array, axis = 0)
  for i in range(k):
    train_i = x_train.loc[cls == i]
    xx, yy, zz = list(train_i.iloc[:, 1]), list(train_i.iloc[:, 2]), list(train_i.iloc[:, 3])
    axisx.append(xx)
    axisy.append(yy)
    axisz.append(zz)
    meanC = np.mean(train_i, axis = 0)
    cen.append(meanC)
  newcent = np.array(cen).reshape(k, n)
  NewCent = np.nan_to_num(newcent)
  return NewCent, axisx, axisy, axisz

def KMcluster(x_train, k, n, m, threshold):
  global axis_x, axis_y
  center = InitCenter(k, m, x_train)
  initcenter = center
  centerChanged = True
  t = 0
  while centerChanged:
    Dis_array = GetDistense(x_train, k, m, center)
    center, axis_x, axis_y, axis_z = GetNewCenter(x_train, k, n, Dis_array)
    err = np.linalg.norm(initcenter[-k:] - center)
    t += 1
    print('err of Iteration ' + str(t), 'is', err)
    plt.figure(1)
    p = plt.subplot(2, 3, t)
    p1, p2, p3 = plt.scatter(axis_x[0], axis_y[0], c = 'r'), plt.scatter(axis_x[1], axis_y[1], c = 'g'), plt.scatter(axis_x[2], axis_y[2], c = 'b')
    plt.legend(handles = [p1, p2, p3], labels = ['0', '1', '2'], loc = 'best')
    p.set_title('Iteration' + str(t))

    if err < threshold:
      centerChanged = False
    else:
      initcenter = np.concatenate((initcenter, center), axis = 0)
  plt.show()

  return center, axis_x, axis_y, axis_z, initcenter

if __name__=="__main__":

  x = pd.read_csv("C:/")
  x_train = x.iloc[1:100, 5:10]
  m, n = np.shape(x_train)
  k = 3
  threshold = 0.1
  km, ax, ay, az, ddd = KMcluster(x_train, k, n, m, threshold)
  print('Final cluster center is ', km)
  #2-Dplot
  plt.figure(2)
  plt.scatter(km[0, 1], km[0, 2], c = 'r', s = 550, marker = 'x')
  plt.scatter(km[1, 1], km[1, 2], c = 'g', s = 550, marker = 'x')
  plt.scatter(km[2, 1], km[2, 2], c = 'b', s = 550, marker = 'x')
  p1, p2, p3 = plt.scatter(axis_x[0], axis_y[0], c = 'r'), plt.scatter(axis_x[1], axis_y[1], c='g'), plt.scatter(axis_x[2], axis_y[2], c='b')
  plt.legend(handles = [p1, p2, p3], labels = ['0', '1', '2'], loc = 'best')
  plt.title('2-D scatter')
  plt.show()
  #3-Dplot
  plt.figure(3)
  TreeD = plt.subplot(111, projection = '3d')
  TreeD.scatter(ax[0], ay[0], az[0], c = 'r')
  TreeD.scatter(ax[1], ay[1], az[1], c = 'g')
  TreeD.scatter(ax[2], ay[2], az[2], c = 'b')
  TreeD.set_zlabel('Z') # 坐标轴
  TreeD.set_ylabel('Y')
  TreeD.set_xlabel('X')
  TreeD.set_title('3-D scatter')
  plt.show()


  # 线性回归模型
  a1 = LinearRegression()  # 调用模型
  a2 = x[["temp"]]
  a3 = x[["RH"]]
  a1.fit(a2, a3)  # 训练模型
  a4 = a1.predict(a2)  # 线性回归
  # 打印出图
  plt.scatter(a2, a3)
  plt.plot(a2, a4)
  plt.show()