【路径规划】局部路径规划算法——DWA算法（动态窗口法）|（含python实现）

参考资料

• The Dynamic Window Approach to Collision Avoidance
• 基于室内多障碍物复杂环境的路径规划方法研究
• 基于改进A*算法与改进DWA算法的无人驾驶汽车路径规划研究
• 室内移动机器人路径规划方法研究
• 机器人局部避障的动态窗口法

1. DWA算法原理

1.1 简介

• 动态窗口算法(Dynamic Window Approaches, DWA) 是基于预测控制理论的一种次优方法，因其在未知环境下能够安全、有效的避开障碍物, 同时具有计算量小, 反应迅速、可操作性强等特点。

• DWA算法属于局部路径规划算法。

• DWA算法的核心思想是根据移动机器人当前的位置状态和速度状态在速度空间 $(v,\omega )$ 中确定一个满足移动机器人硬件约束的采样速度空间，然后计算移动机器人在这些速度情况下移动一定时间内的轨迹， 并通过评价函数对该轨迹进行评价，最后选出评价最优的轨迹所对应的速度来作为移动机器人运动速度， 如此循环直至移动机器人到达目标点。

• 对于无人驾驶汽车而言，情况类似，将车辆的位置变化转化为线速度和角速度控制，避障问题转变成空间中的运动约束问题，这样可以通过运动约束条件选择局部最优的路径。

1.2 算法原理

• DWA算法的思路是：先通过机器人数学模型采集机器人速度样本，并预测模拟出在样本速度下一段时间内生成的运动轨迹， 并对这些运动轨迹进行标准评价， 选择出一组最优轨迹，机器人按照最优轨迹运动。机器人的运动姿态和方向是由机器人当前的线速度及角速度 (转向速度) 共同决定的。

• DWA算法主要包括3个步骤：速度采样、轨迹预测（推算）、轨迹评价。

1. 速度采样

由于移动机器人硬件、结构和环境等限制条件，移动机器人的速度采样空间 ${\mathbf{V}}_{\mathrm{s}}$ 中 $(v,\omega )$ 有一定的范围限制。该限制主要分为三大类：

• 速度边界限制

  根据移动机器人的硬件条件和环境限制, 移动机器人的速度存在的边界限制, 此时可采样的速度空间 ${\mathbf{V}}_m$ 为
  $${\mathbf{V}}_m=\left\{(v,\omega )\mid v\in \left[v_{\text{min }},v_{\text{max }}\right],\omega \in \left[{\omega }_{\text{min }},{\omega }_{\text{max }}\right]\right\}\text{\hspace{1em}(1)}$$
  式中 $v_{\text{min }}、v_{\text{max }}$ 分别为移动机器人最小线速度和最大线速度, ${\omega }_{\text{min }}、{\omega }_{\max }$ 分别 为移动机器人最小角速度和最大角速度。

• 加速度限制

  由于移动机器人的驱动电机的限制， 故移动机器人的线加速度和角加速度均存在边界限制，假设最大加速度和减速度大小一样，故考虑加速度时可采样的速度空间 ${\mathbf{V}}_d$ 为
  $${\mathbf{V}}_d=\left\{(v,\omega )\mid \begin{array}{l}v\in \left[v_c-a_{v\max }\cdot \Delta t,v_c+a_{v\max }\bullet \Delta t\right]\\ \omega \in \left[{\omega }_c-a_{w\max }\bullet \Delta t,{\omega }_c+a_{w\max }\bullet \Delta t\right]\end{array}\right\}\text{\hspace{1em}(2)}$$
  式中 $v_c、{\omega }_c$ 分别为移动机器人当前时刻的线速度和角速度，$a_{v\max }、a_{w\text{ max }}$ 分别为 移动机器人最大线加速度和最大角加速度。

• 环境障碍物限制

  局部规划还需要有动态实时的避障功能。考虑移动机器人的周围的障碍物因素，某一时刻移动机器人不与周围障碍物发生碰撞的可约束条件为
  $${\mathbf{V}}_a=\left\{(v,\omega )\mid \begin{array}{l}v\in \left[v_{\min },\sqrt{2\cdot dist(v,\omega )\cdot a_{v\max }}\right]\\ \omega \in \left[{\omega }_{\min },\sqrt{2\cdot dist(v,\omega )\cdot a_{\omega \max }}\right]\end{array}\right\}\text{\hspace{1em}(3)}$$

  式中$\mathrm{dist}(v,\omega )$表示当前速度下对应模拟轨迹与障碍物之间的最近距离。 在无障碍物的情况下 $\mathrm{dist}(v,\omega )$ 会是一个很大的常数值。当机器人运行采样速度在公式 (3) 范围时, 能够以最大减速度的约束实现安全减速直至避开障碍物。

  注意: 这个限制条件在采样初期是得不到的，需要我们先使用${\mathbf{V}}_m\cap {\mathbf{V}}_d$的速度组合采样模拟出轨迹后, 计算当前速度下对应模拟轨迹与障碍物之间的最近距离, 然后看当前采样的这对速度能否在碰到障碍物之前停下来， 如果能够停下来, 那这对速度就是可接收的。如果不能停下来, 这对速度就得抛弃掉。

  我在代码中并没有采用这种做法，而是直接计算机器人当前位置（并不是模拟轨迹）与障碍物的最近距离来得到${\mathbf{V}}_a$，算是一种比较投机的做法。

结合上述三类速度限制， 最终的移动机器人速度采样空间是三个速度空间的交集，即
$${\mathbf{V}}_s={\mathbf{V}}_m\cap {\mathbf{V}}_d\cap {\mathbf{V}}_a\text{\hspace{1em}(4)}$$

2. 轨迹预测（轨迹推算）

• 在确定速度采样空间 ${\mathbf{V}}_s$ 后，DWA算法以一定的采样间距（分辨率）在该空间均匀采样。

• 在速度空间中, 分别对线速度和角速度设置分辨率, 分别用 $E_w、E_v$ 表示采样分辨率，那么采样速度组的个数就可以确定下来, 如下式所示。
  $$n=\left[\left(v_{high}-v_{low}\right)/E_v\right]\cdot \left[\left(w_{high}-w_{low}\right)/E_w\right]$$
  式中的$v_{high},v_{low},w_{high},w_{low}$是速度空间的上下限。

  上式说明线速度每间隔一个 $E_v$ 大小取一个值, 角速度每间隔一个 $E_w$ 大小取一个值，由此组成了一系列的速度组。

• 当采样了一组 $(v,\omega )$ 后, 通过移动机器人（无人车辆）的运动学模型进行轨迹预测（即位置更新）。

• 因此，在轨迹预测阶段，只需要知道机器人（无人车辆）的运动学模型即可，然后在预测时间内保存预测轨迹便于后面处理。有关无人车的运动学模型可参考这篇博客。

• 这边不妨使用差分驱动移动机器人的运动学模型，那么轨迹预测就是计算下式：
  $$\begin{array}{rl}{x}_k& =x_{k-1}+v\cdot \cos ({\theta }_{k-1})\Delta t\\ y_k& =y_{k-1}+v\cdot \sin ({\theta }_{k-1})\Delta t\\ {\theta }_k& ={\theta }_{k-1}+\omega \Delta t\end{array}$$
  式中，$(x,y,\theta )$代表机器人的位姿，$k$代表采样时刻，$\Delta t$表示采样间隔。

上面轨迹推算这块是我比较肤浅的理解，因为按照原论文是需要假设相邻时间段内机器人的轨迹是圆弧，然后再进行轨迹推算，感兴趣的朋友可以直接查看原论文。

3. 轨迹评价

确定了机器人约束速度范围后，有一些速度模拟的轨迹是可行的， 但是还有不达标的轨迹， 这需要对采样得到的多组轨迹进行评价择优。通过标准评价轨迹， 比较评分来选出最优轨迹， 然后选取最优轨迹对应的速度作为驱动速度。对每条轨迹进行评估 的评价函数如公式 $(5)$ 所示。
$$G(v,\omega )=\sigma (\alpha \cdot \mathrm{heading}(v,\omega ))+\sigma (\beta \cdot \mathrm{dist}(v,\omega ))+\sigma (\gamma \cdot \mathrm{velocity}(v,\omega ))\text{\hspace{1em}(5)}$$

• heading $(v,\omega )$ 是方位角评价函数， 用作评估在当前采样速度下产生的轨迹终点位置方向与目标点连线的夹角的误差$\Delta \theta$；由于我们想要用评价函数越大表示越优，所以用$\pi -\Delta \theta$来参与评价，即$heading(v,\omega )=\pi -\Delta \theta$。

  

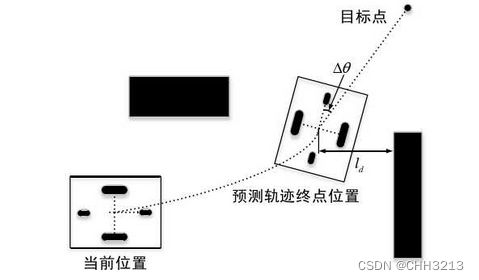
• $\mathrm{dist}(v,\omega )$ 是距离评价函数， 表示当前速度下对应模拟轨迹与障碍物之间的最近距离；如果没有障碍物或者最近距离大于设定的阈值，那么就将其值设为一个较大的常数值。

• velocity $(v,\omega )$ 是速度评价函数， 表示当前的速度大小，可以直接用当前线速度的大小来表示。它越大，表示规划轨迹上的速度越快，评价得分越高。

以上三种评价函数只是给了个大体的意思，并不绝对，例如有的人是把评价函数作为代价，代价越小，轨迹越优。可根据自己的想法进行评价函数的设置，但无论怎么变，这三种评价函数都是需要的。

$\alpha 、\beta$ 和 $\gamma$ 均为评价函数的系数。由于局部路径规划的过程需要多传感器的采集, 采集信息无法做到连续, 这样也会使得评价后差别较大, 所以可以进行归一化处理（平滑处理）， 其中 $\sigma$ 表示 归一化。

• 归一化处理过程如下式 (6) 所示:
  $$\begin{array}{rl}& \sigma \cdot \text{ heading }(v,\omega )=\text{normalize-heading}(i)=\frac{\mathrm{heading}(i)}{{\sum }_{i=1}^n\mathrm{heading}(i)}\\ & \sigma \cdot \mathrm{dist}(v,\omega )=\text{ normalize-dist }(i)=\frac{\mathrm{dist}(i)}{{\sum }_{i=1}^n\mathrm{dist}(i)}\\ & \sigma \cdot \mathrm{velocity}(v,\omega )=\text{ normalize-velocity }(i)=\frac{\text{ velocity }(i)}{{\sum }_{i=1}^n\text{ velocity }(i)}\end{array}\text{\hspace{1em}(6)}$$

  其中，$i$ 代表第$i$条模拟轨迹，$n$ 为约束条件下的全部采样轨迹总数。由上述公式 (5) 和公式 (6) 可以得出一条满足避开障碍物并朝着目标点快速行进的路径， 使得机器人完成局部路径最优规划。

DWA算法的流程如下图所示。

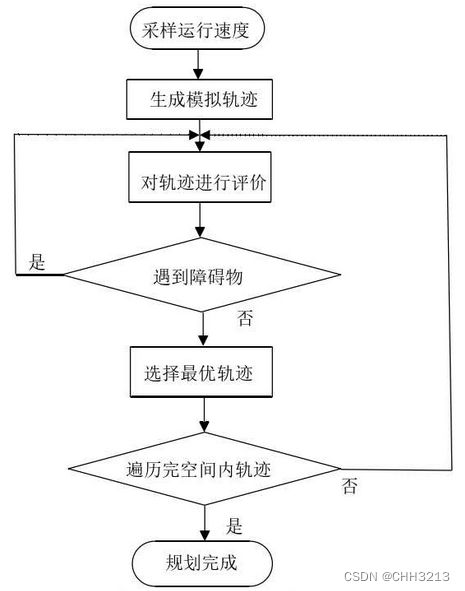
2. Python实现

完整程序请移步github仓库。
本次代码的参数配置和画图代码参考了AtsushiSakai/PythonRobotics 。

2.1 参数配置

使用一个类来保存需要设置的参数。

import numpy as np
import matplotlib.pyplot as plt
import copy
from celluloid import Camera  # 保存动图时用，pip install celluloid
import math

class Config:
    """
    simulation parameter class
    """

    def __init__(self):
        # robot parameter
        # 线速度边界
        self.v_max = 1.0  # [m/s]
        self.v_min = -0.5  # [m/s]
        # 角速度边界
        self.w_max = 40.0 * math.pi / 180.0  # [rad/s]
        self.w_min = -40.0 * math.pi / 180.0  # [rad/s]
        # 线加速度和角加速度最大值
        self.a_vmax = 0.2  # [m/ss]
        self.a_wmax = 40.0 * math.pi / 180.0  # [rad/ss]
        # 采样分辨率 
        self.v_sample = 0.01  # [m/s]
        self.w_sample = 0.1 * math.pi / 180.0  # [rad/s]
        # 离散时间间隔
        self.dt = 0.1  # [s] Time tick for motion prediction
        # 轨迹推算时间长度
        self.predict_time = 3.0  # [s]
        # 轨迹评价函数系数
        self.alpha = 0.15
        self.beta = 1.0
        self.gamma = 1.0

        # Also used to check if goal is reached in both types
        self.robot_radius = 1.0  # [m] for collision check
        
        self.judge_distance = 10 # 若与障碍物的最小距离大于阈值（例如这里设置的阈值为robot_radius+0.2）,则设为一个较大的常值

        # 障碍物位置 [x(m) y(m), ....]
        self.ob = np.array([[-1, -1],
                    [0, 2],
                    [4.0, 2.0],
                    [5.0, 4.0],
                    [5.0, 5.0],
                    [5.0, 6.0],
                    [5.0, 9.0],
                    [8.0, 9.0],
                    [7.0, 9.0],
                    [8.0, 10.0],
                    [9.0, 11.0],
                    [12.0, 13.0],
                    [12.0, 12.0],
                    [15.0, 15.0],
                    [13.0, 13.0]
                    ])
        # 目标点位置
        self.target = np.array([10,10])

值得注意的是，这边障碍物只给了位置，并没有给定大小，因为这边相当于把障碍物的大小合并到了机器人本体大小上，也即代码中的robot_radius上。

2.2 机器人运动学模型

主要用于轨迹推算。

def KinematicModel(state,control,dt):
  """机器人运动学模型

  Args:
      state (_type_): 状态量---x,y,yaw,v,w
      control (_type_): 控制量---v,w,线速度和角速度
      dt (_type_): 离散时间

  Returns:
      _type_: 下一步的状态
  """
  state[0] += control[0] * math.cos(state[2]) * dt
  state[1] += control[0] * math.sin(state[2]) * dt
  state[2] += control[1] * dt
  state[3] = control[0]
  state[4] = control[1]

  return state

在这里顺便保存了线速度和角速度作为状态分量，便于后面轨迹计算。

2.3 DWA算法类实现

通过一个类来实现DWA算法的速度采样、轨迹预测、轨迹评价三个主要步骤。

class DWA:
    def __init__(self,config) -> None:
        """初始化

        Args:
            config (_type_): 参数类
        """
        self.dt=config.dt
        self.v_min=config.v_min
        self.w_min=config.w_min
        self.v_max=config.v_max
        self.w_max=config.w_max
        self.predict_time = config.predict_time
        self.a_vmax = config.a_vmax
        self.a_wmax = config.a_wmax
        self.v_sample = config.v_sample # 线速度采样分辨率
        self.w_sample = config.w_sample # 角速度采样分辨率
        self.alpha = config.alpha
        self.beta = config.beta
        self.gamma = config.gamma
        self.radius = config.robot_radius
        self.judge_distance = config.judge_distance

    def dwa_control(self,state,goal,obstacle):
        """滚动窗口算法入口

        Args:
            state (_type_): 机器人当前状态--[x,y,yaw,v,w]
            goal (_type_): 目标点位置，[x,y]

            obstacle (_type_): 障碍物位置，dim:[num_ob,2]

        Returns:
            _type_: 控制量、轨迹（便于绘画）
        """
        control,trajectory = self.trajectory_evaluation(state,goal,obstacle)
        return control,trajectory


    def cal_dynamic_window_vel(self,v,w,state,obstacle):
        """速度采样,得到速度空间窗口

        Args:
            v (_type_): 当前时刻线速度
            w (_type_): 当前时刻角速度
            state (_type_): 当前机器人状态
            obstacle (_type_): 障碍物位置
        Returns:
            [v_low,v_high,w_low,w_high]: 最终采样后的速度空间
        """
        Vm = self.__cal_vel_limit()
        Vd = self.__cal_accel_limit(v,w)
        Va = self.__cal_obstacle_limit(state,obstacle)
        a = max([Vm[0],Vd[0],Va[0]])
        b = min([Vm[1],Vd[1],Va[1]])
        c = max([Vm[2], Vd[2],Va[2]])
        d = min([Vm[3], Vd[3],Va[3]])
        return [a,b,c,d]

    def __cal_vel_limit(self):
        """计算速度边界限制Vm

        Returns:
            _type_: 速度边界限制后的速度空间Vm
        """
        return [self.v_min,self.v_max,self.w_min,self.w_max]
    
    def __cal_accel_limit(self,v,w):
        """计算加速度限制Vd

        Args:
            v (_type_): 当前时刻线速度
            w (_type_): 当前时刻角速度
        Returns: 
            _type_:考虑加速度时的速度空间Vd
        """
        v_low = v-self.a_vmax*self.dt
        v_high = v+self.a_vmax*self.dt
        w_low = w-self.a_wmax*self.dt
        w_high = w+self.a_wmax*self.dt
        return [v_low, v_high,w_low, w_high]
    
    def __cal_obstacle_limit(self,state,obstacle):
        """环境障碍物限制Va

        Args:
            state (_type_): 当前机器人状态
            obstacle (_type_): 障碍物位置

        Returns:
            _type_: 某一时刻移动机器人不与周围障碍物发生碰撞的速度空间Va
        """
        v_low=self.v_min
        v_high = np.sqrt(2*self._dist(state,obstacle)*self.a_vmax)
        w_low =self.w_min
        w_high = np.sqrt(2*self._dist(state,obstacle)*self.a_wmax)
        return [v_low,v_high,w_low,w_high]

    def trajectory_predict(self,state_init, v,w):
        """轨迹推算

        Args:
            state_init (_type_): 当前状态---x,y,yaw,v,w
            v (_type_): 当前时刻线速度
            w (_type_): 当前时刻线速度

        Returns:
            _type_: _description_
        """
        state = np.array(state_init)
        trajectory = state
        time = 0
        # 在预测时间段内
        while time <= self.predict_time:
            x = KinematicModel(state, [v,w], self.dt) # 运动学模型
            trajectory = np.vstack((trajectory, x))
            time += self.dt

        return trajectory

    def trajectory_evaluation(self,state,goal,obstacle):
        """轨迹评价函数,评价越高，轨迹越优

        Args:
            state (_type_): 当前状态---x,y,yaw,v,w
            dynamic_window_vel (_type_): 采样的速度空间窗口---[v_low,v_high,w_low,w_high]
            goal (_type_): 目标点位置，[x,y]
            obstacle (_type_): 障碍物位置，dim:[num_ob,2]

        Returns:
            _type_: 最优控制量、最优轨迹
        """
        G_max = -float('inf') # 最优评价
        trajectory_opt = state # 最优轨迹
        control_opt = [0.,0.] # 最优控制
        dynamic_window_vel = self.cal_dynamic_window_vel(state[3], state[4],state,obstacle) # 第1步--计算速度空间
        
        # sum_heading,sum_dist,sum_vel = 0,0,0 # 统计全部采样轨迹的各个评价之和，便于评价的归一化
        # # 在本次实验中，不进行归一化也可实现该有的效果。
        # for v in np.arange(dynamic_window_vel[0],dynamic_window_vel[1],self.v_sample):
        #     for w in np.arange(dynamic_window_vel[2], dynamic_window_vel[3], self.w_sample):   
        #         trajectory = self.trajectory_predict(state, v, w)  

        #         heading_eval = self.alpha*self.__heading(trajectory,goal)
        #         dist_eval = self.beta*self.__dist(trajectory,obstacle)
        #         vel_eval = self.gamma*self.__velocity(trajectory)
        #         sum_vel+=vel_eval
        #         sum_dist+=dist_eval
        #         sum_heading +=heading_eval

        sum_heading,sum_dist,sum_vel = 1,1,1 # 不进行归一化
        # 在速度空间中按照预先设定的分辨率采样
        for v in np.arange(dynamic_window_vel[0],dynamic_window_vel[1],self.v_sample):
            for w in np.arange(dynamic_window_vel[2], dynamic_window_vel[3], self.w_sample):

                trajectory = self.trajectory_predict(state, v, w)  # 第2步--轨迹推算

                heading_eval = self.alpha*self.__heading(trajectory,goal)/sum_heading
                dist_eval = self.beta*self.__dist(trajectory,obstacle)/sum_dist
                vel_eval = self.gamma*self.__velocity(trajectory)/sum_vel
                G = heading_eval+dist_eval+vel_eval # 第3步--轨迹评价

                if G_max<=G:
                    G_max = G
                    trajectory_opt = trajectory
                    control_opt = [v,w]

        return control_opt, trajectory_opt

    def _dist(self,state,obstacle):
        """计算当前移动机器人距离障碍物最近的几何距离

        Args:
            state (_type_): 当前机器人状态
            obstacle (_type_): 障碍物位置

        Returns:
            _type_: 移动机器人距离障碍物最近的几何距离
        """
        ox = obstacle[:, 0]
        oy = obstacle[:, 1]
        dx = state[0,None] - ox[:, None]
        dy = state[1,None] - oy[:, None]
        r = np.hypot(dx, dy)
        return np.min(r)

    def __dist(self,trajectory,obstacle):
        """距离评价函数
        表示当前速度下对应模拟轨迹与障碍物之间的最近距离；
        如果没有障碍物或者最近距离大于设定的阈值，那么就将其值设为一个较大的常数值。
        Args:
            trajectory (_type_): 轨迹，dim:[n,5]
            
            obstacle (_type_): 障碍物位置，dim:[num_ob,2]

        Returns:
            _type_: _description_
        """
        ox = obstacle[:, 0]
        oy = obstacle[:, 1]
        dx = trajectory[:, 0] - ox[:, None]
        dy = trajectory[:, 1] - oy[:, None]
        r = np.hypot(dx, dy)
        return np.min(r) if np.array(r <self.radius+0.2).any() else self.judge_distance

    def __heading(self,trajectory, goal):
        """方位角评价函数
        评估在当前采样速度下产生的轨迹终点位置方向与目标点连线的夹角的误差

        Args:
            trajectory (_type_): 轨迹，dim:[n,5]
            goal (_type_): 目标点位置[x,y]

        Returns:
            _type_: 方位角评价数值
        """
        dx = goal[0] - trajectory[-1, 0]
        dy = goal[1] - trajectory[-1, 1]
        error_angle = math.atan2(dy, dx)
        cost_angle = error_angle - trajectory[-1, 2]
        cost = math.pi-abs(cost_angle)

        return cost

    def __velocity(self,trajectory):
        """速度评价函数， 表示当前的速度大小，可以用模拟轨迹末端位置的线速度的大小来表示

        Args:
            trajectory (_type_): 轨迹，dim:[n,5]

        Returns:
            _type_: 速度评价
        """
        return trajectory[-1,3]

从后面的实验效果上看，这边没有进行归一化也是可以的。

2.4 画图

主要用于机器人和方向箭头的绘制。

def plot_arrow(x, y, yaw, length=0.5, width=0.1):  # pragma: no cover
    plt.arrow(x, y, length * math.cos(yaw), length * math.sin(yaw),
              head_length=width, head_width=width)
    plt.plot(x, y)


def plot_robot(x, y, yaw, config):  # pragma: no cover
        circle = plt.Circle((x, y), config.robot_radius, color="b")
        plt.gcf().gca().add_artist(circle)
        out_x, out_y = (np.array([x, y]) +
                        np.array([np.cos(yaw), np.sin(yaw)]) * config.robot_radius)
        plt.plot([x, out_x], [y, out_y], "-k")

2.5 主函数

def main(config):
    # initial state [x(m), y(m), yaw(rad), v(m/s), omega(rad/s)]
    x = np.array([0.0, 0.0, math.pi / 8.0, 0.0, 0.0])
    # goal position [x(m), y(m)]
    goal = config.target

    # input [forward speed, yaw_rate]

    trajectory = np.array(x)
    ob = config.ob
    dwa = DWA(config)
    fig=plt.figure(1)
    camera = Camera(fig)
    while True:
        u, predicted_trajectory = dwa.dwa_control(x,goal, ob)

        x = KinematicModel(x, u, config.dt)  # simulate robot
        trajectory = np.vstack((trajectory, x))  # store state history
        plt.cla()
        # for stopping simulation with the esc key.
        plt.gcf().canvas.mpl_connect(
            'key_release_event',
            lambda event: [exit(0) if event.key == 'escape' else None])
        plt.plot(predicted_trajectory[:, 0], predicted_trajectory[:, 1], "-g")
        plt.plot(x[0], x[1], "xr")
        plt.plot(goal[0], goal[1], "xb")
        plt.plot(ob[:, 0], ob[:, 1], "ok")
        plot_robot(x[0], x[1], x[2], config)
        plot_arrow(x[0], x[1], x[2])
        plt.axis("equal")
        plt.grid(True)
        plt.pause(0.001)

        # check reaching goal
        dist_to_goal = math.hypot(x[0] - goal[0], x[1] - goal[1])
        if dist_to_goal <= config.robot_radius:
            print("Goal!!")
            break
        # camera.snap()
        # print(x)
        # print(u)

    print("Done")
    plt.plot(trajectory[:, 0], trajectory[:, 1], "-r")
    plt.pause(0.001)
    # camera.snap()
    # animation = camera.animate()
    # animation.save('trajectory.gif')
    plt.show()


main(Config())

运行主函数，即可得到下图所示的效果：

3. 总结

起初在不了解之前我以为DWA算法是一种很难实现的算法，但最近因为毕设想要用到这个传统方法进行对比，所以花了点时间去看别人写的论文，发现DWA算法的原理比较简单，代码实现也比较简单，并没有我想象中得那么困难。所以还是不能有畏难心理！

在实际调试过程中发现评价函数的设置非常重要，设置的不好，以及参数设置的不好（例如评价函数的系数），那么就极有可能算法失效。也看了一些别人写的论文，针对DWA算法的改进基本也是集中在评价函数上，所以如果需要改进效果的话不妨从这上面入手。