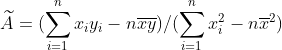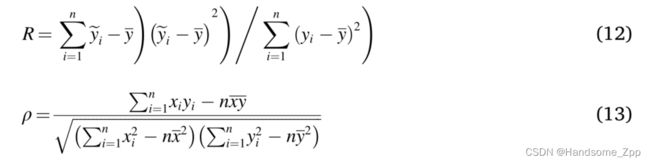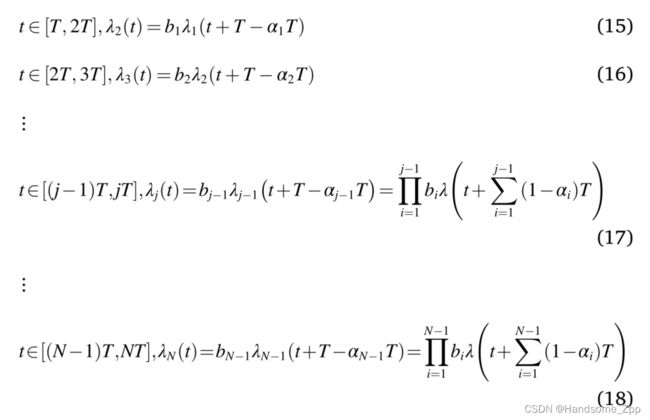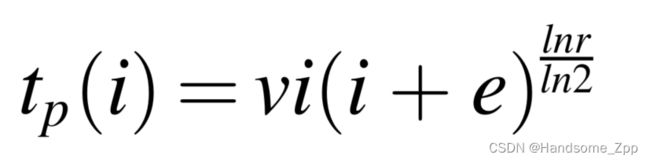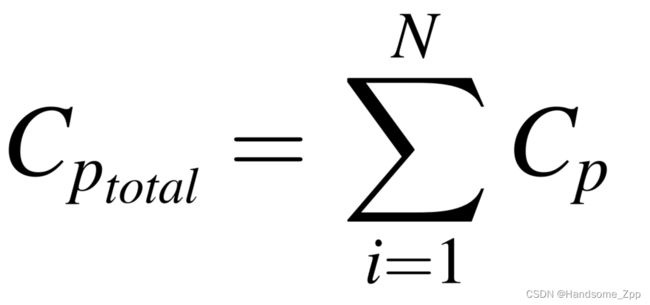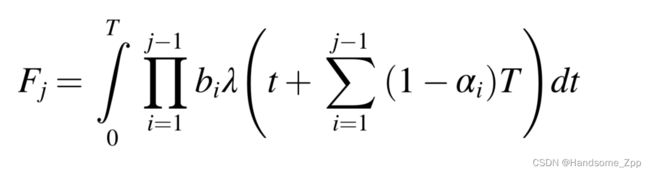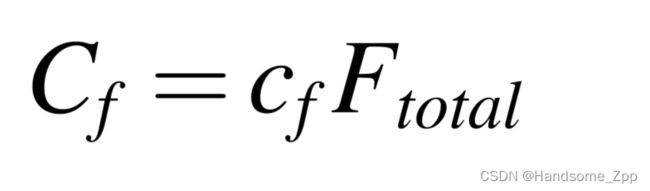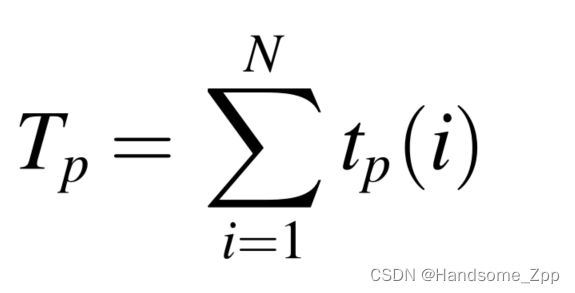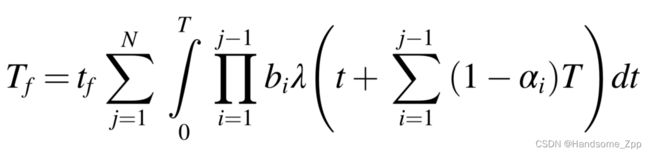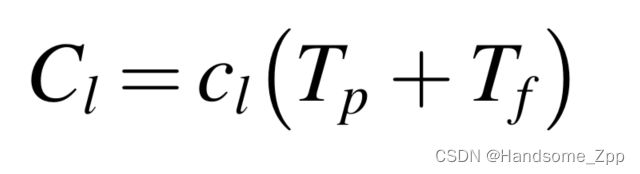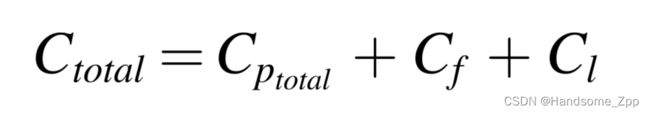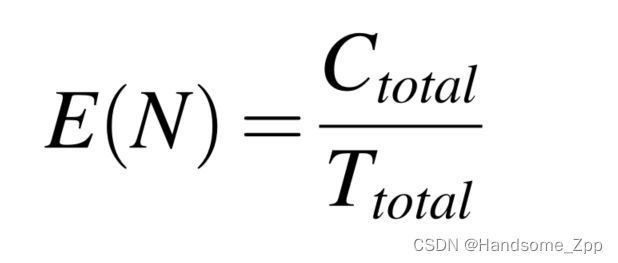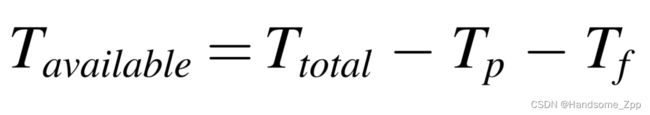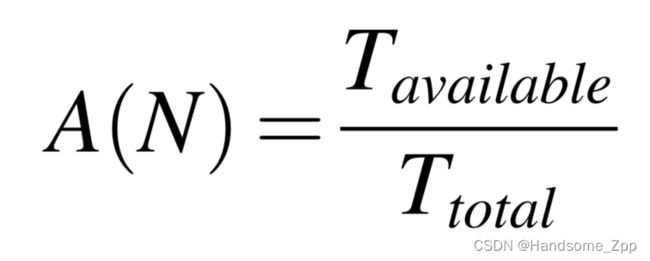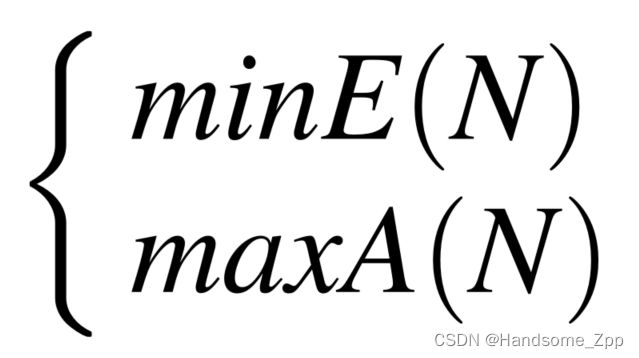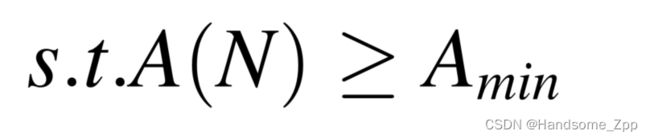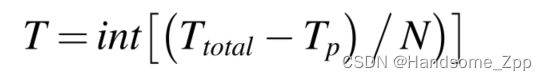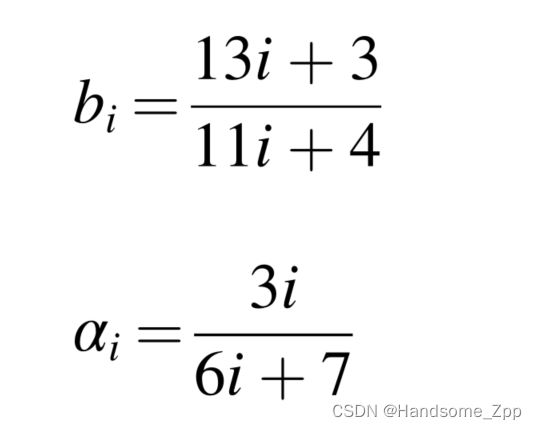基于多目标优化方法的电梯零部件预防性维修期决策
电梯维护对电梯的安全可靠运行起着至关重要的作用。然而，目前电梯维修是在一些相关的规范和标准下进行的，对如何对电梯零部件进行维修期决策的研究较少。此外，电梯维护周期的不合理选择会造成成本过高，设备运行效率低下。提出了一种电梯零部件维修决策方法，旨在解决电梯零部件合理维修周期的确定问题。首先，利用电梯零部件的历史故障数据分析其故障分布规律。为了准确反映零件在维修后的变化，引入了寿命降低因子和故障率增加因子，建立了混合故障率模型。在此基础上，综合考虑维修过程中的成本和时间因素，建立了成本率和使用率模型。建立了以检修频率为决策变量的多目标优化模型。然后，利用蒙特卡罗模拟方法对优化模型进行求解，得到了零件在使用时间内的最佳维修周期。最后，将该方法应用于电梯零部件的最优维修频率，结果表明该方法是有效的。合理的维修周期不仅可以降低设备故障风险，还可以节约成本，避免资源的过度浪费。
1引言：
电梯是一种由多个部件组成的复杂机电一体化设备[1，2]。电梯的安全可靠运行有赖于电梯内部各部件的正常运行。由于电梯长期运行，内部部件出现故障在所难免。即使单个部件出现异常，也会对整个电梯系统的安全产生影响。预防性维护通过提前对设备进行维修和维护，从而在问题发生之前预防问题，从而降低设备故障的风险。合理的维修决策不仅可以减少设备的故障频率，还可以减少资源的浪费，提高设备的运行效率。
随着维修技术的快速发展，\“事中事后维修\”的维修理念已不能满足复杂可修设备的要求。国内外学者对机电设备的预防性维修做了大量的研究。Barlow等人。[4]提出了零件最小维修策略，这是一种维修后策略。Malik等人。[5]提出了减龄因子模型。减龄现象主要体现了赡养的实际效果。Nakagawa等人。[6]提出了故障率增加因子模型。Chareonsuk等人。[7]提出了一种以总预期成本为目标函数的多准则方法来计算造纸厂生产线部件的最优预防性维修间隔。Allaoui等人。[8]针对有约束的混流车间设备计划维修问题，提出了一种集成仿真优化方法。Wu等人。[9]用威布尔分布建立了断路器部件的故障率分布，并利用平均成本率优化模型得到各部件的检修周期。文献[10-16]描述了机械系统的维修建模和优化。Duan et al.。[17]利用估计的故障时间分布构造费用函数，以长期期望成本率最小为优化目标计算预防性维修周期。
不完全维修模型是研究预防性维修的常用方法。不完全维修是指设备的部件或子系统在一次维修后会有所改进，但不会像新的一样进行维修。不完全维修模型的研究内容如下。Lin等人。[18]建立了基于减龄因子模型的不完全维修模型，该模型适用于可修复和不可修复两种失效模式。文献[19，20]对不完善的维修模型和维修策略进行了研究，旨在降低设备部件的故障率和维修成本。以生产预期利润最大为优化目标，Gouiaa等人提出。[21]通过融合制造系统维护不完善和维护不完善两种情况，提出了一种新的、改进的不完善预防性维护策略。Khatab等人。[22]采用不完全维修模型，以总期望成本率最低为优化目标，计算出设备零部件在有限使用时间内的最佳维修周期。基于不完善的维修模型，沈等人提出了一种新的维修模式。[23]以设备利用率为目标函数，计算设备的维修周期。Yu等人。[24]提出了一种序贯不完全预防性维修模型，并利用该模型降低了城市公交车的故障概率。Yue et al.。[25]利用不完全维修模型，以检修过程中的费用最低为优化目标，建立了复杂周期巡检系统的最优维修策略。
本文提出的方法是对上述研究的补充，旨在解决维修周期不合理的问题。在电梯维修领域。本文的第一个贡献是建立了基于元器件历史故障数据的元器件故障分布规律模型，并对元器件故障分布进行了分析。对零件的维护和维修会产生一定的影响。为了更好地反映维修过程的实际情况，本文引入了寿命折减因子和故障率递增因子。基于故障率函数和年龄降低因子和故障率增加因子建立了混合故障率模型。上述研究大多只把成本作为单一的目标函数。本文在前人研究的基础上，综合考虑维修过程中的各种成本因素和时间因素，建立了成本率函数和使用率函数。建立了以最小成本率和最大利用率为目标的多目标优化模型。
这项工作的其余部分安排如下。第二节对电梯零部件故障分布模型进行了分析，并对其参数进行了估计。第三节建立了电梯零部件维修期的多目标优化模型。第四节给出了多目标优化模型的求解方法，第五节讨论了求解结果。最后，第六节对本文的主要工作进行了总结。
2电梯零部件故障分布模型
2.1理论分布模型
Weibull 分布技术是用于精确故障分析和故障预测以及老化和可靠性的最广泛使用的技术之一[26]。这是一个非常灵活的分布模型，可以用来描述浴缸曲线所有三个阶段的失效分布。本文采用威布尔分布来描述电梯零部件的失效分布。威布尔（Weibull ）分布的分布函数、概率密度函数和失效率函数如下。
分布函数：
![F(t)=1-exp[-(\frac{t}{\eta })^{\beta }]](http://img.e-com-net.com/image/info8/d8ecbde7a6074d75aac6f2a89e861aa8.gif){kind=small}
(1)
概率密度函数：
![f(t)=\frac{\beta }{\eta }(\frac{t}{\eta })^{\beta -1}exp[-(\frac{t}{\eta })^{\beta }]](http://img.e-com-net.com/image/info8/1a4d95d1359b4a6d9d6bf9744966a536.gif){kind=small}
(2)
故障率函数：
(3)
t表示样本数据的时间统计，η称为尺度参数，β称为形状参数。形状参数β是Weibull 分布的关键特征，使其能够应用于浴缸曲线的任何阶段。
2.2参数估计方法
最小二乘法 [9] 用于拟合 Weibull 分布中的参数。 Weibull分布中未知参数的最小二乘法估计过程如下。
1）Weibull 参数可以由方程式中给出的回归线公式（4）确定：
yi = Axi + B （4）
其中A代表回归线的斜率，B代表回归线的截距，i代表样本数据从小到大的顺序。
2）方程式（4）中 A 和 B 的值。 根据历史样本数据计算得出，
和 
分别代表A和B的估计值，回归线的斜率A和截距B计算如下:
(5)
(6)
3）方程式(4) 中的 xi 和 yi。计算如下：
(7)
(8)
其中 ti 是等级 i 中失效组件的独立时间。
4) 故障事件 i 的中间等级F(ti)由公式计算:
(9)
5) 威布尔分布的形状参数可以用方程来计算:
(10)
6) 刻度参数可以用公式来计算:
![\eta =exp[-(\frac{\widetilde{B}}{\widetilde{A}})]](http://img.e-com-net.com/image/info8/65d732bd315043eeb57a5bbca8895b65.gif){kind=small}
(11)
7) 检验数据之间的拟合优度和线性相关性。线性相关系数的拟合优度检验公式由下式给出：
其中，R代表拟合度，R越接近1，拟合效果越好；ρ是拟合数据之间的线性相关性，ρ越接近1，数据之间的线性相关性越高。
3电梯零部件的预防性维修模式
3.1电梯零部件的混合故障率模型
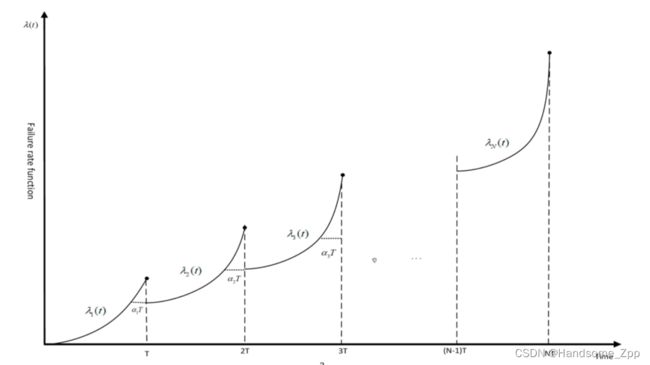
为了使已建立的理论模型更接近实际情况，本文引入了年龄降低因子[5]αi和故障率增加因子[6]bi。年龄的降低代表了维护的实际效果。每一次定期检修后，部件故障率都会回到检修前某一时刻对应的水平。然而，在一次维修后，故障率不会降为零，这是\“修复为新的\”。但维修后故障率会发生变化，不会出现以旧换新的现象。维修后，零件的故障率介于\“新修\”和\“旧修\”之间，即“不完善维修”。故障率的增加表明部件在一次维修后故障率加快的现象。维修过程中零件的拆卸、修理、安装可能会使一些零件的性能变差，部件的潜在故障隐患可能是维修过程中操作不当或技术不熟练造成的。将年龄降低因子和故障率增加因子相结合，形成了混合故障率模型。有限使用时间内零件的混合故障率模型[19]如图1所示。
图1 电梯部件混合故障率模型示意图
根据图1中故障率函数的变化，表明每次检修后，零件的寿命都会准时恢复到检修前的“(1−αi)T”水平，故障率上升得更快。以下是部件在每个维护周期内故障率函数表达式的递归关系。当部件在第一个维修周期内投入使用时，t∈[0，T]，λ1(T)=λ(T)。当第一次维修的时间 T 出现时，第一次维修后出现减龄，故障率函数变化较快。在第二个维护周期中，t∈[T，2T]，λ2(T)=b1λ1(t+T−α1T)。类似地，在第三个维修周期∈[2T，3T]，λ3(T)=b2λ2(t+T−α2T)等期间，每个维修周期的故障率函数的表达式如下：
T∈[0，T]，λ1(T)=λ(T) （14）
其中，1≤i≤N，部件在有限的使用时间内进行N次预防性维护。在上述公式中，αi是年龄降低因子，bi是故障率增加因子，αi和bi不是常量，它们符合特定的形式。
3.2多目标优化模型
本文从预防性维护成本Cp、故障后修复成本 Cf 和维护维修过程造成的停机成本 Cl 三个方面考虑了电梯零部件维护的成本因素。
3.2.1预防性维护成本
预防性维护成本分为两部分：人工成本Cv和材料成本Cs：Cp=Cv+Cs (19)
人工成本与预防性维护的时间呈线性关系：Cv = ltp，其中 tp 表示预防性维护的时间，l 表示人工成本系数。
预防性维护的时间 tp 是维护次数的函数，表示为：
其中，v代表预防性维护的调整系数，e代表经验参数，代表维护人员的经验程度，r代表经验曲线的百分比。
预防性维护总成本表示为：
3.2.2 维修后成本
每次故障后的平均维修成本为 cf。根据图1所示的部件故障率的变化规律，部件在[(j−1)T，jT]维修周期内的故障次数可表示为：
部件在整个维修周期内的总故障次数可表示如下：
事后的总维修费用可表示为：
3.2.3 损失的停机成本
停机时间包括预防性维护时间和故障后维修时间。预防性维修时间为tp，每次故障后的平均维修时间为tf，单位时间内的停机损失为cl 。
预防性维护的总时间如下：
故障后维修的总时间为：
停机损失的总成本写成：
总成本可以表示为：
总成本率由(30)表示：
使用率[23]是指部件的可用性，它表示部件的有效工作时间与整个有限使用时间的比率，反映了设备的运行效率。
电梯部件不能工作的时间可以分为两段。第一个是预防性维护所花费的时间，第二个是进行事后维修的时间。零件的有效工作时间可表示为：
使用率如下：
在电梯零部件的有限使用时间内，以最低成本率[22]和最大利用率为目标，建立了电梯零部件维修周期的多目标优化模型：
以维修次数N为决策变量，应满足以下约束条件：(其中，Amin代表最低利用率。)
T(total)代表零件的有限使用时间，成本率和利用率以维修次数N为自变量，维修周期T与维修次数N之间的关系可近似表示为：
4解决方案
用蒙特卡罗模拟方法[27]计算了电梯部件的最优维修期。蒙特卡罗模拟求解多目标优化模型的核心是不断调整最大维修频次的取值，以限制模拟次数，得到维修频次、利用率和成本率之间的关系。以最低成本率和最大利用率来确定零件的最佳维修频率和最佳维修周期。蒙特卡罗模拟的具体过程如表1所示。
5数值计算实例
5.1参数估计与讨论
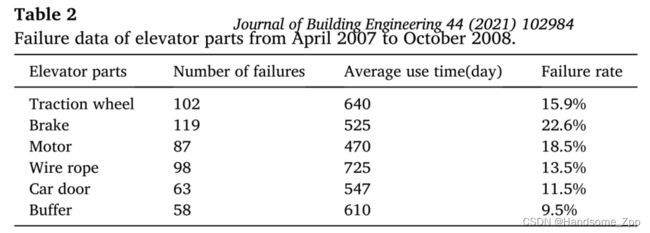
对沈阳市特种设备检测研究院提供的2007年4月至2008年10月电梯零部件故障记录数据进行了分析。具体部件的故障统计数据如表2所示。
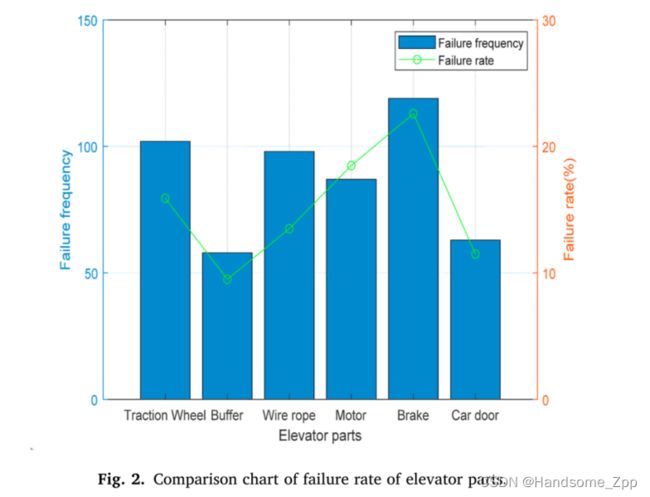
从零件的历史统计来看，制动器的故障频率最高，达到22.6%。缓冲器的故障频率保持在相对较低的水平。其余部件的失效频率有一定差异，但故障率基本在相同范围内。各部件的故障频率如图2所示。
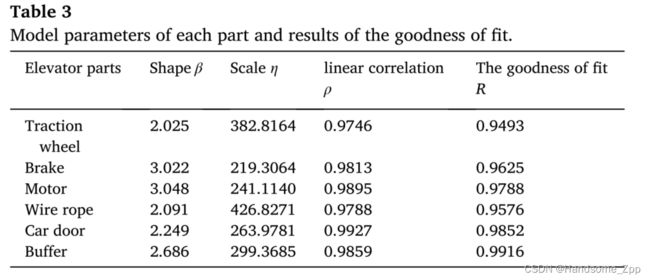
利用威布尔分布技术对零件失效数据进行分析的过程包括数据整理、数据提取和结果解释。各部分的参数估计结果如表3所示。
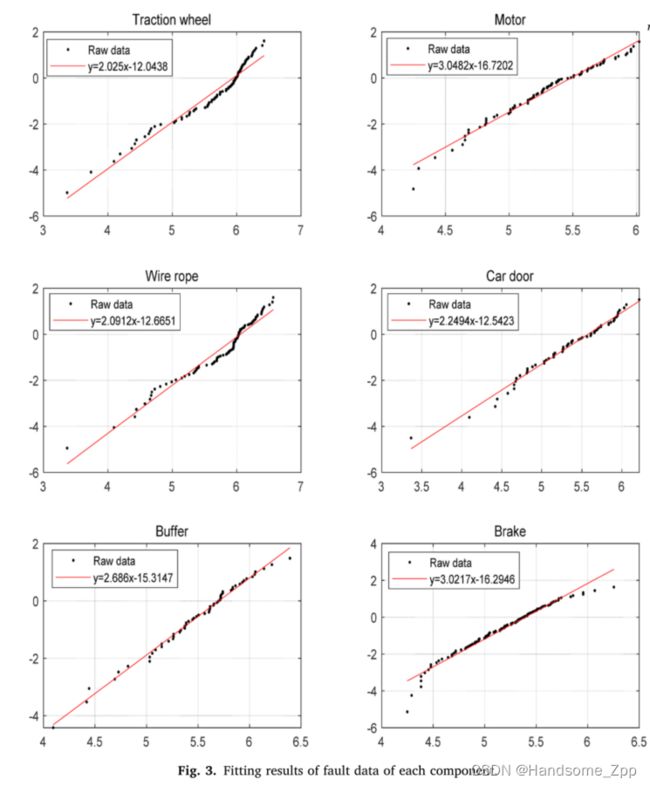
对各子部件的故障数据进行处理后，按照第2.2节所述的方法，得到各部件的威布尔分布参数。通过估计后的试验结果可以看出，各部件在其服役时间内的故障分布服从威布尔分布。元件故障数据的拟合结果如图3所示。
采用最小二乘法对零件的故障数据进行拟合，得到故障分布函数中的参数估计。通过拟合结果可以看出，故障数据分布在回归线附近。通过公式计算回归直线的截距和斜率。(5)和等式。(6)。相应地，根据方程求出了零件威布尔分布函数的形状参数和尺度参数。(10)和公式。(11)。最后，用公式验证了拟合结果的准确性。(12)和公式。(13)。根据表3所示的计算结果，拟合精度满足要求。
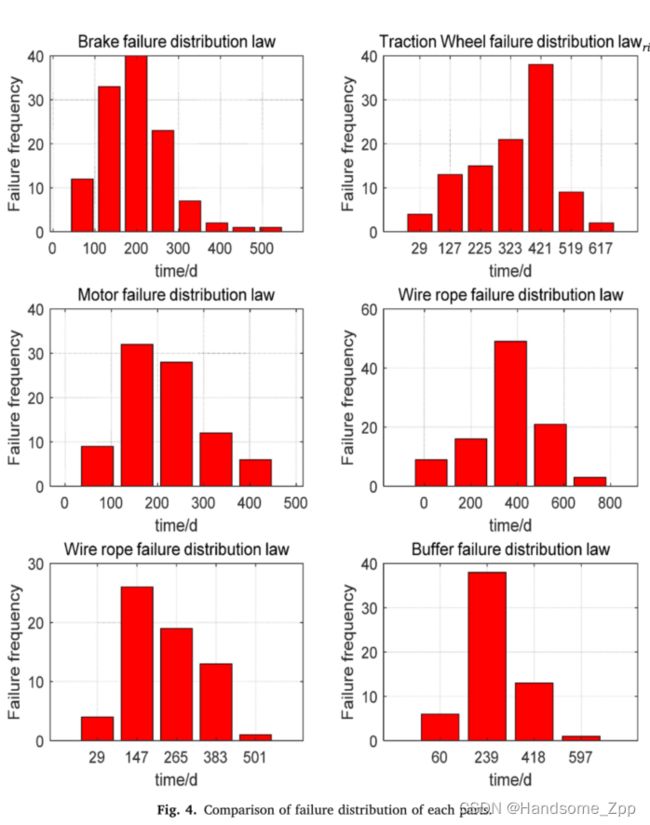
每个部件的故障分布时间如图4所示。由于电梯中不同部件的位置和功能不同，其故障发生的时间段也不同。在使用了100多天后，电梯的刹车和电机出现故障的频率更高。钢丝绳和牵引轮在使用约400天后发生故障的频率较高。电梯门和缓冲器的故障频发集中在100天至200天。
5.2优化模型仿真
选取上述六种成分作为分析对象。将故障分布规律模型与不完全维修模型相结合，建立了电梯零部件维修周期的多目标优化模型。相关参数取值如下。
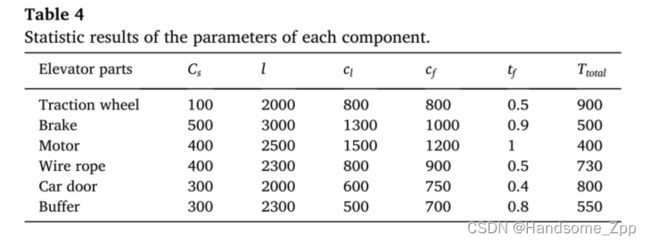
六个分量的相同参数设置为：V=0.3e=4r=0.85，Amin=0.3。各部件的形状参数β和比例参数η的计算结果如表3所示。经过大量的数据采集和统计，得出了各部件剩余参数的计算结果。统计结果如表4所示。参考文献[22]，故障率增加因子bi和年龄降低因子αi的形式如下：
其中i表示维护的数量。
将上述数据分别放入成本率模型和利用率模型中。用蒙特卡罗模拟方法进行计算，得到检修频次与成本率、利用率的关系图。
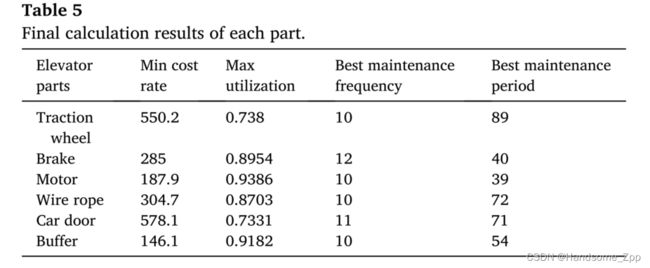
根据上述方法计算出各部件的成本率和利用率。本文以制动器为分析对象，分析了制动器维护过程中的成本变化和时间变化。最后，表5显示了每个部件的最低成本率、最大利用率和合适的维护周期。
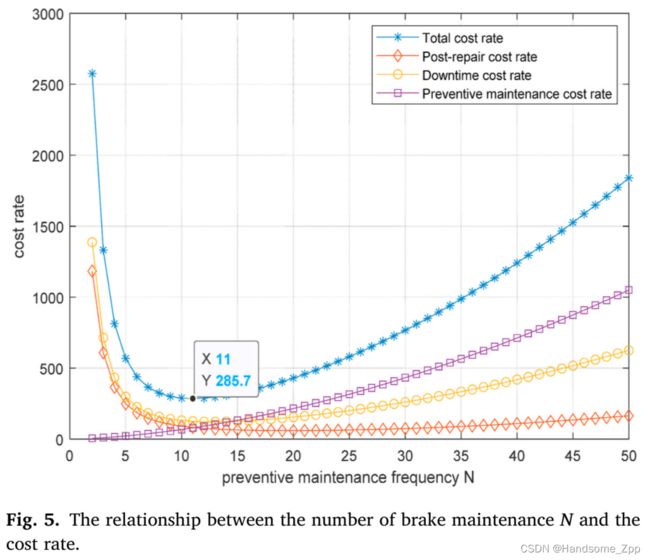
总成本率、预防性维护成本率、修后成本率、停机损失成本率与制动器维护频率的关系如图5所示，当维护频率为11次左右时，总成本率最低。分析其原因，可能是因为当检修次数少于11次时，制动故障较多，且维修后成本较高。而且由于维修造成的停机时间会很长，停机损失的成本也会比较高。当维修次数大于11次时，随着维修次数的增加，维修时间变长，预防性维修成本增加。随着维护造成的停机时间增加，停机损失成本增加，总成本增加。
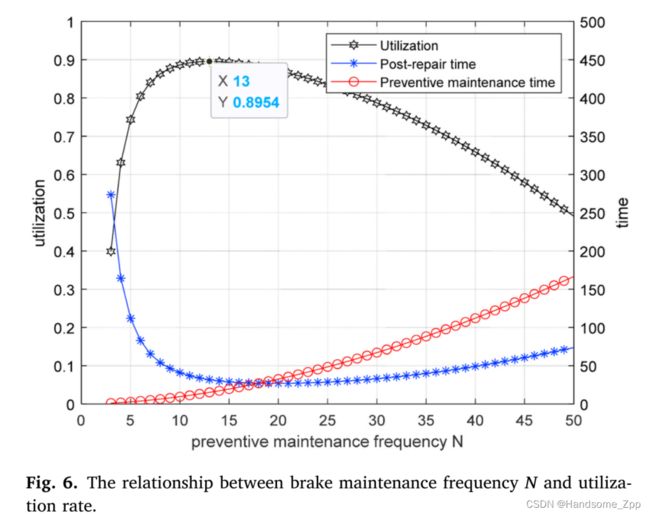
使用率、修后时间、预防性维护时间与制动器维护次数的关系如图6所示，当维护次数为13次时，制动器的使用率达到最大。当维护频次低于13次时，由于维护次数较少，制动故障频率较高，维护后时间较长，利用率较低。当检修频次超过13次时，随着检修次数的增加，检修时间会增加，零件的利用率会逐渐降低。
综合以上两部分的仿真结果，从图5可以看出，N=11，成本率E(N)最小，为285.7。此时，对应的维修期为44天。还表明，当N=13时，利用率A(N)达到最大值，为0.8954，此时维护周期为37天。为达到上述两个目标，制动器每40天可检修一次，共检修12次。
根据表2和图4的结果，根据统计数据，与其他五个部件相比，制动失效率最高。电梯制动器在使用100天内故障频率较低，使用100天以上故障维修频率逐渐增加。根据本文的计算结果，平均每40天检修一次，可以最大程度地节约检修成本，减少制动器的故障频率。
根据表5中的结果对电梯零部件进行维护，可以最大限度地提高使用效率，最大限度地降低维护成本。本文计算的结果不仅可以有效地减少资源浪费，提高设备的运行效率，而且还可以降低电梯零部件故障的风险，起到防患于未然的作用。
6结论
基于电梯零部件的历史故障数据，利用最小二乘法对威布尔分布模型中的未知参数进行估计，分析了电梯零部件在不同阶段的失效概率分布。本文建立的混合故障率模型能够清晰地表达零件在每个维修周期内故障率的变化。将维修过程中的成本因素分为预防性维修成本、维修后成本和停机损失成本三部分进行考虑。然后结合混合失效率模型建立了成本率函数。充分考虑了维修过程中的时间因素，建立了利用函数。如果维修周期短，设备和零部件故障的风险就会降低，但频繁的维修会增加成本，降低设备运行效率。另一方面，如果维修周期长，设备和零部件故障的风险就会增加。以最小成本率和最大利用率为目标函数，以零件在使用寿命内的维修次数为决策变量，建立了多目标优化模型。最后通过蒙特卡罗仿真得到了优化模型的解和最佳检修频率。通过实际运行测试，证明本文提出的方法可以解决电梯维护周期不合理的问题，为电梯维护团队提供进一步的帮助。
该方法致力于解决电梯零部件的维修期决策问题。在建模过程中考虑了各种成本和时间因素，以获得合理的维修周期，使电梯零部件维修过程中的成本最小，利用率最高。这项研究有望对降低设备故障风险、避免过度浪费资源起到一定的作用。获得的维护周期可以提供给建筑物所有者和设施管理团队，以便在他们的级别改进故障分析。
今后，将开展基于电梯实时运行数据的电梯性能评价研究。根据电梯评估结果及其健康状况分析，将形成新的维护策略。将相应的新策略与本文提出的策略相结合，得到针对实际电梯维护的组合维护决策。