Kmeans聚类分析

该算法可以将数据划分为指定的k个簇，并且簇的中心点由各簇样本均值计算所得
该聚类算法的思路非常通俗易懂，就是不断地计算各样本点与簇中心之间的距离，直到收敛为止，其具体的步骤如下：
（1）从数据中随机挑选k个样本点作为原始的簇中心。
（2）计算剩余样本与簇中心的距离，并把各样本标记为离k个簇中心最近的类别。
（3）重新计算各簇中样本点的均值，并以均值作为新的k个簇中心。
（4）不断重复（2）和（3），直到簇中心的变化趋于稳定，形成最终的k个簇。

KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, 
	precompute_distances='auto', verbose=0, random_state=None, 
	copy_x=True, n_jobs=1, algorithm='auto')
	
n_clusters：用于指定聚类的簇数。

init：用于指定初始的簇中心设置方法，如果为'k-means++'，则表示设置的初始簇中心之间相距较远；如果为'random'，则表示从数据集中随机挑选k个样本作为初始簇中心；如果为数组，则表示用户指定具体的簇中心。

n_init：用于指定Kmeans算法运行的次数，每次运行时都会选择不同的初始簇中心，目的是防止算法收敛于局部最优，默认为10。

max_iter：用于指定单次运行的迭代次数，默认为300。

tol：用于指定算法收敛的阈值，默认为0.0001。

precompute_distances：bool类型的参数，是否在算法运行之前计算样本之间的距离，默认为'auto'，表示当样本量与变量个数的乘积大于1200万时不计算样本间距离。

verbose：通过该参数设置算法返回日志信息的频度，默认为0，表示不输出日志信息；如果为1，就表示每隔一段时间返回一次日志信息。

random_state：用于指定随机数生成器的种子。

copy_x：bool类型参数，当参数precompute_distances为True时有效，如果该参数为True，就表示提前计算距离时不改变原始数据，否则会修改原始数据。

n_jobs：用于指定算法运算时使用的CPU数量，默认为1，如果为-1，就表示使用所有可用的CPU。

algorithm：用于指定Kmeans的实现算法，可以选择'auto' 'full'和'elkan'，默认为'auto'，表示自动根据数据特征选择运算的算法。

最佳k值的确定

拐点法

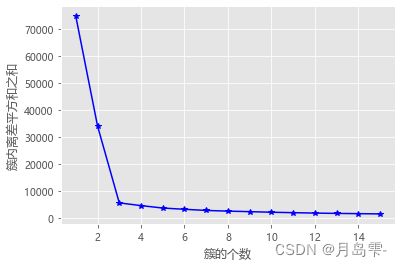
就是在不同的k值下计算簇内离差平方和，然后通过可视化的方法找到“拐点”所对应的k值。正如前文所介绍的Kmeans聚类算法的目标函数J，随着簇数量的增加，簇中的样本量会越来越少，进而导致目标函数J的值也会越来越小。通过可视化方法，重点关注的是斜率的变化，当斜率由大突然变小时，并且之后的斜率变化缓慢，则认为突然变化的点就是寻找的目标点，因为继续随着簇数k的增加，聚类效果不再有大的变化。
为了验证这个方法的直观性，这里随机生成三组二元正态分布数据，首先基于该数据绘制散点图

# 导入第三方包
import pandas as pd
import numpy as np  
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics

# 随机生成三组二元正态分布随机数 
np.random.seed(1234)
mean1 = [0.5, 0.5]
cov1 = [[0.3, 0], [0, 0.3]]
x1, y1 = np.random.multivariate_normal(mean1, cov1, 1000).T

mean2 = [0, 8]
cov2 = [[1.5, 0], [0, 1]]
x2, y2 = np.random.multivariate_normal(mean2, cov2, 1000).T

mean3 = [8, 4]
cov3 = [[1.5, 0], [0, 1]]
x3, y3 = np.random.multivariate_normal(mean3, cov3, 1000).T

# 绘制三组数据的散点图
plt.scatter(x1,y1)
plt.scatter(x2,y2)
plt.scatter(x3,y3)
# 显示图形
plt.show()

# 构造自定义函数，用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
    # 选择连续的K种不同的值
    K = range(1,clusters+1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
        # 计算总的簇内离差平方和 
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与GSSE的关系
    plt.plot(K, TSSE, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('簇内离差平方和之和')
    # 显示图形
    plt.show()

# 将三组数据集汇总到数据框中
X = pd.DataFrame(np.concatenate([np.array([x1,y1]),np.array([x2,y2]),np.array([x3,y3])], axis = 1).T)
# 自定义函数的调用
k_SSE(X, 15)

轮廓系数法

。有关轮廓系数的计算，可以直接调用sklearn子模块metrics中的函数，即
silhouette_score。需要注意的是，该函数接受的聚类簇数必须大于等于2。下面基于该函数重新自定义一个函数，用于绘制不同k值下对应轮廓系数的折线图

# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')    
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()
    
# 自定义函数的调用
k_silhouette(X, 15)

当k等于3时，轮廓系数最大，且比较接近于1，说明应该把虚拟数据聚为3类比较合理

间隔统计量法

# 自定义函数，计算簇内任意两样本之间的欧氏距离
def short_pair_wise_D(each_cluster):
    mu = each_cluster.mean(axis = 0)
    Dk = sum(sum((each_cluster - mu)**2)) * 2.0 * each_cluster.shape[0]
    return Dk

# 计算簇内的Wk值
def compute_Wk(data, classfication_result):
    Wk = 0
    label_set = set(classfication_result)
    for label in label_set:
        each_cluster = data[classfication_result == label, :]
        Wk = Wk + short_pair_wise_D(each_cluster)/(2.0*each_cluster.shape[0])
    return Wk

# 计算GAP统计量 
def gap_statistic(X, B=10, K=range(1,11), N_init = 10):
    # 将输入数据集转换为数组
    X = np.array(X)
    # 生成B组参照数据
    shape = X.shape
    tops = X.max(axis=0)
    bots = X.min(axis=0)
    dists = np.matrix(np.diag(tops-bots))
    rands = np.random.random_sample(size=(B,shape[0],shape[1]))
    for i in range(B):
        rands[i,:,:] = rands[i,:,:]*dists+bots
    
    # 自定义0元素的数组，用于存储gaps、Wks和Wkbs
    gaps = np.zeros(len(K))
    Wks = np.zeros(len(K))
    Wkbs = np.zeros((len(K),B))
    # 循环不同的k值，
    for idxk, k in enumerate(K):
        k_means =  KMeans(n_clusters=k)
        k_means.fit(X)
        classfication_result = k_means.labels_
        # 将所有簇内的Wk存储起来
        Wks[idxk] = compute_Wk(X,classfication_result)
        
        # 通过循环，计算每一个参照数据集下的各簇Wk值
        for i in range(B):
            Xb = rands[i,:,:]
            k_means.fit(Xb)
            classfication_result_b = k_means.labels_
            Wkbs[idxk,i] = compute_Wk(Xb,classfication_result_b)

    # 计算gaps、sd_ks、sk和gapDiff
    gaps = (np.log(Wkbs)).mean(axis = 1) - np.log(Wks)        
    sd_ks = np.std(np.log(Wkbs), axis=1)
    sk = sd_ks*np.sqrt(1+1.0/B)
    # 用于判别最佳k的标准，当gapDiff首次为正时，对应的k即为目标值
    gapDiff = gaps[:-1] - gaps[1:] + sk[1:]
    
    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制gapDiff的条形图
    plt.bar(np.arange(len(gapDiff))+1, gapDiff, color = 'steelblue')
    plt.xlabel('簇的个数')
    plt.ylabel('k的选择标准')
    plt.show()
    
# 自定义函数的调用
gap_statistic(X)    

x轴代表了不同的簇数k，y轴代表k值选择的判断指标gapDiff，gapDiff首次
出现正值时对应的k为3。所以，对于虚拟的数据集来说，将其划分为3个簇是比较合理的，同样与预设的簇数一致。代码中自定义了3个函数，分别用于计算公式中的Dk、Wk和Gapk，虽然计算逻辑比较简单，但是涉及的循环比较多，所以对大数据集而言，其k值的确定会比较慢。

Kmeans聚类的应用

在做Kmeans聚类时需要注意两点，一个是聚类前必须指定具体的簇数k值，如果k值是已知的，可以直接调用cluster子模块中的Kmeans类，对数据集进行分割；如果k值是未知的，可以根据行业经验或前面介绍的三种方法确定合理的k值；另一个是对原始数据集做必要的标准化处理，由于Kmeans的思想是基于点之间的距离实现“物以聚类”的，所以，如果原始数据集存在
量纲上的差异，就必须对其进行标准化的预处理，否则可以不用标准化。数据集的标准化处理可以借助于sklearn子模块preprocessing中的scale函数或minmax_scale实现

iris数据集的聚类

iris数据集经常被用于数据挖掘的项目案例中，它反映了3种鸢尾花在花萼长度、宽度和花瓣长度、宽度之间的差异，一共包含150个观测，且每个花种含有50个样本。下面将利用数据集中的四个数值型变量，对该数据集进行聚类，且假设已知需要聚为3类的情况下

# 读取iris数据集
iris = pd.read_csv(r'iris.csv')
# 查看数据集的前几行
iris.head()

	Sepal_Length	Sepal_Width	Petal_Length	Petal_Width	Species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

# 提取出用于建模的数据集X
X = iris.drop(labels = 'Species', axis = 1)
# 构建Kmeans模型
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 聚类结果标签
X['cluster'] = kmeans.labels_
# 各类频数统计
X.cluster.value_counts()

0    62
1    50
2    38
Name: cluster, dtype: int64

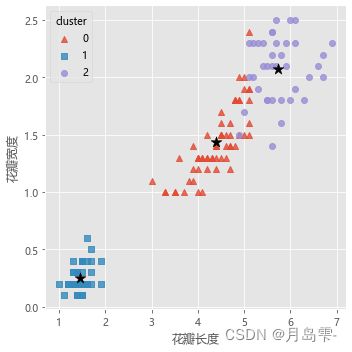
如上结果所示，通过设定参数n_clusters为3就可以非常方便地得到三个簇，并且各簇样本量分别为62、50和38。为了直观验证聚类效果，不妨绘制花瓣长度与宽度的散点图，对比原始数据的三类和建模后的三类差异

# 导入第三方模块
import seaborn as sns

# 三个簇的簇中心
centers = kmeans.cluster_centers_
# 绘制聚类效果的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'cluster', markers = ['^','s','o'], 
           data = X, fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.scatter(centers[:,2], centers[:,3], marker = '*', color = 'black', s = 130)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()

# 增加一个辅助列，将不同的花种映射到0,1,2三种值，目的方便后面图形的对比
iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,'versicolor':2})
# 绘制原始数据三个类别的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'Species_map', data = iris, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()

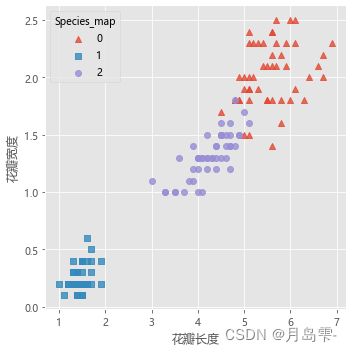
，左图为聚类效果的散点图，其中五角星为每个簇的簇中心；右图为原始分
类的散点图。从图中可知，聚类算法将标记为1的所有花种聚为一簇，与原始数据吻合；对于标记为0和2的花种，聚类算法存在一些错误分割，但绝大多数样本的聚类效果还是与原始数据比较一致的。为了直观对比三个簇内样本之间的差异，使用雷达图对四个维度的信息进行展现，绘图所使用的数据为簇中心。雷达图的绘制需要导入pygal模块，需要读者提前在Python中安装该模型，绘图代码如下

# 导入第三方模块
import pygal
# 调用Radar这个类，并设置雷达图的填充，及数据范围
radar_chart = pygal.Radar(fill = True)
# 添加雷达图各顶点的名称
radar_chart.x_labels = ['花萼长度','花萼宽度','花瓣长度','花瓣宽度']

# 绘制三个雷达图区域，代表三个簇中心的指标值
radar_chart.add('C1', centers[0])
radar_chart.add('C2', centers[1])
radar_chart.add('C3', centers[2])
# 保存图像
radar_chart.render_to_file('radar_chart.svg')

NBA球员数据集的聚类

NBA球员数据集却是未知分类个数的，对于这样的数据集就需要通过探索方法获知理想的簇数k值，然后进行聚类操作。该数据集来自于虎扑体育网，一共包含286名球员的历史投篮记录，这些记录包括球员姓名、所属球队、得分、各命中率等信息

# 读取球员数据
players = pd.read_csv(r'players.csv')
players.head()


排名	球员	球队	得分	命中-出手	命中率	命中-三分	三分命中率	命中-罚球	罚球命中率	场次	上场时间
0	1	詹姆斯-哈登	火箭	31.9	9.60-21.10	0.454	4.20-10.70	0.397	8.50-9.90	0.861	30	36.1
1	2	扬尼斯-阿德托昆博	雄鹿	29.7	10.90-19.90	0.545	0.50-1.70	0.271	7.50-9.80	0.773	28	38.0
2	3	勒布朗-詹姆斯	骑士	28.2	10.80-18.80	0.572	2.10-5.10	0.411	4.50-5.80	0.775	32	37.3
3	4	斯蒂芬-库里	勇士	26.3	8.30-17.60	0.473	3.60-9.50	0.381	6.00-6.50	0.933	23	32.6
4	4	凯文-杜兰特	勇士	26.3	9.70-19.00	0.510	2.50-6.30	0.396	4.50-5.10	0.879	26	34.8

从数据集来看，得分、命中率、三分命中率、罚球命中率、场次和上场时间都为数值型变量，并且量纲也不一致，故需要对数据集做标准化处理。这里不妨挑选得分、命中率、三分命中率和罚球命中率4个维度用于球员聚类的依据。首先绘制球员得分与命中率之间的散点图，便于后文比对聚类后的效果

# 绘制得分与命中率的散点图
sns.lmplot(x = '得分', y = '命中率', data = players, 
           fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'})
plt.show()

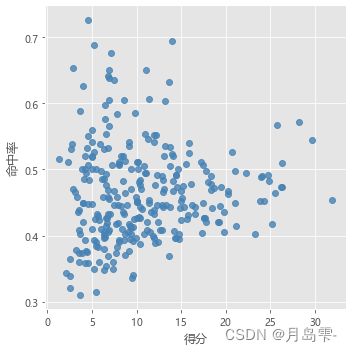
通过肉眼，似乎无法直接对这286名球员进行分割。如果需要将这些球员
聚类的话，该划为几类比较合适呢？下面将利用前文介绍的三种选择k值的方法，对该数据集进行测试，代码如下：

from sklearn import preprocessing
# 数据标准化处理
X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])
# 将数组转换为数据框
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
# 使用拐点法选择最佳的K值
k_SSE(X, 15)

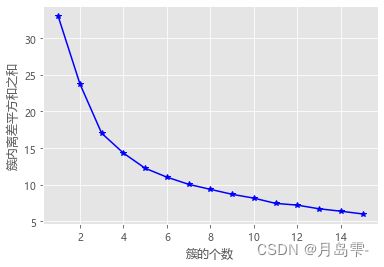
随着簇数k的增加，簇内离差平方和的总和在不断减小，当k在4附近时，折线斜率的变动就不是很大了，故可选的k值可以是3、4或5。为了进一步确定合理的k值，再参考轮廓系数和间隙统计量的结果

# 使用轮廓系数选择最佳的K值
k_silhouette(X, 15)
# 使用间隙统计量选择最佳的K值
gap_statistic(X, B = 20, K=range(1, 16))

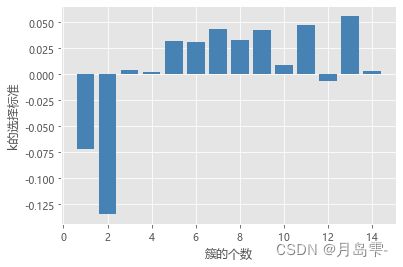
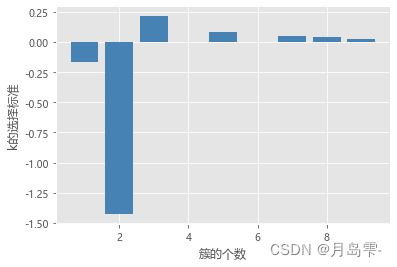
左图为轮廓系数图，右图为Gap Statistic图。对于左图而言，当k值为2时对
应的轮廓系数最大；在右图中，纵坐标首次为正时所对应的k值为3。故综合考虑上面的三种探索方法，将最佳的聚类个数k确定为3。接下来基于这个k值，对NBA球员数据集进行聚类，然后基于分组好的数据，重新绘制球员得分与命中率之间的散点图

# 将球员数据集聚为3类
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 将聚类结果标签插入到数据集players中
players['cluster'] = kmeans.labels_
# 构建空列表，用于存储三个簇的簇中心
centers = []
for i in players.cluster.unique():
    centers.append(players.loc[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean())
# 将列表转换为数组，便于后面的索引取数
centers = np.array(centers)

# 绘制散点图
sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False)
# 添加簇中心
plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180)
plt.xlabel('得分')
plt.ylabel('命中率')
# 图形显示
plt.show()

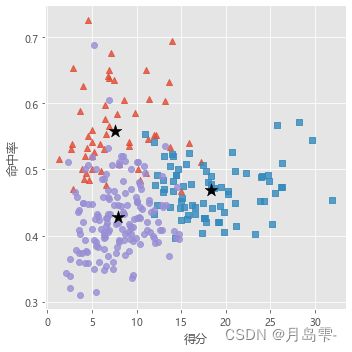
三类散点图看上去很有规律，其中五角星代表各个簇的中心点。对比正
方形和圆形的点，它们之间的差异主要体现在命中率上，正方形所代表的球员属于低得分低命中率型，命中率普遍在50%以下；圆形所代表的球员属于低得分高命中率型。再对比正方形和三角形的点，它们的差异体现在得分上，三角形所代表的球员属于高得分低命中率型，当然，从图中也能发现几个强悍的球员，即高得分高命中率（如图5-12中圈出的三个点）。需要注意的是，由于对原始数据做了标准化处理，因此图中的簇中心不能够直接使用
cluster_centers_方法获得，因为它返回的是原始数据标准化后的中心。故在代码中通过for循环重新找出了原始数据下的簇中心，并将其以五角星的标记添加到散点图中。最后看看三类球员的雷达图，比对四个指标上的差异。由于四个维度间存在量纲上的不一致，故需要使用标准化后的中心点绘制雷达图

# 雷达图
# 调用模型计算出来的簇中心
centers_std = kmeans.cluster_centers_
# 设置填充型雷达图
radar_chart = pygal.Radar(fill = True)
# 添加雷达图各顶点的名称
radar_chart.x_labels = ['得分','罚球命中率','命中率','三分命中率']

# 绘制雷达图代表三个簇中心的指标值
radar_chart.add('C1', centers_std[0])
radar_chart.add('C2', centers_std[1])
radar_chart.add('C3', centers_std[2])
# 保存图像
radar_chart.render_to_file('radar_chart.svg')