策略梯度法（policy gradient）算法简述

本文通过整理李宏毅老师的机器学习教程的内容，简要介绍深度强化学习（deep reinforcement learning）中的策略梯度法（policy gradient）。

李宏毅老师课程的B站链接：
李宏毅, 深度强化学习, policy gradient

相关笔记：
近端策略优化（proximal policy optimization）算法简述
DQN（deep Q-network）算法简述
actor-critic 相关算法简述

设：
一次游戏的轨迹（trajectory）：$\tau$
玩家（actor）策略（policy）：$\theta$

则激励（reward）的期望值可通过 N 次采样（sampling）估算（激励 $R$ 是一个随机变量）：
$${\bar{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )\approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)$$

最优策略为：
$${\theta }^{\ast }=\arg \underset{\theta }{\max }{\bar{R}}_{\theta }$$

优化方法即为梯度上升法（gradient ascent）。
激励的梯度：
$$▽{\bar{R}}_{\theta }=\sum _{\tau }R(\tau )▽P(\tau |\theta )=\sum _{\tau }R(\tau )P(\tau |\theta )\frac{▽P(\tau |\theta )}{P(\tau |\theta )}=\sum _{\tau }R(\tau )P(\tau |\theta )▽\ln P(\tau |\theta )\approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)▽\ln P({\tau }^n|\theta )$$

其中，取对数的操作原理：
$$\frac{d\ln (f(x))}{dx}=\frac{1}{f(x)}\frac{df(x)}{dx}$$

由于轨迹在策略的条件发生的概率：
$$P(\tau |\theta )=p(s_1)p(a_1|s_1,\theta )p(r_1,s_2|s_1,a_1)p(a_2|s_2,\theta )p(r_2,s_3|s_2,a_2)\cdots =p(s_1)\prod _{t=1}^{T}p(a_t|s_t,\theta )p(r_t,s_{t+1}|s_t,a_t)$$

其中，$s$ 为各时刻的游戏状态（state），$a$ 为玩家的动作（action）。
只有 $p(a_t|s_t,\theta )$ 部分与玩家的策略 $\theta$ 有关，另外两项 $p(s_1)$ 和 $p(r_t,s_{t+1}|s_t,a_t)$ 均与玩家策略无关。

因此对数项的梯度：
$$\begin{gathered} \ln P(\tau |\theta )=\ln p(s_1)+\sum _{t=1}^T[\ln p(a_t|s_t,\theta )+\ln p(r_t,s_{t+1}|s_t,a_t)] \\ ▽\ln P(\tau |\theta )=\sum _{t=1}^T▽\ln p(a_t|s_t,\theta ) \end{gathered}$$

从而得出激励的梯度：
$$▽{\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)▽\ln P({\tau }^n|\theta )=\frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)\sum _{t=1}^{T_n}▽\ln p(a_t^n|s_t^n,\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n)▽\ln p(a_t^n|s_t^n,\theta )$$

需要注意以下几点：

一，上式所乘的激励为全局收益，而非单步激励，否则无法学习到对后续时刻激励的动作。（第四点会做出相应改进）

二，取对数的原因：

由于取对数再求梯度相当于，对概率求梯度后除以概率本身：
$$▽\ln p(a_t^n|s_t^n,\theta )=\frac{▽p(a_t^n|s_t^n,\theta )}{p(a_t^n|s_t^n,\theta )}$$

而除以概率本身，可以防止某些激励不高的动作被采样多次，从而导致累积过多激励的结果：

三，引入基线（baseline）：

当游戏的激励恒非负时，为防止未被采样到的高激励动作的概率值降低，故加入基线：

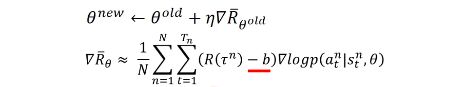
基线的一个最简单的设置方式，即对 $R(\tau )$ 取平均值：
$$b\approx E[R(\tau )]$$

四，给每个动作分配合适的分数（credit）：

每个时刻的动作，只考虑该时间点之后直到游戏结束的所有激励的总和：
$$▽{\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(\sum _{t^{\prime }=t}^{T_n}{r}_{t^{\prime }}^n-b)▽\ln p(a_t^n|s_t^n,\theta )$$

进一步地，把未来的激励做一个折扣（discount），即时间越久，影响力就越小：
$$▽{\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b)▽\ln p(a_t^n|s_t^n,\theta )$$

其中，折扣因子 $\gamma$ 取值范围为 $[0,1]$，通常取 $0.9$ 或 $0.99$，若取 $0$，则表示只关心即时激励，若取 $1$，则表示未来激励等同于即时激励。