(深度学习社区发现综述)A Comprehensive Survey on Community Detection with Deep Learning

论文地址
推荐直接看原文。
译文

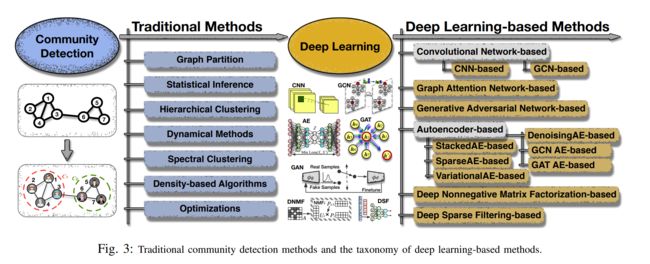
深度学习分类框架，包括基于深度神经网络、深度非负矩阵分解和深度稀疏滤波的深度学习模型，并进一步将深度神经网络模型细分为卷积网络，图注意网络，生成对抗网络和自编码器。

对于一些小型的网络和简单的场景，研究人员已经提出了一系列基于谱聚类、统计推断等传统技术的社区发现方法。然而，由于计算及存储空间成本巨大，这类方法并没有扩展到大型网络或具有高维特征的网络上。在现实世界的网络中，大量的非线性结构信息使传统的模型并不能够很好地应用于实际场景。因此，我们需要发展出具有良好计算性能的更强大的技术。如今，针对这一问题，深度学习从以下3个方面给出了最为灵活的解决方案：（1）学习非线性网络属性，如节点之间的关系；（2）提供能够保留复杂网络结构特征的低维网络表示；（3）利用更多信息进行社区发现以提高性能。

符号与定义：

如果节点$V$有属性$X=\{x_i{\}}_1^n$ ，$G=(V,E,X)$ 为属性网络，其中$X_i\subseteq R^d$ 表示节点 $v_i$的属性向量，否则 $G$为无属性网络。当网络随时间 $t$演化时，即为动态网络 $G(t)=(V_t,E_t)$或时态网络 $G(t)=(V,E,X_t)$。

• 社区发现输入： 基于深度学习的社区发现模型将网络结构和其它属性信息作为输入，如节点属性和带符号的边。网络结构是以节点和边代表的拓扑关系。边上的权重代表连接强度。节点属性代表节点的语义信息，例如在线社交网络中用户的账号信息。带符号的边代表连接状态，如正连接（+）和负连接（-）。
• 社区发现输出： 社区发现模型的输出通常是一些将节点和边分组后的社区，这些社区可以是重叠或非重叠的。。

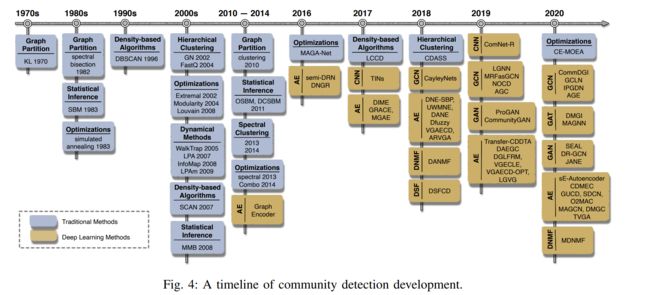
社区发现的发展：

传统方法在网络结构上进行社区发现，它们大致可以分为7类，但只能发现浅层关联，因此结果往往是次优的。而基于深度学习的社区发现方法可以发现深层的网络信息和复杂的关系、处理高维数据。

传统社区发现方法与基于深度学习的社区发现方法：

发展历史：

七类传统方法：

图划分(Graph Partition):
此类方法也被称为图聚类，它将网络划分为 k 个社区。社区内的边要比社区之间的边更为稠密。代表性的算法包括：Kernighan-Lin 启发式方法、谱二分法等。此类方法在深度学习方法中仍然被使用。

统计推断(Statistical Inference)：
代表性的算法为随机块模型（SBM），这是一类被广泛使用的生成式模型，它将节点分配到社区中，并控制它们的似然概率。其变体包括：DCSBM、MMB、OSBM等。

层次聚类(Hierarchical Clustering)：
此类方法通过分裂式、凝聚式和混合式三种方式发现不同层次上的社区结构。Girvan-Newman（GN）算法通过分裂式方法依次删除网络中的边从而发现新的社区，输出一种关于社区结构的层次化树状表征。FastQ(FN算法)是一种凝聚式算法，它逐渐将节点合并为一个社区。CDASS 算法同时应用了分裂式和凝聚式策略，基于结构相似度对图进行划分，并将其合并为层次化的社区。

动力学方法(Dynamical Methods)：
随机游走利用随机游走器在一段较短的游走中陷入某个社区的趋势，是最常被用于社区发现任务的动力学方法。代表性的算法包括：WalkTrap（使用随机游走计算社区内测量接地那相似性的概率和距离）、InfoMap（利用最小长度编码描述随机游走的路径检测社区）、LPA（通过信息传播机制来识别社区）、LPAm（LPA与模块度结合）。

谱聚类(Spectral Clustering)：
网络的谱属性可以被用于社区发现任务。谱聚类基于网络的正则化邻接矩阵的归一化拉普拉斯矩阵划分节点，并且使用伪似然算法将划分结果拟合到 SBM 算法上。

基于密度的方法(Density-based Algorithms)：
此类方法的代表性算法包括：DBSCAN、SCAN、LCCD。它们通过测量实体密度来确定社区、中心和异常。LCCD特别使用密度峰值聚类算法从网络中定位结构中心，然后通过局部搜索过程将社区从确定的中心扩展到边界。

优化方法(Optimizations)：
社区发现方法利用优化算法来达到某个极值，通常期望表明社区的似然。最经典的优化函数为Modularity(Q) 及其变体FastQ，它被用来估计网络划分得到的社区结构。Louvain是另一种著名的优化算法，它采用节点移动策略提取具有更大网络模块度的社区结构。此外，贪婪优化方法还包括模拟退火、极值优化、以及谱优化。演化社区发现方法在局部学习和全局搜索中十分有效，它分为单目标优化和多目标优化。多智能体遗传算法（MAGA-Net）等单目标优化算法利用了模块度函数，而 Combo等算法则融合了归一化互信息(NMI)、Conductance(CON)在内的多个优化目标。CE-MOEA 算法基于非支配排序遗传算法（NSGA-II）来优化模块度和相似性目标。

为什么需要深度学习进行社区发现？ 特别是在大型复杂网络中，深度学习模型具有利用节点、邻域、边、子图等的高维非线性特征（即网络拓扑信息）和高维关系特征（即网络属性信息）并对特征进行编码的优势。 这样的模型对稀疏网络更具弹性，并且更适合现实世界场景中的无监督学习任务。

深度学习社区发现的分类：

本文提出了一个针对基于深度学习的社区发现方法的分类框架。该框架将相关方法总结为六类：卷积网络、图注意力网络 (GAT)、生成对抗网络 (GAN)、自编码器 (AE)、深度非负矩阵分解 (DNMF) 和深度稀疏过滤 (DSF)。卷积网络包括卷积神经网络（CNN）和图卷积网络（GCN）。AE 进一步分为堆叠 AE、稀疏 AE、去噪 AE、图卷积 AE、图注意力 AE 和变分 AE (VAE) 等子类别。

基于卷积网络的社区发现：

卷积神经网络（CNN）是一种针对网格式拓扑数据，如图像数据，而提出的前馈深度神经网络（DNN），其中卷积层降低了计算成本，而池化操作保证了 CNN 在特征表达上的鲁棒性。图卷积网络（GCN）是基于CNN 和图的局部谱滤波器的一阶近似而提出的用于图结构数据的卷积网络模型。GCN中使用的传播规则设计为：
$$H^{(l+1)}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$
其中，$H^{(l)}$ 通过激活函数$\sigma (\cdot )$ 和层特定的可训练权重矩阵$W^{(l)}$保留第$l层中的潜在表示矩阵(H^{(0)}=X)；\tilde{A}=A+I_n为无向图G加入自连接后的邻接矩阵，I_n是单位矩阵；{\tilde{D}}_{ii}={\sum }_j{\tilde{a}}_{ij}，其中{\tilde{a}}_{ij}\in \tilde{A}。$

基于CNN的社区发现:

现有的基于CNN的社区发现方法具有严格的数据输入限制：需要是图像格式数据和带标签数据。 因此，这些方法需要对其输入进行预处理：（1）将网络样本映射为图像数据格式，以及（2）提前手动标记节点或社区，因为大多数现实世界的网络没有标签。 下图展示了基于 CNN 的社区发现方法的通用框架：

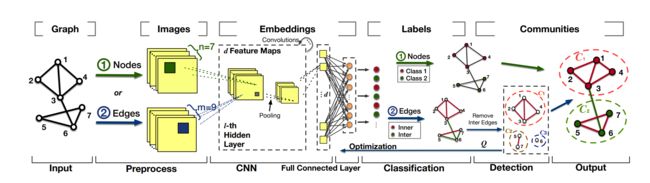
由于CNN模型通常仅处理图像数据(image)，当输入数据为图(graph)时，必须根据节点或边对数据进行预处理。总体框架中，CNN的隐藏层可以对数据的d维潜在特征进行卷积映射，接下来，由全连接层输出每个节点或每条边的表示以进行社区的分类。根据节点进行数据预处理时，图中的工作流①将节点分类为k类(即k个社区)，具有相同标签的节点会被划分到同一个社区中;根据边进行数据预处理时，工作流②将边分为两类——社区内与社区间的边。训练过程中，通过删除社区间的边形成社区结构，并通过反向传播到CNN嵌入中进行优化，从而得到最佳的社区划分结果，如模块度Q。

基于GCN的社区发现：

GCN在深度图卷积层中聚合节点的邻域信息，从而可以从全局捕获用于社区发现的复杂特征。基于GCN的社区发现方法有两类：(1)监督/半监督社区分类；(2)基于无监督网络表示的社区聚类。社区分类方法受到现实世界中缺乏标签的限制，相比之下，网络表示方法通过矩阵重构和目标优化等技术更灵活的聚类社区。下图展示了GCN通常如何应用于社区发现。

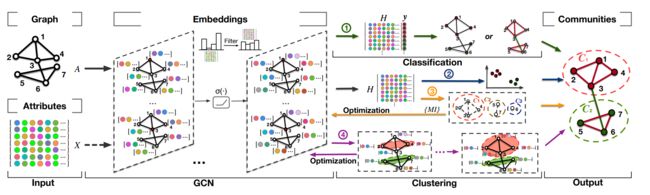
一个基于GCN的社区检测的通用框架。它输入一个图结构(A)和可能的节点属性(X)。在多个图卷积网络(GCN)层中，基于社区检测要求来平滑图的潜在特征(信息聚合)。图表示学习是通过σ(·)作激活函数的。四个社区检测框架在工作流①-④中，应用最终的节点表示(①和②)或隐藏层的特征表示(③和④)。①基于给定节点的标签，使用节点分类检测社区，②通过嵌入(H)对节点实现聚类，③中通过评估（例如互信息MI）进一步优化节点表示，以获得最佳的社区关系。④同时优化聚类结果和GCN表示，根据卷积表示节点嵌入，逐步将每个节点检测到社区中。

下表对比了一些基于GCN的方法。

基于图注意力网络GAT的社区发现：

基于图注意力网络（GAT）的社区发现方法可以发现复杂网络场景中的社区。框架如下图所示：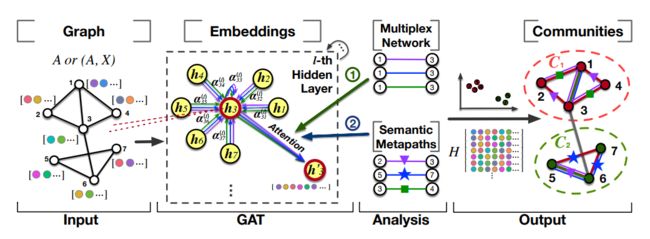
GAT在每个隐藏层I中为每个节点及其相邻的节点之间分配注意力系数(图中绿色，蓝色，紫色的箭头所示)。不同工作流所代表的向量分别聚合了所有的可用星系：①多层网络中同一对节点之间的多种关系；②异构网络中的语义路径。通过将社区结构分析嵌入到GAT表示汇总，将输出嵌入H应用于社区发现。

基于生成对抗网络GAN的社区发现：

对抗性训练在生成模型中是有效的，可以提高判别能力，但在应用于社区发现时需要解决过拟合问题。 生成对抗网络 (GAN) 在对抗训练中，在生成器${\varphi }_g$和判别器${\varphi }_d$之间进行竞争。 表示输入${\varphi }_d(x)$数据的概率，而 ${\varphi }_g$(z)学习生成器在输入噪声变量 $p_z(z)$上的数据 x上的分布 $p_g$。生成器通过生成假样本来欺骗鉴别器。其目标函数定义为：

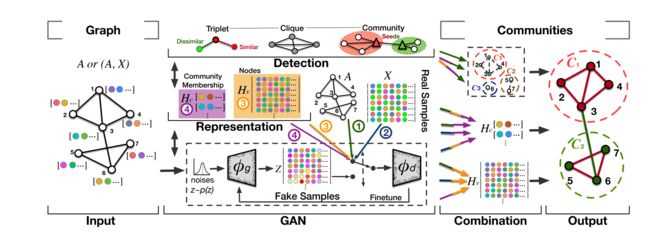
基于GAN的社区发现总体框架。在基于GAN的社区发现方法中，GAN通过生成器生成人造样本来欺骗判别器，判别器将多层感知机、图神经网络等深度神经网络作用于表征上。因此，真实样本和人造样本会通过竞争博弈进行调优，从而得到最优的社区特征。GAN中使用的真实样本包括:①拓扑结构A;②)拓扑结构与节点属性(A，X);③节点嵌入;④节点的社团归属。网络的拓扑结构以三元组、派系、社区等形式在表征或GAN模型中得到分析。这类方法能够在融合网络拓扑、属性和表征的过程中发现社区。

基于自编码器AE的社区发现：

自编码器(AE)是最常被用于无监督社区发现的模型，社区发现中常见的AE变体包括堆叠AE、稀疏AE、去噪AE、卷积AE、变分AE。AE 能够描绘非线性、有噪声的现实世界网络并产生平滑的表示。AE的通用框架由编码器$Z={\varphi }_r(A,X)$和解码器$X^{\prime }={\varphi }_r(Z)$构成。编码器 ( ${\varphi }_e$) 将高维网络结构 ( A ) 和可获取的属性 (X) 映射到低维潜在特征空间 (Z)。解码器 (${\varphi }_r$) 则根据编码器得到的表示 (H) 进行网络重构 (Z )，其中 X’继承了 A和 X中的首选信息。损失函数$L(x,{\varphi }_r({\varphi }_e(x))$ 最大化源数据x 和解码数据 ${\varphi }_r({\varphi }_e(x))$之间的似然。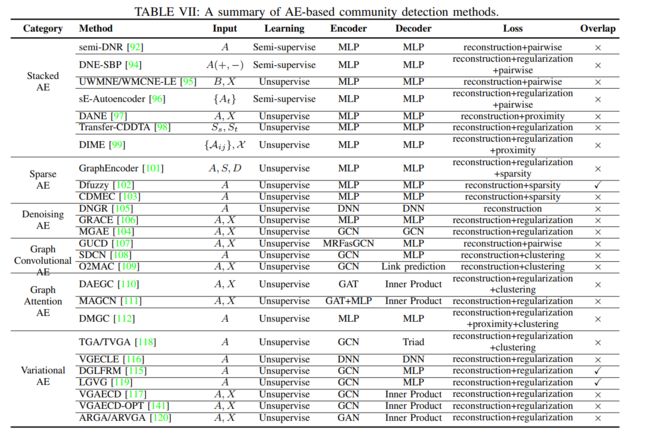
基于堆叠自编码器的社区发现：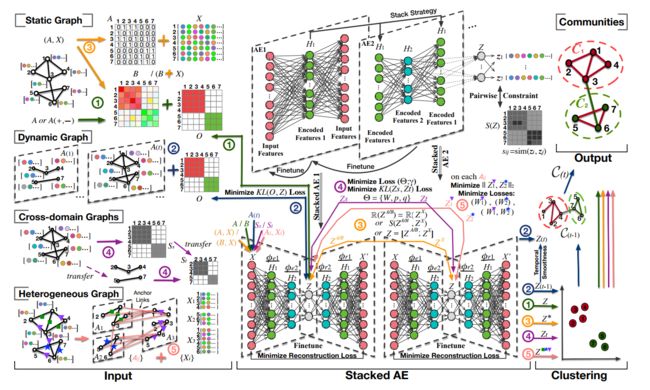
基于堆叠AE的社区发现总体框架。堆叠AE在多个隐层中将一组AE堆叠起来，以更加灵活地处理丰富的输入。我们在静态图、动态图.
跨域图、异构图中，分别考虑各种社区信息(A:邻接矩阵;A(+，-):带符号邻接矩阵; X:节点属性; B:模块度矩阵; O:节点对社区归属的先验信息矩阵; S︰节点对相似矩阵; {Aij}:锚链接矩阵）的5个代表性工作流，5种工作流都使用了成对约束和重建损失优化。在工作流①中，其输入为拓扑结构（(A或B)，优化重建损失和KL损失，输出最终用于节点聚类的嵌入Z。在工作流②中，输入为动态图的快照（At)，然后使用与工作流①中相同的堆叠AE嵌入过程。基于当前嵌入(Zt)和前一时刻嵌入(Z(t-1)的时序平滑性进行聚类，从而集成与前一时刻社区C(t-1)相似的当前社区结构Ct。在工作流③中，输入为拓扑结构(A或B)和节点属性 (X)，使用两个堆叠AE对这些属性进行表征，并同时使用重建损失优化由拓扑结构得到的嵌入和由节点属性得到的嵌入($Z^{A/B},Z^X$)。在工作流④中，将源域节点对的相似度信息迁移到目标域中。为了分析跨域的关系，通过同时在两个域上最小化可训练变量的损失，旨在最小化源域Zs,和目标域Zt嵌入的KL损失。因此，社区发现任务是在两个域的Zt编码图上进行的。在工作流⑤中，输入为不同元路径中对齐后的图，以及图i和图j之间的锚链接矩阵(Aij)。对于每一个Aij，最小化2-范数损失$||Z_1,Z_2|{|}_2$,和所有的损失都被赋予了堆叠AE权重。社区发现基于堆叠AE所得的嵌入进行聚类。

基于稀疏自编码器的社区发现：

稀疏性普遍存在于现实世界的网络中，并导致社区发现算法的计算困难。为了解决这一问题，稀疏 AE在隐藏层h中引入了稀疏惩罚$\Omega (h)$ 。重构损失函数如下：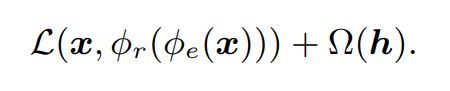
GraphEncoder (Autoencoder-based Graph Clustering Model) 是第一个使用 AE 进行图聚类的研究。 它通过作为以下损失函数（最小化）的一部分的稀疏项来处理稀疏性：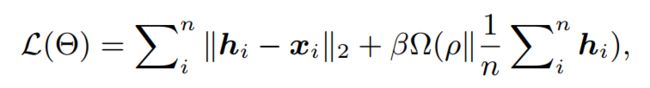
GraphEncoder 提高了大规模网络的聚类效率，并证明了稀疏网络可以为表示提供足够的结构信息。

CDMEC (Community Detection Method via Ensemble Clustering) 的社区发现方法将稀疏 AE 与迁移学习模型相结合，以从局部网络结构中发现更多有价值的信息。

Dfuzzy (Deep Learning-based Fuzzy Clustering Model)用于并行处理框架下稀疏大规模网络中的重叠社区发现。

基于降噪自编码器的社区发现:

降噪过程减去了 DNN 层内的噪声。 降噪 AE能够处理损坏的输入数据 ($\tilde{x}$) 并最小化去噪数据 (x ) 和解码数据之间的重构损失：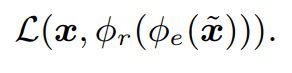
DNGR (Deep Neural Networks for Graph Representation)是在具有 3 个隐藏层的堆叠降噪自编码器框架中设计的。DNGR 应用堆叠降噪编码器来增加发现社区时捕获局部结构信息的鲁棒性。具体来说，它通过随机遍历社区来生成概率共现矩阵，并将其转换为移位的正逐点 MI 矩阵作为输入。

对于损坏的节点属性，GRACE (GRAph Clustering with dynamic Embedding)是一个非线性多层 DNN 的降噪 AE，由邻域内的影响传播引导，以发现动态变化的社区间活动，通过自训练聚类达到了有效的社区发现性能。

MGAE (Marginalized Graph AutoEncoder )对图的属性和结构进行降噪，以通过边缘化过程改进社区发现。它在 m 次内获得损坏的特征 $\tilde{X}$。MGAE训练中的目标函数定义为：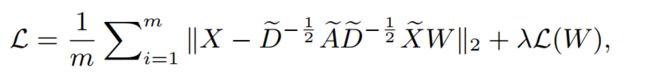
其中 L(W)表示系数为 $\lambda$的参数 W的正则化项。

基于卷积自编码器的社区发现:

将 GCN 引入 AE 是一个巨大的成功，因为 GCN 提供了高阶图正则化，而 AE 缓解了 GCN 中的过度平滑问题。 例如，基于 GCN 的无监督社区检测 (GUCD) 方法采用半监督 MRF 作为 GCN 中的卷积层（即MRFasGCN)作为其编码器，并提出了一种以社区为中心的双重解码器来检测属性网络中的社区。具体来说，GUCD使用一个解码器重构网络拓扑，另一个解码节点属性，以直接识别社区结构。

SDCN (Structural Deep Clustering Network)设计了一个传递算子来在 DNN 层上连接 AE 和 GCN，从而使图卷积可以完全支持 AE 的结构表示。当 SDCN 将结构信息集成到深度聚类中时，它通过分别对 AE 和 GCN 应用双重自监督优化来更新社区。

O2MAC (One2Multi Graph Autoencoder for Multi-view Graph Clustering 是一种针对多视图属性图的，由单视图到多视图 (One2Multi) 的图聚类 AE。它由一个编码器和多个解码器组成。在编码器中，应用 GCN 来嵌入一组视图分隔图。同时将解码器分别分配给这些单视图，并与编码器共同选择包含信息最多的单视图。O2MAC 能够捕获多视图之间的共享特征，并通过自训练优化改进聚类结果。

基于图注意力自编码器的社区发现:

该类别的社区发现方法不是集成 GCN，而是将 GAT 应用于 AE。DAEGC (Deep Attentional Embedded Graph Clustering) 采用 GAT 作为编码器对邻域内属性节点的重要性进行排序，利用高阶邻域来聚类社区。 多视图网络有两种基于 GAT 和 AE 的社区发现方法。MAGCN (Multi-View Attribute Graph Convolution Networks ) 设计了一个双路径编码器：第一个路径使用能够去噪的多视图属性 GAT 进行编码，第二个路径设计了一个编码器以在多视图属性上获得一致的嵌入。因此，MAGCN 为社区发现任务去除了噪声和分布方差。DMGC (Deep Multi-Graph Clustering)引入了 AE 来表示每个图的注意力系数，多个图的节点嵌入将通过跨图质心聚类以获得 Cauthy 分布上的社区。

基于变分自编码器的社区发现:

变分自动编码器（VAE）是基于变分推理（如特征的均值和协方差）的 AE 的扩展。它由变分图自编码器（VGAE） 首次引入图学习领域，它假设高斯分布并应用 GCN 作为编码器。基于 VAE 的社区发现由 SBM 等模型激活，以快速推断节点表示中的社区归属。推理过程考虑了网络的不确定性，例如连接多个社区的边界节点的邻居之间的社区矛盾。VAE 还可以处理社区发现的稀疏性问题。同时，VAE 很容易与更深层次的非线性关系信息相结合。例如，TGA/TVGA (Triad Variational Graph Autoencoder ) 用新的 triad 解码器替换了 VAE/VGAE 的解码器，它描述了现实世界的社区中现有的三元闭包属性。

基于深度非负矩阵分解的社区发现:

非负矩阵分解旨在将一个矩阵分解成两个小的非负矩阵，该方法具有高度的可解释性，能够发现如何将节点分配给社区。应用于社区发现的基本 NMF 模型将邻接矩阵 A) 分解为两个非负矩阵 ( $U\in R^{n\times k}和P\in R^{n\times k}$)，其非负约束为 $P\ge 0$ 和 $U\ge 0$ 。矩阵U 对应于原始网络和社区归属空间之间的映射。矩阵$P=[p_{ij}]$的每一列表示节点vi属于社区 cj的归属强度为概率 pij 。NMF 适用于非重叠和重叠的社区发现。由于现实世界的网络包含复杂的拓扑信息，传统的 NMF 无法完全揭示它们来检测社区。受深度学习成功的启发，人们对深度 NMF 进行了广泛的研究，它堆叠多层 NMF ( {$U_1,...,U_p$} ) 以捕获各个级别/方面的节点成对相似性.

基于稀疏滤波的社区发现:

稀疏滤波是一种简单的双层学习模型，它可以处理高维的图数据，将高度稀疏的输入表征为低维特征向量。高度稀疏的输入（具有很多 0 元素的 ）将被表示为低维特征向量（具有非零值的 ）。为了探索节点的社团归属等更深入的信息，深度SF将多个隐层堆叠起来，从而对更多超参数 ( $\Theta$) 和大量的平滑数据分布($Pr(h_i)$ )进行调优。

DSFCD (Community Discovery based on Deep Sparse Filtering) 作为一种代表性的方法，可以分为三个步骤：网络表示、社区特征映射和社区发现。 网络表示阶段分别在邻接矩阵 ( A)、模块度矩阵 (B ) 和两个相似性矩阵 (S 和 S") 上执行。选择最佳表示输入到深度 SF 中，以获得在每个节点上表示的社区特征映射(hi ) 。同时， 保留了原始网络( A)中的节点相似性和潜在社区归属特征。节点成对约束在损失函数中建模：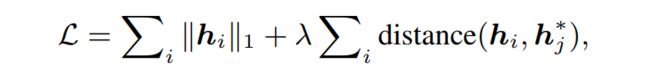
其中$||\cdot |{|}_1$是优化稀疏度的L1范数惩罚， $h_j^{\ast }$为节点 的最相似表示，通过在 Euclidean 或 KL 上计算 distance(hi,hj)距离得到。在最小化损失上优化学习过程中，相似的节点会聚集到同一社区中。深度 SF 架构在现实世界数据集的实验中具有重要意义，DSFCD 能比 SF 更准确地发现社区结构。

数据集：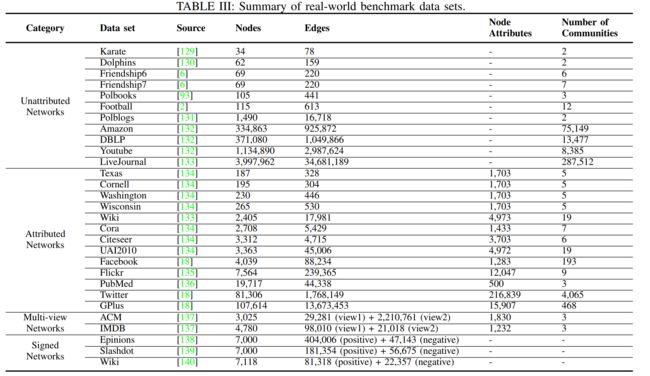

评价指标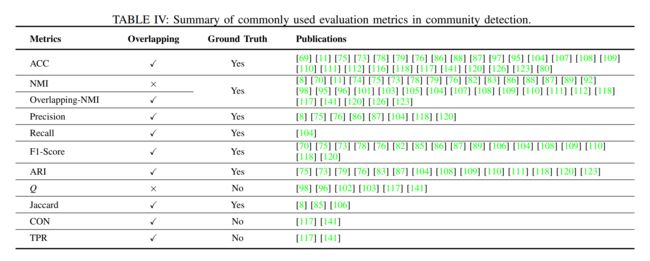

实际应用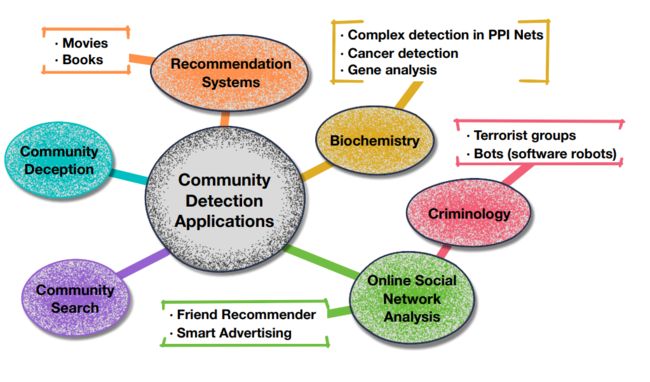

未来方向：

未知的社区数量

社区嵌入

层次化网络

多层网络

异构网络

网络异质性

拓扑不完备的网络

跨域网络

多属性视图网络

带符号的网络

动态网络

大规模网络