周志华《机器学习》第三章课后习题
目录
3.1 试析在什么情形下式(3.2) 中不必考虑偏置项 b.
3.2、试证明,对于参数w,对率回归的目标函数(3.18)是非凸的,但其对数似然函数(3.27)是凸的.
3.3、编程实现对率回归,并给出西瓜数据集3.0α上的结果.
3.4 选择两个 UCI 数据集,比较 10 折交叉验证法和留一法所估计出的对率回归的错误率。
3.5 编辑实现线性判别分析,并给出西瓜数据集 3.0α 上的结果.
3.1 试析在什么情形下式(3.2) 中不必考虑偏置项 b.
①b与输入毫无关系,如果没有b,y‘=wx必须经过原点
②当两个线性模型相减时,消除了b。可用训练集中每个样本都减去第一个样本,然后对新的样本做线性回归,不用考虑偏置项b。
3.2、试证明,对于参数w,对率回归的目标函数(3.18)是非凸的,但其对数似然函数(3.27)是凸的.
3.27
3.3、编程实现对率回归,并给出西瓜数据集3.0α上的结果.
数据集:
3.3.py
# -*- coding: utf-8 -*
'''
data importion
'''
import numpy as np # for matrix calculation
import matplotlib.pyplot as plt
# load the CSV file as a numpy matrix
# 将CSV文件加载为numpy矩阵
dataset = np.loadtxt('watermelon3_0_Ch.csv', delimiter=",")
# separate the data from the target attributes
# 将数据与目标属性分离
X = dataset[:, 1:3]
y = dataset[:, 3]
m, n = np.shape(X)
# draw scatter diagram to show the raw data
#绘制出数据点
f1 = plt.figure(1)
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('ratio_sugar')
plt.scatter(X[y == 0, 0], X[y == 0, 1], marker='o', color='k', s=100, label='bad')
plt.scatter(X[y == 1, 0], X[y == 1, 1], marker='o', color='g', s=100, label='good')
plt.legend(loc='upper right')
# plt.show()
'''
using sklearn lib for logistic regression
使用sklearn库进行逻辑回归
'''
from sklearn import metrics
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
import matplotlib.pylab as pl
# generalization of test and train set
# 先划分训练集和测试集,采用sklearn.model_selection.train_test_split()实现
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.5, random_state=0)
# model training
# 采用sklearn.linear_model.LogisticRegression,基于训练集直接拟合出逻辑回归模型,然后在测试集上评估模型(查看混淆矩阵和F1值)
log_model = LogisticRegression() # using log-regression lib model
log_model.fit(X_train, y_train) # fitting
# model validation 模型确认
y_pred = log_model.predict(X_test)
# summarize the fit of the model 总结模型的拟合情况
print(metrics.confusion_matrix(y_test, y_pred))
print(metrics.classification_report(y_test, y_pred))
precision, recall, thresholds = metrics.precision_recall_curve(y_test, y_pred)
# show decision boundary in plt 在PLT中显示决策边界
# X - some data in 2dimensional np.array X -二维np.array中的一些数据
f2 = plt.figure(2)
h = 0.001
x0_min, x0_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
x1_min, x1_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
x0, x1 = np.meshgrid(np.arange(x0_min, x0_max, h),
np.arange(x1_min, x1_max, h))
# here "model" is your model's prediction (classification) function
# 这里的“模型”是模型的预测(分类)函数
z = log_model.predict(np.c_[x0.ravel(), x1.ravel()])
# Put the result into a color plot 把结果放入颜色图中
z = z.reshape(x0.shape)
# 采用matplotlib.contourf绘制的决策区域和边界,可以看出对率回归分类器还是成功的分出了绝大多数类:
plt.contourf(x0, x1, z, cmap=pl.cm.Paired)
# Plot also the training pointsplt.title('watermelon_3a')
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('ratio_sugar')
plt.scatter(X[y == 0, 0], X[y == 0, 1], marker='o', color='k', s=100, label='bad')
plt.scatter(X[y == 1, 0], X[y == 1, 1], marker='o', color='g', s=100, label='good')
# plt.show()
'''
coding to implement logistic regression
编码以实现逻辑回归
'''
from sklearn import model_selection
import self_def
# X_train, X_test, y_train, y_test
np.ones(n)
m, n = np.shape(X)
X_ex = np.c_[X, np.ones(m)] # extend the variable matrix to [x, 1]
X_train, X_test, y_train, y_test = model_selection.train_test_split(X_ex, y, test_size=0.5, random_state=0)
# using gradDescent to get the optimal parameter beta = [w, b] in page-59
beta = self_def.gradDscent_2(X_train, y_train)
# prediction, beta mapping to the model
y_pred = self_def.predict(X_test, beta)
m_test = np.shape(X_test)[0]
# calculation of confusion_matrix and prediction accuracy
# #混淆矩阵的计算和预测精度
cfmat = np.zeros((2, 2))
for i in range(m_test):
if y_pred[i] == y_test[i] == 0:
cfmat[0, 0] += 1
elif y_pred[i] == y_test[i] == 1:
cfmat[1, 1] += 1
elif y_pred[i] == 0:
cfmat[1, 0] += 1
elif y_pred[i] == 1:
cfmat[0, 1] += 1
print(cfmat)
self_def.py 是 需要调用的函数
import numpy as np
def likelihood_sub(x, y, beta):
'''
@param X: one sample variables
@param y: one sample label
@param beta: the parameter vector in 3.27
@return: the sub_log-likelihood of 3.27
3.27式子的变成对象
'''
return -y * np.dot(beta, x.T) + np.math.log(1 + np.math.exp(np.dot(beta, x.T)))
def likelihood(X, y, beta):
'''
@param X: the sample variables matrix
@param y: the sample label matrix
@param beta: the parameter vector in 3.27
@return: the log-likelihood of 3.27
'''
sum = 0
m, n = np.shape(X)
for i in range(m):
sum += likelihood_sub(X[i], y[i], beta)
return sum
def partial_derivative(X, y, beta): # refer to 3.30 on book page 60 请参阅第60页的3.30
'''
@param X: the sample variables matrix
@param y: the sample label matrix
@param X:样本变量矩阵
@param y:样本标签矩阵
@param beta: the parameter vector in 3.27
@return: the partial derivative of beta [j]
'''
m, n = np.shape(X)
pd = np.zeros(n)
for i in range(m):
tmp = y[i] - sigmoid(X[i], beta)
for j in range(n):
pd[j] += X[i][j] * (tmp)
return pd
def gradDscent_1(X, y): # implementation of fundational gradDscent algorithms 基本梯度算法的实现
'''
@param X: X is the variable matrix
@param y: y is the label array
@return: the best parameter estimate of 3.27
然后基于训练集(注意x->[x,1]),给出基于3.27似然函数的定步长梯度下降法,降低损失,注意这里的偏梯度实现技巧:
'''
import matplotlib.pyplot as plt
h = 0.1 # step length of iterator 迭代器的步长
max_times = 500 # give the iterative times limit 给出迭代次数的极限
m, n = np.shape(X)
b = np.zeros((n, max_times)) # for show convergence curve of parameter 表示参数的收敛曲线
beta = np.zeros(n) # parameter and initial 参数和初始
delta_beta = np.ones(n) * h
llh = 0
llh_temp = 0
for i in range(max_times):
beta_temp = beta.copy()
for j in range(n):
# for partial derivative 偏导数
beta[j] += delta_beta[j]
llh_tmp = likelihood(X, y, beta)
delta_beta[j] = -h * (llh_tmp - llh) / delta_beta[j]
b[j, i] = beta[j]
beta[j] = beta_temp[j]
beta += delta_beta
llh = likelihood(X, y, beta)
t = np.arange(max_times)
f2 = plt.figure(3)
p1 = plt.subplot(311)
p1.plot(t, b[0])
plt.ylabel('w1')
p2 = plt.subplot(312)
p2.plot(t, b[1])
plt.ylabel('w2')
p3 = plt.subplot(313)
p3.plot(t, b[2])
plt.ylabel('b')
plt.show()
return beta
'''
采用随机梯度下降法来优化:上面采用的是全局定步长梯度下降法(称之为批量梯度下降),
这种方法在可能会面临收敛过慢和收敛曲线波动情况的同时,每次迭代需要全局计算,
计算量随数据量增大而急剧增大。所以尝试采用随机梯度下降来改善参数迭代寻优过程。
'''
def gradDscent_2(X, y): # implementation of stochastic gradDscent algorithms 随机梯度算法的实现
'''
@param X: X is the variable matrix
@param y: y is the label array
@return: the best parameter estimate of 3.27
随机梯度下降法的核心思想是增量学习:一次只用一个新样本来更新回归系数,从而形成在线流式处理。
同时为了加快收敛,采用变步长的策略,h随着迭代次数逐渐减小。
'''
import matplotlib.pyplot as plt
m, n = np.shape(X)
h = 0.5 # step length of iterator and initial
beta = np.zeros(n) # parameter and initial
delta_beta = np.ones(n) * h
llh = 0
llh_temp = 0
b = np.zeros((n, m)) # for show convergence curve of parameter
for i in range(m):
beta_temp = beta.copy()
for j in range(n):
# for partial derivative
h = 0.5 * 1 / (1 + i + j) # change step length of iterator
beta[j] += delta_beta[j]
b[j, i] = beta[j]
llh_tmp = likelihood_sub(X[i], y[i], beta)
delta_beta[j] = -h * (llh_tmp - llh) / delta_beta[j]
beta[j] = beta_temp[j]
beta += delta_beta
llh = likelihood_sub(X[i], y[i], beta)
t = np.arange(m)
f2 = plt.figure(3)
p1 = plt.subplot(311)
p1.plot(t, b[0])
plt.ylabel('w1')
p2 = plt.subplot(312)
p2.plot(t, b[1])
plt.ylabel('w2')
p3 = plt.subplot(313)
p3.plot(t, b[2])
plt.ylabel('b')
plt.show()
return beta
#sigmoid函数
def sigmoid(x, beta):
'''
@param x: is the predict variable
@param beta: is the parameter
@return: the sigmoid function value
'''
return 1.0 / (1 + np.math.exp(- np.dot(beta, x.T)))
def predict(X, beta):
'''
prediction the class lable using sigmoid 使用sigmoid预测类标签
@param X: data sample form like [x, 1] 数据样本形式如[x, 1]
@param beta: the parameter of sigmoid form like [w, b] 形如[w, b]的参数
@return: the class lable array 类标签数组
'''
m, n = np.shape(X)
y = np.zeros(m)
for i in range(m):
if sigmoid(X[i], beta) > 0.5: y[i] = 1;
return y
return3.4 选择两个 UCI 数据集,比较 10 折交叉验证法和留一法所估计出的对率回归的错误率。
参考代码: han1057578619/MachineLearning_Zhouzhihua_ProblemSets
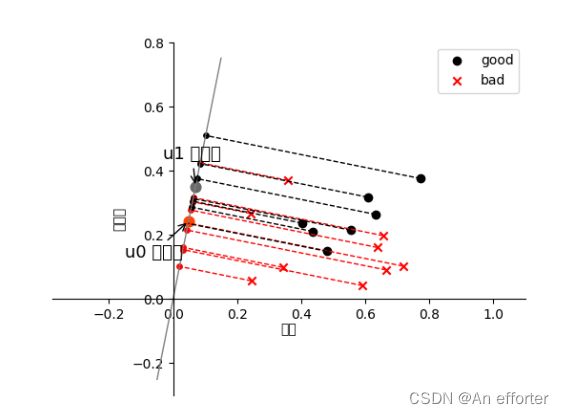
3.5 编辑实现线性判别分析,并给出西瓜数据集 3.0α 上的结果.
3.5.py
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
class LDA(object):
# 绘图,求出均值向量,根据公式3.34和3.39求出类内散度矩阵和类间散度矩阵
def fit(self, X_, y_, plot_=False):
pos = y_ == 1
neg = y_ == 0
X0 = X_[neg]
X1 = X_[pos]
# 均值向量,(1, 2)
u0 = X0.mean(0, keepdims=True) # (1, n)
u1 = X1.mean(0, keepdims=True)
# 类内散度矩阵,公式3.33,(2, 2)
sw = np.dot((X0 - u0).T, (X0 - u0)) + np.dot((X1 - u1).T, (X1 - u1))
# 类间散度矩阵,公式3.37,(1, 2)
w = np.dot(np.linalg.inv(sw), (u0 - u1).T).reshape(1, -1)
if plot_:
fig, ax = plt.subplots()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['left'].set_position(('data', 0))
ax.spines['bottom'].set_position(('data', 0))
plt.scatter(X1[:, 0], X1[:, 1], c='k', marker='o', label='good')
plt.scatter(X0[:, 0], X0[:, 1], c='r', marker='x', label='bad')
plt.xlabel('密度', labelpad=1)
plt.ylabel('含糖量')
plt.legend(loc='upper right')
x_tmp = np.linspace(-0.05, 0.15)
y_tmp = x_tmp * w[0, 1] / w[0, 0]
plt.plot(x_tmp, y_tmp, '#808080', linewidth=1)
wu = w / np.linalg.norm(w)
# 正负样板店
X0_project = np.dot(X0, np.dot(wu.T, wu))
plt.scatter(X0_project[:, 0], X0_project[:, 1], c='r', s=15)
for i in range(X0.shape[0]):
plt.plot([X0[i, 0], X0_project[i, 0]], [X0[i, 1], X0_project[i, 1]], '--r', linewidth=1)
X1_project = np.dot(X1, np.dot(wu.T, wu))
plt.scatter(X1_project[:, 0], X1_project[:, 1], c='k', s=15)
for i in range(X1.shape[0]):
plt.plot([X1[i, 0], X1_project[i, 0]], [X1[i, 1], X1_project[i, 1]], '--k', linewidth=1)
# 中心点的投影
u0_project = np.dot(u0, np.dot(wu.T, wu))
plt.scatter(u0_project[:, 0], u0_project[:, 1], c='#FF4500', s=60)
u1_project = np.dot(u1, np.dot(wu.T, wu))
plt.scatter(u1_project[:, 0], u1_project[:, 1], c='#696969', s=60)
# 均值向量的投影点
ax.annotate(r'u0 投影点',
xy=(u0_project[:, 0], u0_project[:, 1]),
xytext=(u0_project[:, 0] - 0.2, u0_project[:, 1] - 0.1),
size=13,
va="center", ha="left",
arrowprops=dict(arrowstyle="->",
color="k",
)
)
ax.annotate(r'u1 投影点',
xy=(u1_project[:, 0], u1_project[:, 1]),
xytext=(u1_project[:, 0] - 0.1, u1_project[:, 1] + 0.1),
size=13,
va="center", ha="left",
arrowprops=dict(arrowstyle="->",
color="k",
)
)
plt.axis("equal") # 两坐标轴的单位刻度长度保存一致
plt.show()
self.w = w
self.u0 = u0
self.u1 = u1
return self
def predict(self, X):
project = np.dot(X, self.w.T)
wu0 = np.dot(self.w, self.u0.T)
wu1 = np.dot(self.w, self.u1.T)
return (np.abs(project - wu1) < np.abs(project - wu0)).astype(int)
if __name__ == '__main__':
data_path = r'watermelon3_0_Ch.csv'
data = pd.read_csv(data_path).values
X = data[:, 1:3].astype(float)
y = data[:, 3]
y[y == '是'] = 1
y[y == '否'] = 0
y = y.astype(int)
lda = LDA()
lda.fit(X, y, plot_=True)
print(lda.predict(X)) # 和逻辑回归的结果一致
print(y)
想要代码与数据资源的,可以加我微信好友
![]()
参考的博客:
(4条消息) 周志华《机器学习》课后习题第三章解答:Ch3.3 - 编程实现对率回归_zhangriqi的博客-CSDN博客
周志华《机器学习》课后习题(第三章):线性模型-阿里云开发者社区 (aliyun.com)