多元线性回归：客户价值预测

多元线性回归的原理与一元线性回归的原理区别在于有多个因素对目标变量产生影响，广泛运用于商业数据分析中。

01 ​数学原理

多元线性回归模型表达式如下：

        其中，、、 ......为不同特征变量，、、 ......为特征变量系数，为常数。多元回归模型的搭建是通过数学公式计算而获取合适的系数，使得如下公式的残差平方和最小，其中为实际值，为预测值。

 02 ​模型搭建

核心代码与一元线性回归一致，具体如下：

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X, Y)

 上述代码与一元线性回归代码的区别在于X包含了多个特征变量。

“ 多元线性回归的原理与一元线性回归的原理区别在于有多个因素对目标变量产生影响，广泛运用于商业数据分析中。”

03 案例：客户价值预测

1. 应用背景

    本案例预测信用卡用户的客户价值，主要是通过【'历史贷款金额', '贷款次数', '学历', '月收入', '性别'】这五个因素进行预测其价值，然后再根据其价值，后续在进行营销、服务、催收、产品咨询等方面业务时，工作人员可区别于普通客户对高价值客户进行服务，从而进一步挖掘其价值，并提高他们的忠诚度。

2.读取数据

    通过以下代码，读取之前已准备好的数据。

# 2.读取数据
import pandas as pd
df = pd.read_excel('客户价值数据表.xlsx')
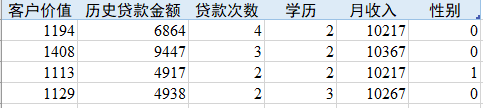
df.head()  # 显示前5行数据

显示前五行数据如下。“客户价值”列仅为1年的客户价值，“学历”列已做过预处理，其中2、3、4分别表示高中学历、本科学历、硕士学历。“性别”中0和1分别表示女性、男性。“客户价值”是因变量，第2至6列均为自变量。

3. 模型搭建

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X, Y)

4. 线性回归方程构造

regr.coef_

5. 运行结果

则多元线性回归模型表达式如下：

6. 模型预测

import statsmodels.api as sm  # 引入线性回归模型评估相关库
X2 = sm.add_constant(X)
est = sm.OLS(Y, X2).fit()
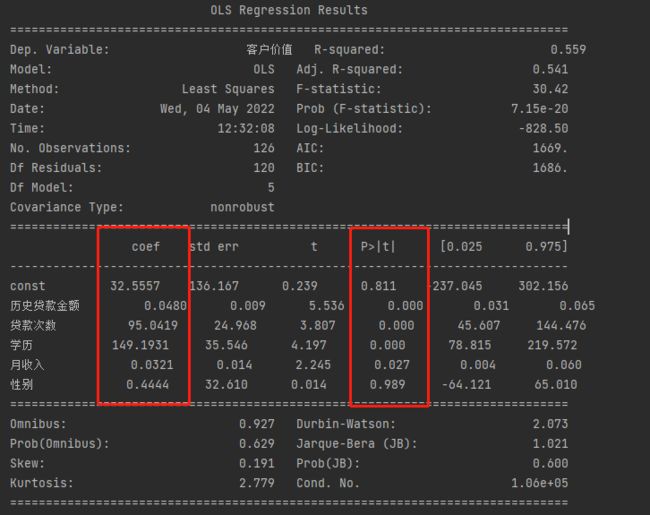
print(est.summary())

​

通过上图可以看出，由于数据量较少的原因，R-squared的值只有0.559，Adj.R-squared的值只有0.541，整体拟合效果并不理想。再来看P值，“性别”的P值最大，达到0.989，与目标变量没有显著相关，这个结论告诉我们，在之后的建模中，“性别”这一变量影响可以忽略不计，故而专门针对女性设计“女神卡”（只能女性申请的卡种）这一措施，对于挖掘客户价值的没有太大的意义​。

7. 本案例的缺陷
本案例是在已知客户价值的前提下进行建模的，如果未知客户价值的前提下，则需要使用非监督机器学习算法，此时不能直接预测客户价值，需要先使用K-means聚类算法对客户进行分群处理。