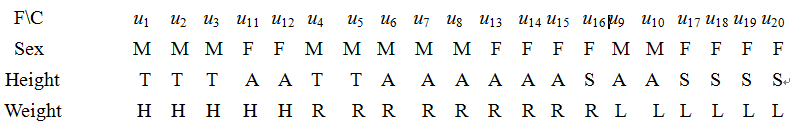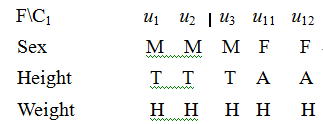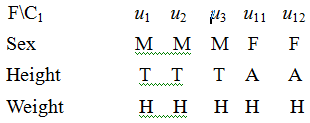Cognition math based on Factor Space (2016.05)

Cognition math based on Factor Space 

Wang P Z¹, Ouyang H², Zhong Y X³, He H C⁴

¹Intelligence Engineering and Math Institute, Liaoning Technical Univ. Fuxin, Liaoning, 123000, China

²Jie Macroelectronics co. Ltd, Shanghai, 200000, China

³ I & CE College, Beijing University of Posts and Telecommunication, Beijing 10080, China.

⁴Computer College, North-west Polytechnical University. Xi'an, 71072, China

 

Abstract The core of big data is intelligence still. Facing the challenge of big data, AI needs a deep and united theory, especially, a deep and united cognition math. There were three branches of cognition math emerging in 1982. One of them is Factor space theory initiated by the first author. Factor is fact-or, i.e. the initiator of fact, the quality-root of things, which is the generalization of gene. Factor space is the coordinate space with dimensions named by factors, which is generalization of Cartesian coordination for describing things and thinking. The paper introduces how to emulate cognition functions by factor space and how clear and pertinent the emulation is. Four simple and fast algorithms are presented. Based on factor space, the cognition packet is built as the basic unit in factor databases. Different from the existent data processing, factor databases are built by cultivation, whose target is cultivating the sample S of background relation R to emulate R. With the lapse of time, the background sample S becomes more mature and stable. Once the S equals to R, cognition packet will have the whole correct knowledge. Maintaining such a powerful function for big data, factor databases can employ background base to drastically compress data without information loss. As for the existent data processing frightened by the multi-challenge of big data, factor space theory brings us a sedative. The tide of big data will be tamed in factor databases. The cultivation is easy to be made since the sample of background relation don't concern about privacy. The bottlenecks caused by big data can be overcome by factor space theory. Factor space is the best framework for cognition math.

                      Keywords Factor space · Cognition Math · Factor databases · Man-machine cognition networks

                     Mathematics Subject Classification 90C05

1. Introduction

Big data is the era we are faced with, the character of big data is I & I, Internet and Intelligence. Internet is the wing and intelligence is the soul of information revolution^[1,2]. Big data era is not beyond, but in the historical stage of information revolution, and the core of big data is intelligence still. However, big data is a new stage at the internet time. When all computers communicate each other on line, what is the kind of computer like? The role of the CPU of the computer has been marginalized and the data processing software plays the main role of AI. The entity of AI machine, so called the fifth or post-fifth generation computer, will be replaced by the man-machine cognition network^[3]; the mode of AI will be changed from the bottom-top manual work to the combination of top-bottom and bottom-top network; which makes the man-machine cognition network intelligently huff ‘n’ puff big data from internet.  

Different from human intelligence, the subject of AI is not brain, but machine. How do machine emulate intelligence of brain? Is it possible to construct a brain-like machine? No matter how advanced science becomes, it is not possible to make a machine as a clone of brain. It is mystery that the insuperable barrier does not take away all belief from AI researchers. Even though the ebb of fifth generation computer in 1990s hints that computer must emulate from the structure of human brain, people still have confidence on AI facing the difficulty of structure-emulation. Indeed, we would cognize that brain is the cognition’s subject, but not the very cognition. Is there a cognition theory keeping a little independence from brain? It concerns with the relationship between cognition information and ontological information^[3]. Even though brain has influence to ontology information, ontology information is independent from the subject of cognition essentially, and there exists inner cognition theory to guide artificial intelligence. There were theories arising in artificial intelligences, unfortunately, they are not deep and united but shallow and split^[3,5]. There have been no deep and united artificial intelligence theory yet. No a strong theory, no substantial practice! Therefore, we are going to build a strong theory of artificial intelligence^[4,6].

Artificial intelligence can’t be achieved without mathematics. Existent heterogeneity of intelligence theory is caused by the heterogeneity of mathematics. To build a united information theory, we must to build a united cognition math.

What is cognition math? Cognition math is a branch of mathematics, which aims to mathematically research the cognition process. Cognition process includes three basic functions: 1. Concept generation; 2. Rule induction; 3. Logical inference. All other cognition functions are based on the three ones such as: Classification, Pattern recognition, Learning, Decision making, Evaluation, Curve fitting, Predication, Sentimental analysis, etc.

Was there cognition math we met before? Some papers call themselves the cognition math but may not be recognized by the world; while some mathematical branches having strong intelligent characters may not be recognized by themselves. Mathematical logic, probabilistic statistics, fuzzy sets theory, operational research and optimization etc., have strong intelligent characteristics; they do researches on the application spontaneously but not consciously for AI. They have not clearly declared that they are intelligence math. No matter in what cases, we need co-operation on building a cognition math, which collects all researches under a clear and united target on intelligence and cognition.

There were three mathematical branches emerging in 1982: Wille’s Formal Concept Analysis (FCA)^[7], Pawlak’s Rough Sets (RS)^[8] and Wang’s Factor Space (FS)^[9]. They are mathematical branches holding intelligent characteristics, and clearly declare that the object of mathematical description in branch is the knowledge and cognition. Based on the involution in between intension and extension, Wille gave a definition to concept mathematically. He wrote a book to discuss how to generate concept lattice (more clearly, the semi-lattice of basic concepts) from databases^[10]. He indeed opened up a precedent of cognitive mathematics. Wille’s work is rigorous; unfortunately, he emphasizes only attributes, which leads to great trouble in generating his formal background tables. The number of columns becomes to be exploding. The algorithms in formal concept analysis encounter N-hard complexity.

Instead of attributes, Pawlak emphasizes the ‘name of attributes’, and represents a family of attributes by one column in a tableau. Such an improvement saves a lot of columns, his information system becomes the general form of relational databases tableau. Rough sets theory establishes mathematical base for relational databases, which is a great contribution. Unfortunately, even though it employs the name of attributes, the authors have not recognized the importance of attribute name yet. A name of attributes is a factor, the keyword for information science. Rough sets had not given any introduction on factor and factors’ operations; while it uses factors’ operations in attribute reduction without clear mathematical statements. The algorithms of attribute reduction by rough set also meet trouble of N-hard complexity. 

Focusing on Wille’s background relation and Pawlak’s information system, FS helps FCA and RS to be deep and united. The cooperation of the three branches makes more simple and clear statements on basic problems in cognition science and obtains more simple and fast algorithms; the N-harp problems mentioned above can be resolved by at most O(m²n) complexity, where m, n are numbers of objects and factors respectively.

However, cognition math has been born. The new branches of cognition math are not limited in the three ones mentioned above, and the cooperation will be wider and wider.

The paper is organized as follows: Factor and factor space is introduced in Section 2; How to describe basic functions of cognition by factor space is introduced in Section 3; How to deal with uncertainty by factor space is introduced in Section 4; In Section 5, introduction of factor databases can be found, and the important points are data-cultivation, background base and man-machine cognition network. Finally, the conclusion is made in Section 6. 

 

2. Factor space

In the section, we will introduce what is factor and factor space. Factor is the quality-root of things, the commander of attributes, which is the keyword in the information and cognition science. Factor space is the coordinate space with dimensions named by factors, which is generalization of Cartesian coordination for describing things and thinking. The most important concept in factor space is background relation $R$, which is common platform of concept generation, rule extraction and inference. 

2.1 What is factor?

What is a factor? There are three dictionary explains: 1. Whole number (except 1), by which a larger number can be divided exactly; 2. Fact, helping to bring a result; 3. Agent, person who buys and sells commission. They are not exactly the meaning of factor in factor space theory, we need to explain in advance:

Factor is not the fact bring a result, but the initiator of the fact. Abundant rain is a fact bringing good harvest, which is a reason of good harvest but not a factor. The related factor is rainfall, which is variable, and causality occurs only in its variation. Suppose that the crop is kept in bumper no matter how varying the rainfall, then rainfall would not be the factor of good harvest. Rainfall was the main factor of good harvest in ancient agriculture because the variation of rainfall can change crop from bumper to no harvest. A factor is fact-or, which is not the fact, but the initiator of fact. From fact to factor, this is sublimation in brain’s cognition.

‘Abundant rain’ is an attribute in a district; while ‘rainfall’ is not an attribute, but the root of attributes. A factor bunches a group of attributes. In philosophy, quality and quantity are unity of opposites; philosophers value attribute since it describes quality. Unfortunately, few of them emphasize that: Attributes are not living alone but living in clan, and each clan includes at least two attributes. ‘Mamalian’ is an attribute of animal, which is not living alone, but companied by attribute ‘non-mammalian’. A family of attributes must have a common root, called quality-root by the author. Attributes will lose comparability if they are not in a same quality-root. Can we compare attributes ‘white’ and ‘heavy’? It is nonsense. It is only possible to make comparison, classification, concept-generation and knowledge-production for different attributes which are bunched on a same quality-root.

Without factor, like pearls will be scattered all over floor without bunch-line, attributes will be in disorder and exponential exploding. Brian is an optimized acceptor for information processing, it must be organized according to factors. Neurophysiology has proved this point.

Factor is the extractor of information. For example, when a man came to the shopping center, he should buy nothing if he did not know which kind of things he wants to buy. He loses the guiding of factor!

Without quality-root, we could not find out what is thing and what will be cognized. Philosophers have emphasized attributes already early, but neglect the quality-root still. In biology, gene is the quality-root of live attributes. It is the time to define factor as quality-root now. Factor is not only the initiator of fact bringing results, but also the initiator of things and cognition. In biology, gene once was called Mendel Factor, which means that gene is a special kind of factor; while factor is generalized gene. Gene is the unique keyword of biology, and factor will be the unique keyword of information and data science.

According to above analysis, we know that factor space grasps the most basic root of information and data science, and it provides a universal coordinate framework for descriptions of things and thinking.

Peoples confuse factor with attribute. They call color and red, green, yellow by a same word ‘attribute’. This is a big taboo in factor space. Color is a factor, which commands attributes red, green and yellow etc. Factor and attribute are in different levels. Attribute is intension of a concept with respect to a single factor, and the intension of a concept is attribute-configuration with respect to multiple factors. Don’t confuse factor with concept also. Concept needs to answer Y or N, but Y or N to a factor is non-sense. Is the meaning for Y or N to rainfall? Of course, in different contexts, factor and attribute may be interconvert-able, which is not a dogma. 

Factors in mathematics, is defined as a mapping, more specifically, a trait mapping, which maps things to their attributes or states.

Definition 1^[11]Mapping $f: U \to X(f)$ is called a factor on $U$. The domain $U$ is a set of things, objects or elements，called the universe of discussion; The co-domain $X(f)$ consists of objects' attributes, states or phases, called the phase space of $f$.

The name of trait mapping comes from quantitative trait locus (QTL) mapping in gene engineering. Which is called attribute mapping also by Feng J L in his attribute theory^[12]. His attribute mapping is the same as factor.

There are two types of phase spaces: quantitative and qualitative. Consider factor $f=$Height defined on a specific population and the quantitative phase space is $X(f)=[0.1, 2.5](m)$. In this case, a factor is a variable. The qualitative phase space is $X(f)={Short, Middle, High}$ and the phases are words in nature language and can be treated as fuzzy subsets of $X(f)$. How to transfer a quantitative phase space to a qualitative phase space or reverse? This is a basic problem of factor space and resolved by fuzzy sets or intuitive fuzzy sets theory. A qualitative phase space must not be a singleton, namely, the number of phases in a qualitative phase space m must be larger than 1, at least $m=2$. In this case, the factor is called a feature or characteristic. Feature is a special type of factor. The phase space of a feature consists of positive and negative states. Baby cognition starts from bi-phase factors usually. People naturally call the positive state as a feature sometimes. In this case, feature is not a factor but an attribute. We accept the two types of calling both, but distinguish the differences between them.

A quantitative phase space $X(f)$ can be integerized to a set of integers and we call it the carrier phase space.

Quality mapping determines a classification of universe $U$. Let f be a factor defined on $U$, which defines a equivalent relation $\sim$：For any $u, v\in U, u\sim v$ if and only if $f(u)=f(v)$. An equivalent relation determines a classification on $U$, set that

$$[u]_f={v\in U|f(u)=f(v)}, H(f,U)={[u]_f|u\in U}=U^*.$$  (1)

$H(f, U)$ is called the classification of $f$ on $U$.

According to the degree of thickness of classification, there are simple and complex factors. We call classification $H(f, U)$ is finer than $H(g, U)$, denoted $H(f, U)\succ H(g, U)$ if, for any class $[u]_g$, there is a class $[v]_f$ such that $[v]_f\subseteq[u]_g$.

Definition 2 We say that factor $f$ is more complex than factor $g$, denoted as $f\geq g$, if $H(f, U)\succ H(g, U)$. In this case, $g$ is called the sub-factor or lower factor of $f$, and $f$ is called the upper factor of $g$, denoted as $g\leq f$ .

2.2 Quantitative factor space

The statements on qualitative phase space is much difficult than quantitative space. We have to review the quantitative factor space firstly, and then introduce quantitative phase space. Quantitative factors space is ordinary Cartesian coordinate space. It includes time/space 4-dimensional space for description of particle movement, the phase space in physics, the state space in control systems, the diagnosis space in medical, the feature space in pattern recognition etc. which are all factor spaces. One of the newer points is that the dimension of a factor space is not fixed but variable. 

Example 1 Let $x_1, x_2$ and $x_3$ be variables describing left and right sides, top and bottom, front and behind, how to generate the three variables to be a variable dimension coordinates space?

Resolution Set $ F0={x_1, x_2, x_3}$。Denote that $f_1={x_1}, f_2={x_2}, f_3={x_3}, f_4={x_2, x_3}, f_5={x_1, x_3}, f_6={x_1, x_2}, f_7={x_1, x_2, x_3}, f_8={\emptyset}$. $F=P(F_0)$ forms a Boolean algebra. Viewing factor f as a parameter in the Boolean algebra, it becomes a variable dimension space. From fixed dimension to a variable dimension, this is a prime motive of factor space.

In linear space theory, a variable dimension is taken by bases of space. In example 1, let ${{\bf{e}}_1},{{\bf{e}}_2},{{\bf{e}}_3}$ be the unit vectors of axis $x_1, x_2, x_3$ respectively.While the coordinate space with respect to ${x_1, x_2}$ is the 2-dimensional plane generates by bases $e_1$ and $e_2$，i.e., $e_4={e_1,e_2}=e_1\cup e_2$. Similarly, we have that $e_5=e_1\cup e_3,e_6=e_2\cup e_3,e_7=e_1\cup e_2\cup e_3, e_4\cap e_5={e_1, e_2}\cap{e_1, e_3}=e_1, e_2^c={e_1, e_2, e_3}\setminus e_2={e_1, e_3}=e_5$ etc. The operations of factors can be described by operations of bases.

Factor is the perspective of cognition. In quantitative factor space, perspective is the bases of coordinate space. The compound of factors is the union of bases, which increases dimension and makes factor from simple to complex; the decomposition of factors is the intersection of bases, which decreases dimension and makes factor from complex to simple.

If two spaces having two groups of bases without common base, then the compound space is the Cartesian product of the two spaces. While, if the two group of bases have common base, the compounded space is not the Cartesian product of the two spaces. And we have known how to get the compounded space by existent theory. Unfortunately, we have no related theory for quality phase space since there is no base there. What we can do is give an axiomatic definition on qualitative factor space. 

2.3 Definition of factor space

Definition 3^[13] A factor space defined on universe of discussion $U$ is a family of sets ${\{ X(f)\} _{(f \in F)}}$ satisfying：

     （1）$F = (F, \vee , \wedge {,^c},{\bf{1}},{\bf{0}})$ is a complete Boolean algebra；

（2）$X(0) = \{ \emptyset \} $;

（3）For any $T \subseteq F$, if $\{ f|f \in T\} $ are irreducible (i.e., $s \ne t \Rightarrow s \wedge t = {\bf{0}}(s,t \in T)$), then

$X(\{ f|f \in T\} ) = {\Pi _{f \in T}}X(f)$ ($\Pi$ stands for Cartesian product);

（4）$\forall f \in T$, there is a mapping with same symbol $f:f \to X(f)$.

$F$ is called the set of factors, $f\in F$ is called a factor on $U$. $X(f)$ is called the phase space of factor $f$.

Definition 3' A factor space defined on $U$ is a regular factor space if $F$ is generated by a finite factor set ${F_0} = \{ {f_1}, \cdots ,{f_n}\} $, i.e., $F = P({F_0})$. The symbol of regular factor space can be simplified as $\psi  = (U:X({F_0}))$.

To be sure that $F_0$ may be and may not be the set of atom factors. i.e. it may be and may not be that ${f_i} \wedge {f_j} = {\bf{0}}$.

We only consider regular factor space in the paper, and we can replace the symbol $F_0$ by $F$. A regular factor space is simply denoted as $\psi  = (U:X(F))$, where $F = ({f_1}, \cdots ,{f_n})$, and for simplification, we denote that $F = ({f_1}, \cdots ,{f_n}) = {f_1} \vee  \cdots  \vee {f_n}$.

2.4 Background relation, the core of factor space

In the definition of factor space, the phase space of a synthesis factor may not be the Cartesian product of the phase space with respect to simple factors. Yes, it is, but the condition is that those simple factors have no common sub-factors, called irreducible. Now, the problem is：How do we do if they are reducible? We have had such an idea: No matter a group of factors irreducible or not, taking the Cartesian product of their phase space at first, and then considering the real configuration of phases, we get a very important concept defined as follows: 

Definition 4^[14] Given a regular factor space$\psi  = (U,X(F))$ with$F = ({f_1}, \cdots ,{f_n})$, for any ${\bf{a}} = ({a_1}, \cdots ,{a_n}) \in X = X({f_1}) \times  \cdots  \times X({f_n})$，denote that

$$[{\bf{a}}] = {F^{ - 1}}({\bf{a}}) = \{ u \in U|F(u) = {\bf{a}}\} $$. (2)

If $[{\bf{a}}] \ne \emptyset $，then a is called a intension atom; Else, a is a fictitious phase. The set of intension atoms

$$R = F(U) = \{ {\bf{a}} = ({a_1}, \cdots ,{a_n}) \in X|\exists u \in U,{f_1}(U) = {a_1}, \cdots ,{f_n}(u) = {a_n}\} $$ (3)

is called the background relation of  or the background set of $F$.

The background relation is the real Cartesian product of phase spaces. $R = X({f_1}) \times  \cdots  \times X({f_n})$ if and only if the group of factors are irreducible. Factors are irreducible if and only if their quality-roots are not intersected, the essential meaning of independent is empty-intersection of quality-roots. But, since the granule of quality-roots may be large, we do not dare to use quality-root to describe independence. However, independence implies that irreducible.

It is obvious that $F$ is isomorphism between $H(U, F)$ and $R$.

Background set $R$ is the generalized concept of formal background relation defined by Wille, it plays very important role in factor space.

3. Basic cognitive functions

In this Section, we will use background set, the common platform of intension and extension, to do concept generation, rule-extraction and inferences. Each one has a basic algorithm, based on which, cognition functions of brain can be emulated mathematically.

3.1. Concept generation

Concept is the unit of thinking. Concept-generation is the cell of cognition. A concept is defined by intension and extension. Intension logically states about its attributes and extension geometrically specifies its qualified entities. How to generate new concept by computer was an inconceivable problem and seemed with no start. Wille starts the task by defining a relation KÍU´A, where U and A are a finite set of objects and a finite set of attributes respectively. For any uÎU and aÎA, we say that object u holds attribute a if (u, a)ÎK. A tableau is called a formal background if it indicates the holding state of each pair (u_i, a_j), and K is called the formal background relation. For any VÍU and BÍA, denote that

f(V)={aÎA|"uÎV; (u, a)ÎK}; g(B)={uÎU|"aÎB; (u, a)ÎK}.

Wille defines that a pair a=(V, B) is called a concept if (V, B) satisfies involution principle^[7]:

g(f(V))=V (VÍU); f(g(B))=B (BÍA).

V and B are called its extension and intension respectively.

Wille presented methods of concept-generation. His work is rigorous; unfortunately, he emphasizes attributes but neglects the name of attributes, which made his formal background tables get into trouble. The number of columns becomes exploding. The algorithms in formal concept analysis encounter N-hard complexity.

The work of concept-generation done by factor space is very simple. The background set R is the set consist of intension a, and the classified universe U*=H(U, F) defined in (1) is the set consist of extension [a]. Since U* and R are isomorphism, U* can be represented by R, then R unifies intension and extension! The couple (a, [a]) must satisfy the involution principle.

Definition 5^[14]For any $a \in R,\alpha  = (a,[a])$ is called a atom concept with intension a and extension $[a]$. $\{ \alpha  = (a,[a])|a \in R\} $ is called the set of atom concepts. The Boolean algebra generated from atom concepts called the concept Boolean algebra.

Example 1 There is an universe $U$ with 20 persons. There are three factors Sex, Height and weight defined on $U$. A tableau, called factor tableau, records the attributes of each person with respect to three factors as follows:

 

We have that

X(S)={M，F}，X(Height)={Tall，Average，Short}，X(Weight)={Heavy，Regular，Light}.

According to Definition 4, we can get the background set according to Definition 4:

R={MTH, MTR, MAR, MAL, FAH, FAR, FSR, FSL}

U*={{u₁u₂ u₃},{u₄u₅},{u₆u₇ u₈},{u₉ u₁₀},{u₁₁u₁₂},{u₁₃u₁₄ u₁₅},{u₁₆},{u₁₇u₁₈ u₁₉ u₂₀}}

According to Definition 5, we can generate the set of atom concepts directly without any algorithm:

a₁=(MTH,{u₁u₂ u₃}), a₂=(MTR,{u₄u₅}), a₃=(MAR,{u₆u₇ u₈), a₄=(MAL,{u₉u₁₀}),

a₅=(FAH,{u₁₁u₁₂}), a₆=(FAR, {u₁₃u₁₄ u₁₅}), a₇=(FSR,{u₁₆}), a₈=(FSL,{u₁₇u₁₈ u₁₉ u₂₀}).

From the eight atom concepts, we can get 2⁸=256 concepts in the concept Boolean algebra. The number of generated concept is too big! We call a concept is basic if its intension can be written by conjunctive normal form, we consider basic concept only. Basic concept can be also defined as concept satisfying involution principle. Non-basic concepts do not satisfy such a principle. The intersection of basic concept is still a basic concept, all basic concepts consist a semi-lattice S. A problem is to find out the sub-lattice of S, which includes all atom concept and with the number of basic concept as small as possible. Factor space theory gives the basic algorithm as follows:

Definition 6^[14]Supposing that $H(U,F) = {\{ {C_k} = ({u_{k1}}, \cdots ,{u_{k,n(k)}})\} _{(k = 1, \cdots ,k)}}$，denote that

$${d_f} = 1 - \frac{{n(1)(n(1) - 1) +  \cdots  + n(K)(n(K) - 1)}}{{m(m - 1)}}$$ (5)

$d_f$ is called the distinguish degree of $ f$ with respect to $U$.

Background relation $R$ is the projection of formal background $K$ defined by Wille, which is the core concept in factor space theory.

Factor Space Algorithm 1 (Index-transposition)^[15]

          $C: = U$

    1. Calculating the distinguish degree of each factor in class $C$.

2. Selecting one factor $f$ having maximal distinguish degree, re-ordering the indices of objects in $C$ such that those who having same $f$-value are connected in one class.

         3. Tracing the first sub-class to repeat steps 1 and 2 until the traced sub-class could not be divided.

  4. Going to the next sub-class of the ending sub-class to repeat steps 1-3 until no class could not be divided. Stop.

5. Drawing the classification process as a tree, each node of the tree corresponding to a basic concept. The tree is called a graph of semi-lattice of basic concept.

In the algorithm, calculating distinguish degree of factors aims to shorten the number of node of the tree. Factor space aims to reduce the number of factors in use by extracting main factors.

Example 1(Continuing)

         $C: = U$

     1. Calculating the distinguish degree of each factor in class C.

           n=20;

          f₁=Sex，n(1)=10, n(2)=10, c_f1=1-(10´9+10´9)/20´19=1-180/380=1-9/19=10/19

f₂=Height，n(1)=5, n(2)=10, n(3)=5， c_f2=1-(5´4+10´9+5´4)/20´19=1-130/380=25/38

f₃=Weight，n(1)=5, n(2)=9, n(3)=6， c_f3=1-(5´4+9´8+6´5)/20´19=1-112/380=268/380

   2. Since f₃ has maximal distinguish degree in C, re-order indices in C such that classify C according to factor Weight:

                 $C = {C_1}\{ {u_1}{u_2}{u_3}{u_{11}}{u_{12}}\}  + {C_2}\{ {u_4}{u_5}{u_6}{u_7}{u_8}{u_{13}}{u_{14}}{u_{15}}{u_{16}}\}  + {C_3}\{ {u_{17}}{u_{18}}{u_{19}}{u_{20}}\} $

           According to the involution, they corresponding to three basic concepts ${\beta _1} = (Heavy,{C_1}),{\beta _2} = (Regular,{C_2}),{\beta _3} = (light,{C_3})$.

       3. Tracing ${C_1}$, the first sub-class of ${C}$. i. e. $C: = {C_1}$; Repeating step 1 and 2,

$n = 5$，

f₃=Weight n(1)=5, c_f3=1-(20´19)/20´19=0'

f₁=Sex，n(1)=3, n(2)=2, c_f1=1-(3´2+2´1)/5´4=1-8/20=12/20

f₂=Weight，n(1)=3, n(2)=2, c_f2=1-(3´2+2´1)/5´4=1-8/20=12/20

${c_{{f_1}}} = {c_{{f_2}}}$=maximum. Arbitrarily select one, Sex for example, to do classification. We get that

           ${C_1} = {C_{11}}\{ {u_1}{u_2}{u_3}\}  + {C_{12}}\{ {u_{11}}{u_{12}}\} $

According to the involution, they corresponding to three basic concepts ${\beta _{11}} = (HM,{C_{11}}),{\beta _{12}} = (HF,{C_{12}})$.

C₁₁ is not possible to be divided since the objects in the subclass have same value with respect each factor. So the tracing stop at C₁₁ and we need to trace C₁₂, the next sub-class of C₁₁.

C₁₂ is not possible to be divided since the objects in the subclass have same value with respect each factor. So that the tracing stop at C₁₂. It stop the tracing of C₁ and we need to trace C₂, the next sub-class of C₁.

n=9，

f₃=Weight n(1)=9, c_f3=1-(9´8)/9´8=0,

f₁=Sex，n(1)=5, n(2)=4, c_f1=1-(5´4+4´3)/9´8=1-32/72=40/72,

f₂=Weight，n(1)=2, n(2)=6, n(3)=1 c_f2=1-(2´1+6´5+1´0)/9´8=1-32/72=40/72.

     ${c_{{f_1}}} = {c_{{f_2}}}$=maximum. Arbitrarily select one, Sex for example, to do classification. We get that

           ${C_2} = {C_{21}}\{ {u_4}{u_5}{u_6}{u_7}{u_8}\}  + {C_{22}}\{ {u_{13}}{u_{14}}{u_{15}}{u_{16}}\} $

According to the involution, they correspond to three basic concepts ${\beta _{21}} = (MR,{C_{21}}),{\beta _{22}} = (HR,{C_{22}})$. Without statements in detail, we have that

          ${C_{21}} = {C_{221}}\{ {u_4}{u_5}\}  + {C_{212}}\{ {u_6}{u_7}{u_8}\} $

According to the involution, they correspond to three basic concepts ${\beta _{211}} = (MTR,{C_{211}}),{\beta _{22}} = (MAR,{C_{212}})$. ${C_{211}}$ and ${C_{212}}$ are not possible to be divided, and then stop the tracing and go to ${C_{22}}$;

          ${C_{22}} = {C_{221}}\{ {u_{13}}{u_{14}}{u_{15}}\}  + {C_{222}}\{ {u_{16}}\} $

According to the involution, they correspond to three basic concepts ${\beta _{211}} = (MTR,{C_{211}}),{\beta _{212}} = (MAR,{C_{212}}).$. ${C_{221}}$ and ${C_{222}}$ are not possible to be divided, and then stop the tracing and go to ${C_{3}}$;

 

${C_3} = {C_{31}}\{ {u_9}{u_{10}}\}  + {C_{32}}\{ {u_{17}}{u_{18}}{u_{19}}{u_{20}}\} $

According to the involution, they correspond to three basic concepts ${\beta _1} = (ML,{C_{31}}),{\beta _{32}} = (FL,{C_{32}})$. ${C_{31}}$ and ${C_{32}}$ are not possible to be divided, and then tracing is stopped and there is nowhere to go. Stop

4. Drawing the graph

There are 13 basic concepts shown in the graph, including the zero concept ${\beta _0} = (\emptyset ,U)$. There are eight concepts are not to be divided: ${\beta _{11}},{\beta _{12}},{\beta _{21}},{\beta _{23}},{\beta _{31}},{\beta _{221}},{\beta _{222}}$，which are the eight atom concepts mentioned above. The rest 4 non-atom basic concepts are ${\beta _1},{\beta _2},{\beta _3},{\beta _{22}}$.

Like soldiers are lined by battalion, company, platoon, class, the algorithm of index-transposition is very simple, which holds the quickness required by big data.

3.2 Rule extraction

If $R = X({f_1}) \times  \cdots  \times X({f_n})$，then factors ${f_1}, \cdots ,{f_n}$ are called relatively independent. We use the terminoloty to avoid be mixed with independent, which is defined among random variables in probability theory. However, if $R \ne X({f_1}) \times  \cdots  \times X({f_n})$, then there must be influences in between factors ${f_1}, \cdots ,{f_n}$. Factors interact as both cause and effect. If we divide ${f_1}, \cdots ,{f_n}$ into two groups arbitrarily, we can treat the first group factors as condition f and second group as result $g$, then there must be causality from f to $g$. Denoting that $X = X(f),Y = X(g)$, we have had an important theorem as follows:

Given a regular factor space $\psi  = ({\{ X(f)\} _{(f \in F)}};U,X(F))$, where $F = \{ f,g\} $. Let $R$ be the background set with respect to $F$. For any $A \subseteq X(f)$, and set

$${A^*} = \{ y \in X(g)|\exists x \in X(f);(x,y) \in R\} $$(6)

Basic Theorem 1^[16] Theinference $A \to B$ is a tautology (Identically true) if and only if ${A^*} \subseteq B$.

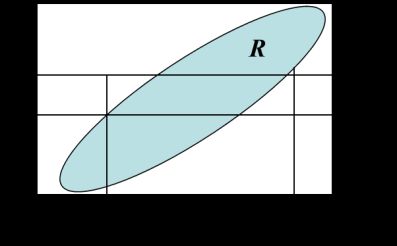Fig 1. Background relation determine tautologies

The theorem declares that background relation determines all tautologies.

How to get tautologies by background relation? There is the second basic algorithm in factor space.

Definition 7^[17], Let $X$ and $Y$ be two qualitative phase spaces, and $s \in X,t \in Y$ be conditional attribute and resulted attribute respectively. For any subset $C$ of the universe $U$, We call $[s] = \{ u \in C|f(u) = s\} $ is a deterministic class of factor $f$ if $[s] \subseteq [t] = \{ u \in C|g(u) = t\} $, The union of deterministic classes of factor $f$ is called the deterministic field, denoted as $D(f)$. Denote that

$$c(f) = |D(f)|/|U|$$ (6)

We call $c(f)$ the deterministic degree of factor on $C$.

Factor Space Algorithm 2^[18] (Causality Analysis)

Given a regular factor space $(U,X(F))$ with $F = ({f_1}, \cdots ,{f_k};g)$, the factorial tableau has tableau-head $(u;{f_1}, \cdots ,{f_k};g)$, extracting tautologies from the tableau.

$C:= U$;

Step 1, For each factor, calculating the deterministic degree on $C$;

Step 2. Selecting a factor $f$ with maximal deterministic degree on $C$. doing index-transposition and getting division on $C$; If $c(f)>0$, then for each deterministic class $[s]$, transferring it as a tautology ${\bf{s}} \to {\bf{t}};U:U\backslash D(f)$.

Step 3 $C:=$ next brother-class if there is one not be transferred; else, $C:=$ next uncle-class if there is one not be transferred;…;Else stop if there is no more subclass not be transferred.

The power of causality: It is the united form of rule-extraction in discrete cases, which is the base of induction.

Modus Ponens(MP): If ${\bf{s}}$ and ${\bf{s}} \to {\bf{t}}$ are tautologies then ${\bf{t}}$ is a tautology.

This is the Boolean logic built on conceptual Boolean algebra.

Let $X(F) = $ be the quantitative or carried qualitative phase space. Given two points in ${x_1} = ({x_{11}}, \cdots ,{x_{1n}}),{x_2} = ({x_{21}}, \cdots ,{x_{2n}})$ in $X$. Since they are two vectors in real or integer space, denote that

$$n({x_1},{x_2}) = \max \{ \min \{ {x_{1j}} - {x_{2j}}\} /{L_j}|j = 1, \cdots ,n\} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({x_1},{x_2} \in X)$$(7)

Where ${L_j}$ is the maximal distance in $X({f_j})$.

Definition 8^[19]Mappingn : ${X^2} \to [0,1]$ is called near degree on $X$.

Factor Space Algorithm 3 ^[20] (Causality inference)

Let $(U,X(F))$ be a regular factor space with $F = ({f_1}, \cdots ,{f_k};g),X = X({f_1}) \times  \cdots  \times X({f_n})$ and $Y=X(g)$. Given${\bf{\tau }} = {\{ {a_i} \to {b_i}\} _{(i = 1, \cdots ,k)}}$,a set of tautologies from $X$ to $Y$, the algorithm performs a approximate inference: Set input as any phase $a \in X$, Output: $y=b$, which is inferred by $x=a$ and ${\bf{\tau }}$.

Step 1, Calculating near degrees $n(a,{a_i}),{a_i}$ is the condition of the $i$-th tautology in ${\bf{\tau }}$,

Step 2. Select $i^*$ such that $n(a,{a_{{i^*}}}) = \max n(a,{a_i})$;

Output: $y = {b_{{i^*}}}$.

 4. Uncertainty in factor space

Thinking process is essentially uncertainty. Factor space theory started from the transformation between certainty and uncertainty. The first author presented the rough idea of factor space when he was teaching probability in 1960s. In this section, we will introduce how to treat uncertainty by factor space theory, and we will introduce how to make factor space theory abundant in handling with uncertainty.

4.1 Randomness in factor space

Throwing a coin, which side will appear? Consider all factors having influences to the throwing process such as the shape of coin; the action of fingers; the character of desk; the environmental influences etc. There is a factor space^[21]. We can set an assumption here: If the considered factors are sufficient enough, then, for any ${\bf{x}} \in X$, the result $\omega  = \omega ({\bf{x}})$ must be face or back. i.e., $\omega$ is a mapping from $X$ to $\Omega  = \{ F,B\} $. If the assumption is not true, then there must be some factors having influence to the result which are not in the consideration. Put them into consideration so that the assumption is true. There comes the consequence: Randomness can be transferred to determination partly whenever the condition factors are more sufficiently in consideration. Randomness occurs due to the lack of the sufficiency of conditional factors' description and measurement.

The world is deterministic and random, which are the dialectically united. We don't think that randomness could be eliminated, but randomness and determinacy are interconvert-able. In the causality space, a subset $C$ is called a condition, which is controlled and identified information towards a random experiment. From a point $x$ to the granule $C$, we only know that $x\in C$ but don't know where it is. If the granule $C$ is enough small such that all points in $C$ correspond to a same result, then it is determinacy; when the granule $C$ is enough big such that $C$ intersects face and back both, in this case, the event occurred may be face or back, it becomes randomness.

Insufficient condition is a condition also, even though it does not determine the occurrence of an event. It determines the occurrence probability of the event. Probability is a generalized causality, which reflects the inner connection between conditional factors and resulted factors.

We can realize the transformation of necessity and randomness by means of factor space. Even though the law of large number and the criterion of Bayesian have been in probability, there is a big room open yet. Factor space treats a random variable as three parts as follows:

$$\xi  = f({\bf{x}}) + \hat f({\bf{x}}) + \delta $$ (8)

Where $f({\bf{x}})$ is a ordinary function caused by deterministic factors，$\hat f({\bf{x}})$ is a fitting function got by sampling, which is caused by random factors. Third term $\delta $ is a random variable with Gaussian distribution caused by big number of factors having weak and independent influences. To decrease randomness, focus on regulating and controlling factors with respect to the middle term in (8).

4.2 Fuzziness in factor spaces

Fuzzy set theory is a great bridge connecting qualitative and quantitative description built by Zadeh L A in 1965^[22].A fuzzy subset is defined as mapping from universe of discussion $U$ to $[0, 1]$, no any statements had been made for $U$. But which is a very important part for the description and controlling of fuzziness. Using factor space to describe $U$, we can make transformation between determinacy and randomness. To score a man on the degree of young, only considering one factor age is not enough. It will be easier if we consider more factors such as face, action, response etc. The key point is: The fuzziness is decreasing while the number of factors is increasing.

Factor space is a common base of fuzzy sets and probability, and we can compare fuzzy sets with probability within factor space. Randomness experiments can be modeled as 'fixed the circle, moving the point', while, fuzziness experiments can be modeled as 'fixed the point, moving the circle'. Such a duality has profound meaning: the circle in $U$ is a point in the power of $U, P(U)$, the point $u$ of $U$ corresponds to $\left\langle u \right\rangle  = \{ A|{\bf{x}} \in A\} $, which is a circle of $P(U)$. A fuzzy phenomena on the ground $U$ can be viewed as a random phenomena in the sky $P(U)$. According to such a duality, fuzzy sets can be described the falling shadow of random sets.. There comes the fuzzy theory based on falling shadow of random sets^[23]，which promotes ordering, topology and measurement structures from universe $U$ to the power $P(U)$, built eight kinds of super-topologies, proved the existence and uniqueness theorems of four subjective non-additive functions. This is a series of deep and rigorous mathematical theorem with new methodology. Most important contribution is moving the start point of measurement extension theorem from semi-ring to $p$–system. Theory pushes practice, the second fuzzy inference machine in the world was successfully developed in 1988, Beijing Normal Univ. The systematical factor space theory on knowledge description was published in 1994^[24] and in 1995^[25].

4.3 Background distribution and fuzzy background relation

Background relations are not deterministic for two reasons: First one, big granule of objects induces randomness. We can say somebody is a student, but we can only say what percentage of student in a family. If we take a family as an object, this is a probabilistic problem; Second one, the qualitative phases are ill defined usually and they are fuzzy sets.

Let $(U,X(F))$ be a qualitative factor space with background relation $R \subseteq X(F),{U^*} = {F^{ - 1}}(R)$. We call $(R,{2^R})$ and $({U^*},{2^{{U^*}}})$ the phase-measurable space and factorial measurable space respectively. For a probability defined on $({U^*},{2^{{U^*}}})$ , we call$({U^*},{2^{{U^*}}}, p )$ a probability field on $U$.

Definition 8^[26]Given a factorial probability field $(R,{2^R},p)$，for any atom intension ${a_{(1) \cdots (n)}}$, denote that ${p_{(1) \cdots (n)}} = p({a_{(1) \cdots (n)}})$，we call P={r_(1)...(n)}the background distribution on $(R,{2^R},p)$.

Set

$$p_i^j = \sum {\{ {p_{(1) \cdots (n)}}|(j) = i\} (i = 1, \cdots ,{c_j})} $$    (8)

$\{ p_i^j|i = 1, \cdots ,{c_j}\} $ is called the marginal distribution of $f_j$，we have that

 $$ p_i^j = \sum {\{ p_i^j|i = 1, \cdots ,{c_j}\} }  = 1$$       

We can define conditional probability:

$$p({b_j}|{a_i}) = p({a_i} \wedge {b_j})/p({a_j})$$                             (9)

Similarly, we can define fuzzy background relation as follows:

Definition 9 ^[26]Let ${\bf{p}} = \{ {p_{(1) \cdots (n)}}\} $ be a background distribution，set $M = \max \{ {p_{(1) \cdots (n)}}|{p_{(1) \cdots (n)}} \in {\bf{p}}\} $，we call that ${\bf{\mu }} = \{ {\mu _{(1) \cdots (n)}}\}  = \{ {p_{(1) \cdots (n)}}/M\} $ is a fuzzy background relation in between ${f_1}, \cdots ,{f_n}$.

Definition 10 ^[24]Given $\lambda  \in [0,1]$，denote that

$${{\bf{\mu }}_\lambda } = \{ {a_{(1) \cdots (n)}} \in X(F)|{\mu _{(1) \cdots (n)}} \ge \lambda \} $$ (10)

Which is called the $\lambda$-background relation of $\mu$.

After background distribution and fuzzy background relation have been introduced, the factor algorithm 3 can be extended to a powerful uncertainty causality inference: It is the united form of inference in discrete cases, which is the base of all rational thinking process: Classification, Judgment, Learning, Predication, Decision Making, Evaluation, Controlling, etc.

 

5 Factor databases

As a base of data science, the main content of factor space is dealing with databases, namely, the factor databases. We will introduce factor databases in the section, which is a network consisting of cognition packets. Each packet is connected with a main factor space, which performs cognition functions to answer variety of problems. Differing from existent data processing, data is the object of cultivation in factor databases and the target of cultivation is approximating background set R by means of its sample S. Once S=R, the packet grasps the whole related correct knowledge. To ensure the powerful function maintains for big data, the background base plays a most important role, which is a compressor without information loss. The network connecting cognition packets is able to evolve to a man-machine cognition system, which has important influence to human being.

5.1 Cognition packets

When the eyes opened firstly at born, baby has only zero-concept, whose intension is empty, and extension is the whole world, a mass of chaos. The human knowledge building is generated from zero-concept step by step. In each step, there is mainly a upper-seat concept a with extension U. Under certain objective, a set F of factors are needed to divide a as a group of sub-concepts with finer intension and smaller extension. In factor databases, there is a cognition packet corresponding to each step, which is a databases organized by a group tableaus. The main tableau of them is a table having a head $({U^*},X(F))$ corresponding to the factor space $(U,X(F))$, where U* is a sample of U. based on the factor space algorithm 1-3, the packets performs a series of algorithms to realize the basic three functions and other functions of thinking process. Those functions provide a consulting service.

Definition 12^[27,28] A cognition packet $K = (\sharp,\psi ,q)$ is defined as a factor space $\psi  = (U,X(F))$ called the main representation space, where U is the extension of a upper-seat concept. The symbol $\sharp$ is asymbol to code the packet in order to connect to other packet; q is a consulting service to answer problems including classification, judgment, learning, predication, decision making, evaluation, controlling, etc.

5.2 Cultivation of data

Background set R is the foundation of knowledge building, which determines concept generation and rule induction and influences all cognition functions. Factor databases get a sample of R in each main tableau. The target of FD is cultivating data such that the population R can be attached.

Definition 13^[27,28] Set that $S = \{ {s_j} = \{ {x_{1i}}, \cdots ,{x_{ni}}\} |i = 1, \cdots ,m\} $，which is called the sample or privacy sample of background set R.

A sample point with respect to the factor tableau with head $({U^*},X(F))$ are an (n+1)-dimensional vector ${\bf{\hat x}} = ({u_j};{x_{1j}}, \cdots ,{x_{ni}})$; while the sample point of R is the n-dimensional sub-vector of ${\bf{\hat x}}$ It cuts out the object u_i from ${\bf{\hat x}}$, that's why do we call it the privacy sample. Adoption of privacy sample avoids the big trouble in big data.

Basic Theorem 2^[28]R=È{S|S is a sample of R}.

The theorem tells us that the population R can be monotonously approximated by the union operation on its samples anywhere. The union operation in sampling is very simple and can be done by distributed computation. Basic theorem 2 inspires the idea of data-cultivation. The generation process of a cognition packet is the approximate process where the cultivated sample S becomes R. S determines the correct cognition rate in related classification or decision making. Apart from the noise carried by data, error rate is essentially determined by the covering rate of S on R. i. e., error occurs whenever the testing point falls down outside S. So，ideally，the error rate can decrease to zero provided S=R.

5.3 Background bases

For quantitative phase spaces, we can define convex background set R, which is held in ordinary cases. For qualitative phase spaces, we can integerize them provided they can be ordered.

Definition 14^[28,29] Let R be a convex background set in a quantitative phase space or a integerized qualitative phase space. Let B be a subset of R. B is called a background base if R is contained by c[B]，the convex hull of B.

Basic Theorem 3 (Inner point judgment Theorem)^[29]. Given a background base B of background set R, x is an inner point of c[B] if and only if

$$\exists {\bf{y}} \in B,({\bf{x}} - \underline {\bf{x}} ,{\bf{y}} - \underline {\bf{x}} ) < 0$$（11）

Where $\underline {\bf{x}}  = \sum {\{ {x_i}|{x_i} \in B\} /|B|}$.

 

Factor space algorithm 4(Base cultivation)^[29]

Given a background base B of R, For a new sample point x of S, real-timely cultivate a new background a new background base B' of R

Step 1. Judging if x is a inner point of c[B], if it is , then B':=B; Else, goto step 2;

Step 2, For each $z \in B$. judging if z is a inner point of $c[B \cup \{ {\bf{x}}\} ]$; If it is , then $B: = B\backslash \{ z\} $;

Output $B': = B \cup \{ {\bf{x}}\} $.

How to get a background base B?

When we meet a sample $S = \{ {x_i} = ({x_{i1}}, \cdots ,{x_{in}})|i = 1, \cdots ,m\} $ of background set R firstly, set

$${B_0} = \{ \inf \{ {x_{ij}}|i = 1, \cdots ,m\} ,\sup \{ {x_{ij}}|i = 1, \cdots ,m\} |j = 1, \cdots ,n\} $$  (12)

B₀ is the rough base we started. Applying algorithm 4 for each sample point of S, we cultivate B₀ to Bwith complexity O(mnk) (m,n,k are the numbers of S,B and factors respectively).The cultivation process real-timely continues to approximating R by c[B], during the recognition network huff 'n' puff big data from internet.

5.4 Man-machine cognition network

Each factor space describes a cognitive cell in knowledge; which is a fork, dividing an upper-seat concept to a group of sub-concepts by means of a group of factors. And each sub-concept can be divided into a group of sub-sub-concept individually again. Liking the spring bud sprouts new leaves, the natural characteristic of factor spaces is tree-image. The connection of factor spaces generates the concept of Factor vine (FV). We omit the definition of factor vine here, but hint that the construction of factor vine can be realized by Wille’s background formal concepts. Instead of the objects-attribute relation tableau, we can get the tree map of factor vine by means of the object-factor relation tableau, which value 1 to a pair $(u, f)$ if the factor $f$ is meaningful for the object $u$. A tree map of a factor vine is a tree of conceptual division: Each node is a name of concept; the only newer point is adding the name of factors aside the node. Without factors, upper-seat concepts cannot be divided into sub-concepts. 

Definition 15^[29,30]  A man-machine cognitive system(MMCS) with respect to a target knowledge  area $K$ is a pair (K,FV), where $K$ is the area of target knowledge, and FV is the factor vine with respect to $K$.

   Even though factor spaces are easily form to factor vine from bottom to up, the MMCS is formed essentially from up to bottom. It is a great engineering. It will change the style of artificial intelligence: From the bottom-top manual work to the combination of top-bottom and bottom-top network; which makes the man-machine cognition network intelligently huff ‘n’ puff big data from internet. MMCSs will be self-organized ecosystems combining man and machine, software and hardware, economy and society. Variety of MMCNs will emerge soon and people cannot imagine what the world will be.

6. Conclusion

As for the existent data science frightened by the multi-challenge of big data, factor space theory brings us a sedative. The tide of big data will be tamed by factor databases. Data is the object of cultivation, no matter how big the tide is, the factor algorithm 4 grasps a little part in the background base real-timely. With the lapse of time, the background base becomes more mature and stable. The cultivation is easy to be made since the sample of background relation don't concern about privacy. The bottlenecks caused by big data can be overcome by factor space theory. Factor space is a best framework for cognition math.

Acknowledge 

 The authors specially thank Professor Yong Shi for his encourage and supports, also thank Professors Hongxing Li, Zengliang Liu, Sicong Guo, Chongfu Huang, Ping He, Qing He, Xiaohong Zhang, Minqiang Gu, and Tiejun Cui for their helps. Thanks for Jun Guo helps the writing of the paper. This study was partially supported by the grants (Grant Nos. 61350003, 11401284, 70621001, 70531040) from the Natural Science Foundation of China.

Reference

[1] Wang P Z. Factor space, a mathematical preparing for the coming of big data tide (special talk), High-end Forum on Big Data, Chinese Academy of Sciences. Beijing, Dec. 2014.

[2] Huang C F. A way to test if wisdom network can improve intelligence(Special talk), International Conference

of Orient Thinking and Fuzzy Logic--The 50th Anniversary of Fuzzy Sets. Dalian, China. Aug. 2015.

[3] zhong Y X，Information Science Principle[M]. Beijing: Beijing University in Posts and Telecommunication Press, 2002.

[4] zhong Y X. Higher Principle of Artificial Intelligence, the Idea, Method, Model and Theory[M]. Beijing: Science Press, 2012

[5] He H C, Ma Y C. Information, Intelligence and Logics[C]. Xi'an: North-west University of Polytechnical Press, 2008

[6] He H C, Wang H, Liu Y H, Wang Y J, Du Y W. Universal Logics Principle[M]. Beijing: Science Press, 2001.

[7] Wille R., Restructuring lattice theory: An approach based on hierarchies of concepts [J]. Ordered Set, 1982: 445-470.

[8] Pawlak Z. Rough sets [J]. International Journal of Computer and Information Sciences, 1982, (11): 341-356.

[9] Wang P Z, Sugeno M. Factor field and the background structure of fuzzy sets[J], Mathematics, 1982 (2): 45-54

[10] Ganter G, Wille R, Formal Concept Analysis[J]. Berlin, Heidelberg: Springer-Verlag, 1999

[11] Wang P Z. Factor space and concept description[J], Journal of Software, 1992. 3(1)：30-40.

[12] Feng J L. Attribute Method in Thinking and Intelligence Science[C]. Beijing: Atomic Energy Press, 1990

[13] Wang P Z. A factor space approach to knowledge representation. Fuzzy Sets and Systems, 1990, (36): 113-124.

[14] Wang P Z, Liu Z L, Shi Y, Guo S C. Factor space, the theoretical base of data science [J]. Ann. Data Science, 2014, 1(2): 233-251.

[15] Wang P Z. Factor space and factorial databasis[J], Journal of Liaoning Technical University(Natural Science), 2013, 32(10): 1-8.

[16]Wang P Z, Zhang X H, Lui H C, Zhang H M, Xu W. Mathematical theory of truth valued inference[J]. Fuzzy Sets and Systems, 1995, 72: 221-238

[17] Wang P Z, Guo S Z, Bao Y K, Liu H T. Causality analysis in factor space[J.] Journal of Liaoning Technical University(Natural Science), , 2015, 34(2): 273-280.

[18] Wang H D, Wang P Z, Shi Y, Liu H T. Improved factorial analysis algorithm in factor spaces[C]. International Conference on Informatics, 2014: 201-204.

[19]Wang P Z, Fuzzy Sets and its Applications[M]. Shanghai: Shanghai Science and Technology Press, 1983.

[20] Liu H T, Guo S Z. Inference model of causality analysis[J]. Journal of Liaoning Technical University(Natural Science), 2015, 34(1): 124-128.

[21] Wang P Z. Randomness//Advance of Statistical Physics, Hao B L,…, Wang P Z(eds), Beijing: Science and Technology Press, 1981

[22] Zadeh L A. Fuzzy sets. Information and Control, 1965,9:388-357.

[23] Wang P Z. Fuzzy Sets and Falling Shadow of Random Sets[M]. Beijing: Beijing Normal University Press, 1985

[24] Wang P Z, Li H X. The Mathematical Theory of Knowledge Representation[M]. Tianjin: Tianjin Science and Technology Press, 1994.

[25] Wang P Z, Li H X. Fuzzy System Theory and Fuzzy Computer[C]. Beijing: Science Press, 1995

[26] Zeng F H, QU G H, Liu Z L, Wang P Z. Background distribution and fuzzy background relation[J]. Fuzzy Systems and Mathematics (Accepted)

[27] Wang P Z, Factor space and data science[J]. Journal of Liaoning Technical University(Natural Science), 2015, 34(2): 273-280.

[28] Liu H T. Liu Z L, He H C, He P. Overview of the development of factor space[J]. Fuzzy Systems and Mathematics (Accepted)

[29] Wang P Z etc, Background bases, (Working paper)

[30] Liu Z L, Theory of Factorial Neural Networks[M]. Beijing: Beijing Normal University, 1990.

 

This paper will be published on Annals of Data Science, Springer. You can download it from: http://pan.baidu.com/disk/home#list/path=%2F

 If you have any problems about this paper, please contact [email protected].

 

转载于:https://www.cnblogs.com/huadongw/p/5614154.html