【机器学习】决策树

目录

1、决策树概念

2、ID3、C4.5、CART的区别

2.1、ID3算法：只能处理离散型的数据

2.2、C4.5算法

2.3、CART算法（Classification And Regression Tree）：分类回归树

3、总结

4、模型调参注意事项

5、决策树生成

6、决策树剪枝

---

1、决策树概念

决策树也称为分类树（分类）或者回归树（数值预测）。是一种有监督的机器学习算法，是一个分类算法。在给定训练集的条件下，生成一个自顶而下的决策树，树的根为起点，树的叶子为样本的分类，从根到叶子的路径就是一个样本进行分类的过程。

决策树：是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。决策树优点：1）模型容易展示：决策树模型可读性好，具有描述性，有助于人工分析；2）效率高，决策树只需要一次构建，反复使用。3）训练时间复杂度较低，预测的过程比较快速，每一次预测的最大计算次数不超过决策树的深度

2、ID3、C4.5、CART的区别

2.1、ID3算法：只能处理离散型的数据

ID3算法用于决策树建立的过程： 
（1）对于当前的所有样本集合，计算每个属性的信息增益（即划分前后数据集的熵的差异） 
（2）选择信息增益最大的属性（假设为Ai） 
（3）把在Ai处取值相同的样本归于同一个子集，Ai有几个属性，就合成几个子集 
（4）重复以上的三个过程，直到结束（熵值为0或者一个阈值） 
ID3算法使用的是自顶向下的贪婪搜索遍历可能的决策树空间构造，属于局部最优，不一定全局最优。

停止条件为： 
1）该节点的所有样本属于同一类，该节点成为叶节点，存放相应的类别。 
2）所有的属性都已被父节点或祖先使用。这种情况下，该节点成为叶节点，并以样本中元组个数最多的类别作为类别标记，同时也可以存放该结点样本的类别分布。

ID3缺点： 
1）容易造成过度拟合（over fitting）； 
2）只能处理离散型数据； 
3）信息增益的计算依赖于特征数目较多的特征，而属性取值最多的属性并不一定最优； 
4）抗噪性差，训练例子中正例和反例的比例较难控制

2.2、C4.5算法

可以处理连续型和离散型的数据，处理连续型的数据时和CART的回归树处理方法类似 

C4.5是另一种决策树构造算法，它是上文ID3的一个改进。主要的差别如下： 
（1）用信息增益率代替信息增益来选择属性，ID3选择属性用的是子树的信息增益，而C4.5用的是信息增益率。克服了用信息增益选择属性时偏向选择取值多的属性的不足。 
（2）在树构造过程中进行剪枝。合并相邻的无法产生大量信息增益的叶节点，消除过渡匹配问题。 
（3）既能处理离散型数据，又能连续型数据。为了处理连续型数据，该算法在相应的节点使用一个属性的阈值，利用阈值将样本划分成两部分。 
（4）能处理缺失了一些属性的数据。该算法允许属性值缺失时被标记为？，属性值缺失的样本在计算熵增益时被忽略。 

C4.5的优点：产生的分类规则易于理解，准确率较高。 
C4.5的缺点： 
1：算法低效，在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效 
2：内存受限，只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。 
另外，无论是ID3还是C4.5最好在小数据集上使用，决策树分类一般只适用于小数据。当属性取值很多时最好选择C4.5算法，ID3得出的效果会非常差。

2.3、CART算法（Classification And Regression Tree）：分类回归树

选择那个使得划分后基尼指数最小的属性作为最优划分属性。

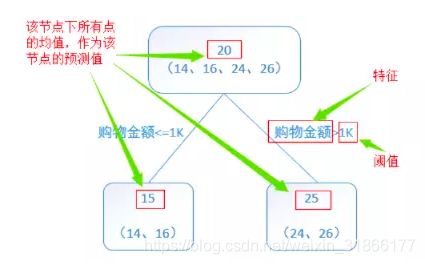
CART既可以用于分类也可以用于回归，回归树其实并没有使用线性回归，而是使用到达叶子节点的样本的均值。CART模型既可以用于分类、也可以用于回归，对于回归树（最小二乘回归树生成算法），需要寻找最优切分变量和最优切分点，对于分类树（CART生成算法），使用基尼指数选择最优特征。 

CART也是决策树的一种生成算法，主要的差别在于CART的决策是二叉树的，它同样可以处理离散值，但是，只能选择其中一种来把数据分成两个部分。 

CART与ID3区别：ID3和CART算法的区别主要集中在树的生成和树的修剪方面，但是ID3算法只能处理离散型的属性 
1）CART中用于选择属性的不纯性度量是Gini指数； 
2）如果目标变量是离散的，并且是具有两个以上的类别，则CART可能考虑将目标类别合并成两个超类别（双化）； 
3）如果目标变量是连续的，则CART算法找出一组基于树的回归方程来预测目标变量。

回归树的缺点：不如线性回归普遍；要求大量训练数据；难以确定某个特征的整体影响；比线性回归模型难解释

基尼不纯度是一种度量集合有多纯的方法，如果集合里面的值都是一个数的话，则基尼不纯度的值为0，随着混合的东西越多，则基尼不纯度值越高。 

“熵”是对混乱程度的度量，越乱熵越大，与之相对应的概念是“序”，就是有规律。越有序，越纯，熵越小；越乱，熵越大，越不纯。

3、总结

总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似），最好的划分就是使得GINI_Gain最小的划分。 

• 1、 决策树度量方式的选择

1） 信息增益：倾向多值属性； 
2） 增益率：倾向不平衡分裂，其中一个子集比其它小很多； 
3） Gini index：偏向多值属性；当类数目较大时，计算困难；倾向导致大小相等的分区和纯度。 

• 2、决策树解决过度拟合 

过度拟合：也就是该决策树对训练数据可以得到很低的错误率，但是运用到测试数据上却得到非常高的错误率。过渡拟合的原因有以下几点： 
①噪音数据：训练数据中存在噪音数据，决策树的某些节点有噪音数据作为分割标准，导致决策树无法代表真实数据。 
②缺少代表性数据：训练数据没有包含所有具有代表性的数据，导致某一类数据无法很好的匹配，这一点可以通过观察混淆矩阵（Confusion Matrix）分析得出。 
③多重比较（Mulitple Comparition）：举个列子，股票分析师预测股票涨或跌。假设分析师都是靠随机猜测，也就是他们正确的概率是0.5。每一个人预测10次，那么预测正确的次数在8次或8次以上的概率为 0.0547，只有5%左右，比较低。但是如果50个分析师，每个人预测10次，选择至少一个人得到8次或以上的人作为代表，那么概率为 0.9399，概率十分大，随着分析师人数的增加，概率无限接近1。但是，选出来的分析师其实是打酱油的，他对未来的预测不能做任何保证。上面这个例子就是多重比较。这一情况和决策树选取分割点类似，需要在每个变量的每一个值中选取一个作为分割的代表，所以选出一个噪音分割标准的概率是很大的。

• 优化方案1：修剪枝叶 

决策树过渡拟合往往是因为节点过多，所以需要裁剪（Prune Tree）枝叶。裁剪枝叶的策略对决策树正确率的影响很大。主要有两种裁剪策略： 
①先剪枝：在构建决策树的过程时，提前停止。那么，会将切分节点的条件设置的很苛刻，导致决策树很短小。结果就是决策树无法达到最优。实践证明这中策略无法得到较好的结果。 
②后剪枝：决策树构建好后，然后才开始裁剪。采用两种方法：1）用单一叶节点代替整个子树，叶节点的分类采用子树中最主要的分类；2）将一个子树完全替代另外一颗子树。后置裁剪有个问题就是计算效率，有些节点计算后就被裁剪了，导致有点浪费。

• 优化方案2：K-Fold Cross Validation 

首先计算出整体的决策树T，叶节点个数记作N，设i属于[1,N]。对每个i，使用K-Fold Validataion方法计算决策树，并裁剪到i个节点，计算错误率，最后求出平均错误率。这样可以用具有最小错误率对应的i作为最终决策树的大小，对原始决策树进行裁剪，得到最优决策树。

• 优化方案3：Random Forest

Random Forest是用训练数据随机的计算出许多决策树，形成了一个森林。然后用这个森林对未知数据进行预测，选取投票最多的分类。实践证明，此算法的错误率得到了进一步的降低。这种方法背后的原理可以用“三个臭皮匠定一个诸葛亮”这句谚语来概括。一颗树预测正确的概率可能不高，但是集体预测正确的概率却很高。 

4、模型调参注意事项

• 当样本少数量但是样本特征非常多的时候，决策树很容易过拟合，一般来说，样本数比特征数多一些会比较容易建立健壮的模型
• 如果样本数量少但是样本特征非常多，在拟合决策树模型前，推荐先做维度规约，比如主成分分析（PCA），特征选择（Losso）或者独立成分分析（ICA）。这样特征的维度会大大减小。再来拟合决策树模型效果会好。
• 推荐多用决策树的可视化，同时先限制决策树的深度（比如最多3层），这样可以先观察下生成的决策树里数据的初步拟合情况，然后再决定是否要增加深度。
• 在训练模型先，注意观察样本的类别情况（主要指分类树），如果类别分布非常不均匀，就要考虑用class_weight来限制模型过于偏向样本多的类别。
• 决策树的数组使用的是numpy的float32类型，如果训练数据不是这样的格式，算法会先做copy再运行。
• 如果输入的样本矩阵是稀疏的，推荐在拟合前调用csc_matrix稀疏化，在预测前调用csr_matrix稀疏化。

5、决策树生成

ID3算法
ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地建构决策树。

其具体方法为：从根结点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。ID3相当于用极大似然法进行概率模型的选择。但是ID3算法只有树的生成，所以该算法生成的树容易产生过拟合。

C4.5
与ID3算法相似，C4.5算法对ID3算法进行了改进，C4.5在生成的过程中，用信息增益比来选择特征

CART
分类树与回归树（classification and regression tree，CART）模型（Breiman）由特征选择、树生成及剪枝组成，既可用于分类也可用于回归。CART是在给定输入随机变量X条件下输出变量Y的条件概率分布的学习方法。它假定决策树是二叉树，内部取值为“是”（左分支）和“否”（右分支）。

它的基本步骤为：

1）决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大。
2）决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这是用损失函数最小作为剪枝的标准。

对分类树用基尼系数（Gini index）最小化准则，进行特征选择，生成二叉树，其具体步骤如下：

接下来具体说说回归树是如何进行特征选择生成二叉回归树的。

我们可以通过下面的图来具体的体会回归树的生成过程：

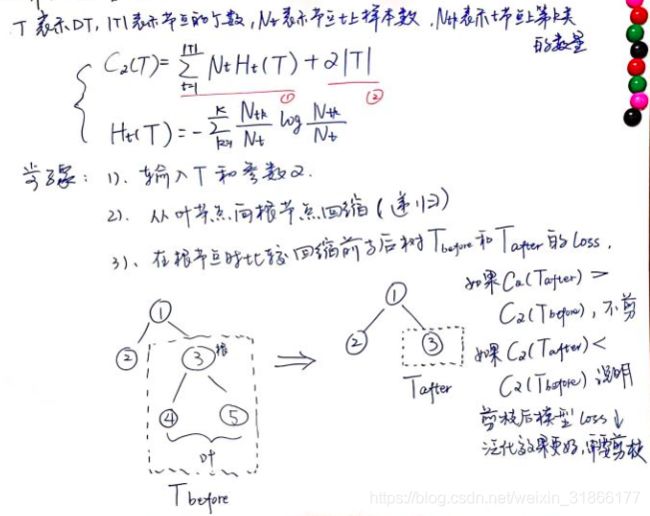
6、决策树剪枝

      决策树的过拟合指的是学习时过多地考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树。解决过拟合的办法是考虑决策树的复杂度，对已生成的决策树进行简化，即剪枝（从已生成的树上裁剪调一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化分类树模型）。

下图展示了决策树剪枝的过程：

emmm

---

问题：cart只能是二叉树吗？也可以是多叉。

---

参考：

复习：决策树@山隹木又

2、决策树ID3、C4.5、CART

决策树调参说明（DecisionTreeClassifier）

决策树之 CART

决策树@文哥的学习日记

决策树算法原理(上)

决策树算法原理(下)