聚类算法

一、K-means算法
K-means是最常用的聚类算法。它的主要思想为:定义几个聚类中心，根据所有数据中所有点到聚类中心的距离，将数据集中的点分配给聚类中心。属于一个聚类中心的所有点就属于一个簇。接着根据分配给聚类中心的点产生新的聚类中心。接着重复以上步骤，直至收敛(即聚类结果不再改变或者达到规定的迭代次数)。实际上，K-means算法是一种EM算法：E步,将数据分配给聚类中心；M步，产生新的聚类中心。
那么如何在每一步迭代中产生新的聚类中心？考虑给定样本集$D=\{{\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_{\mathbf{m}}\}$,假设聚类所得划分为$C=\{C_1,C_2,...,C_k\}$,对应的聚类中心为$\{{\mathbf{\mu }}_1,{\mathbf{\mu }}_2,...,{\mathbf{\mu }}_{\mathbf{k}}\}$,我们一定希望聚类中的数据距离对应聚类中心的距离很小，于是我们可以定义一个最小平方误差，我们只要最小化这个误差即可：
$$E=\sum _{i=1}^k\sum _{x\in C_i}|\mathbf{x}-{\mathbf{\mu }}_{\mathbf{i}}{|}^2$$
里面的求和符号表示对属于簇$C_i$的所有数据的误差求和。外面的求和符号表示对所有簇的误差求和。由于我们每一次迭代都需要求求得聚类中心，所有我们对$E$求导，解得最优聚类中心${\mathbf{\mu }}_{\mathbf{i}}$:
$$\frac{\partial E}{\partial {\mu }_i}=2\sum _{i=1}^k\sum _{x\in C_i}(\mathbf{x}-{\mathbf{\mu }}_{\mathbf{i}})=0$$,明显对于特定的聚类中心${\mathbf{\mu }}_{\mathbf{i}}$
$$\sum _{x\in C_i}(\mathbf{x}-{\mathbf{\mu }}_{\mathbf{i}})=0$$,即：
$${\mathbf{\mu }}_{\mathbf{i}}=\frac{1}{|C_i|}\sum _{x\in C_i}\mathbf{x}$$。即每一次迭代的聚类中心为上一轮对应聚类中的数据平均。
算法步骤:
1、初始化k个聚类中心，k为我们想要将数据划分为几个簇的簇数。一般这些聚类中心是随机产生，或者利用一些算法挑选(如K-Means++)
2、将数据划分到最近的聚类中心。一般这里所使用的距离度量为欧几里得距离或者余弦距离。
3、将聚类中心更新为对应簇内的点的平均。
4、重复2，3步直至聚类中心不在改变或者到达预定的迭代次数。

下面为K-means算法的代码:

def kmeans(X,num_cluster,num_iter=100):
   num_points,dim=X.shape
   initial_rank = np.random.choice(num_points,size=num_cluster,replace=False)
   centers = X[initial_rank]
   assignments = np.zeros(num_points)
   for i in range(num_iter):
       assignments_new=np.zeros(num_points)
       for j in range(num_points):
           min_dist = 100000000000000
           point = X[j]
           for k in range(num_cluster):
               dist = np.sqrt(np.sum((point-centers[k])**2))
               if dist<min_dist:
                   min_dist=dist
                   min_rank = k
           assignments_new[j]=min_rank
       if (assignments == assignments_new).all():
            break
       else:
            assignments = assignments_new
       for n in range(num_cluster):
            centers[n] = np.mean(X[np.where(assignments==n)[0]],axis=0)
   return assignments

这里num_cluster为设定的聚类簇数；num_iter为最大迭代次数，如果到达最大迭代次数聚类结果依然改变，就停止迭代。如果在num_iter之前聚类结果就不改变，就提前停止。输出为一个大小为数据量的数组，其中每一个元素对应聚类的簇编号。
下面看看其聚类结果，我们创建4个满足正态分布的簇,查看结果:

# Cluster 1
mean1 = [-1, 0]
cov1 = [[0.1, 0], [0, 0.1]]
X1 = np.random.multivariate_normal(mean1, cov1, 100)

# Cluster 2
mean2 = [0, 1]
cov2 = [[0.1, 0], [0, 0.1]]
X2 = np.random.multivariate_normal(mean2, cov2, 100)

# Cluster 3
mean3 = [1, 0]
cov3 = [[0.1, 0], [0, 0.1]]
X3 = np.random.multivariate_normal(mean3, cov3, 100)

# Cluster 4
mean4 = [0, -1]
cov4 = [[0.1, 0], [0, 0.1]]
X4 = np.random.multivariate_normal(mean4, cov4, 100)

# Merge two sets of data points
X = np.concatenate((X1, X2, X3, X4))

# Plot data points
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal')
plt.show()

from segmetation import kmeans
assignments = kmeans(X, 4)
for i in range(4):
    cluster_i = X[assignments==i]
    plt.scatter(cluster_i[:, 0], cluster_i[:, 1])

plt.axis('equal')
plt.show()

得到:


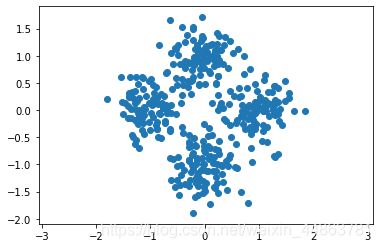
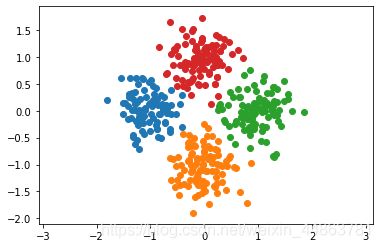
但是实际上上面的代码具有太多for循环，可能导致程序代价过高，下面为改进：

def kmeans_fast(X,num_cluster,num_iter=100):
    num_points,dim = X.shape
    initial_rank = np.random.choice(num_points,size=num_cluster,replace=False)
    centers = X[initial_rank]
    assignments=np.zeros(num_points)
    for i in range(num_iter):
        distance_mat = cdist(X,centers)
        assignments_new = np.argmin(distance_mat,axis=1)
        if (assignments == assignments_new).all():
            break
        else:
            assignments = assignments_new
        for j in range(num_cluster):
            centers[j] = np.mean(X[np.where(assignments==j)[0]],axis=0)
    return assignments

对相同数据，采用kmeans_fast

from segmetation import kmeans_fast
assignments = kmeans_fast(X, 4)
for i in range(4):
    cluster_i = X[assignments==i]
    plt.scatter(cluster_i[:, 0], cluster_i[:, 1])
plt.axis('equal')
plt.show()

输出:

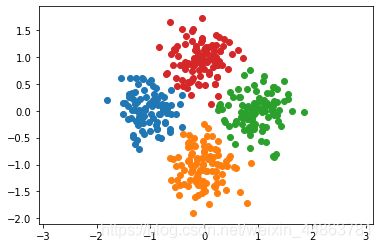
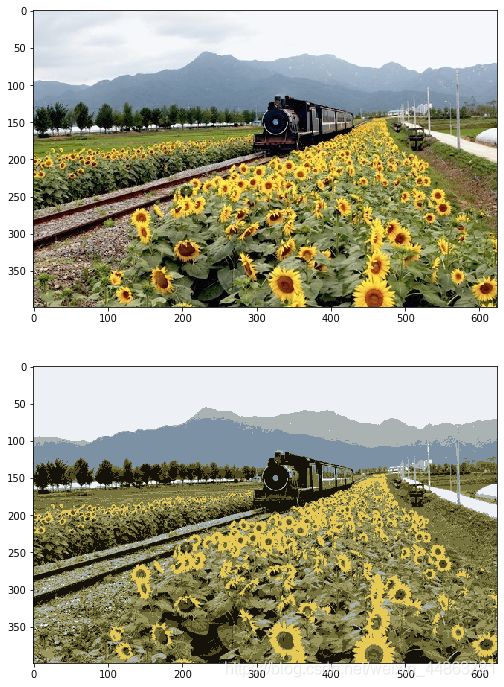
下面我们将这个算法应用到图片中：将图片中的像素进行聚类,而像素的特征为RGB亮度三个数值，然后将像素替换为对应的聚类中心，首先为将图片中像素替换为聚类中心的函数和图片转化为特征的函数:

def visualize_mean_color_image(image, assignment):
    H,W,C = image.shape
    k = np.max(assignment)+1
    output = np.zeros((H,W,C))
    for i in range(k+1):
        mean_pixel = np.mean(image[assignment==i],axis=0)
        output[assignment==i] = mean_pixel
    output = output.astype(int)
    return output

def color_feature(image):
    H,W,C = image.shape
    image_float = img_as_float(image)
    feature = image_float.reshape((H*W,C))
    mean = np.mean(feature,axis=0).reshape((1,C))
    std = np.std(feature,axis=0).reshape((1,C))
    feature = (feature - mean) / std
    return feature

接下来查看输出图片：

from segmetation import color_feature,visualize_mean_color_image
image = io.imread('train.jpg')
H,W,C = image.shape
feature = color_feature(image)
assignments = kmeans_fast(feature,8)
assignments = assignments.reshape((H,W))
output = visualize_mean_color_image(image, assignments)
plt.figure(figsize=(15,12))
plt.subplot(211)
plt.imshow(image)
plt.subplot(212)
plt.imshow(output)
plt.show()

得到

二、层次聚类
层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用"自底向上"的聚类策略，也可采用“自顶向下”的分拆策略。
AGNES是一种采用自底向上的聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。而关于聚类簇之间的距离如何计算，有以下几种方法:
1、Single link：$$d(C_i,C_j)=mi{n}_{x\in C_i,x^{{}^{\prime }}\in C_j}d(x,x^{{}^{\prime }})$$
2、Complete link:$$d(C_i,C_j)=ma{x}_{x\in C_i,x^{{}^{\prime }}\in C_j}d(x,x^{{}^{\prime }})$$
3、Average link:$$d(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum _{x\in C_i,x^{{}^{\prime }}\in C_j}d(x,x^{{}^{\prime }})$$

算法步骤如下：
1、初始化每个点作为一个簇
2、找到距离最近的簇
3、将距离最近的两个簇合并
4、重复2,3，直至到达指定的簇数。

代码如下:

import numpy as np
import matplotlib.pyplot as plt

class AGNES:
    def __init__(self,k,X):
        self.k = k
        self.X = X
        self.m = X.shape[0]
        
    def caculate_distanceC(self,C_1,C_2):
        n_1=len(C_1)
        n_2=len(C_2)
        sum_d=0
        for i in range(n_1):
            for j in range(n_2):
                d = self.distance(C_1[i],C_2[j])
                sum_d += d
        return sum_d/(n_1*n_2)
    
    def distance(self,x1,x2):
        return np.sqrt(np.sum((x1-x2)**2))
    
    def caculate_M(self):
        M = np.zeros((self.m,self.m))
        for i in range(self.m-1):
            for j in range(i+1,self.m):
                M[i,j]=self.distance(self.X[i,],self.X[j,])
                M[j,i]=M[i,j]
        return M
    
    def find_min_d(self,M):
        m = M.shape[0]
        min_d = 100000000000
        new_i=0
        new_j=0
        for i in range(m-1):
            for j in range(i+1,m):
                if min_d>M[i,j]:
                    new_i = i
                    new_j = j
                    min_d = M[i,j]
        return new_i,new_j

    def init_cluster(self):
        init_cluster = []
        init_assignments = []
        for i in range(self.m):
            init_cluster.append([self.X[i,:]])
            init_assignments.append([i])
        return init_cluster,init_assignments
    
    def cluster(self):
        q = self.m
        M=self.caculate_M()
        cluster_list,assignments=self.init_cluster()
        while q>self.k:
            i,j=self.find_min_d(M)
            list_i=cluster_list[i]
            list_j=cluster_list[j]
            cluster_list[i]=list_i+list_j
            assignments[i] = assignments[i]+assignments[j]
            del cluster_list[j]
            del assignments[j]
            M = np.delete(M,j,axis=0)
            M = np.delete(M,j,axis=1)
            for t in range(q-1):
                M[t,i]=self.caculate_distanceC(cluster_list[i],cluster_list[t])
                M[i,t]=M[t,i]
            q=q-1
        assignments_array=np.zeros(self.m)
        for i in range(self.k):
            for element in assignments[i]:
                assignments_array[element]=i
        return assignments_array

其中算法中方阵M的第i行第j列为簇$C_i$和$C_j$的距离。查看聚类效果：

# Cluster 1
mean1 = [-1, 0]
cov1 = [[0.1, 0], [0, 0.1]]
X1 = np.random.multivariate_normal(mean1, cov1, 100)

# Cluster 2
mean2 = [0, 1]
cov2 = [[0.1, 0], [0, 0.1]]
X2 = np.random.multivariate_normal(mean2, cov2, 100)

# Cluster 3
mean3 = [1, 0]
cov3 = [[0.1, 0], [0, 0.1]]
X3 = np.random.multivariate_normal(mean3, cov3, 100)

# Cluster 4
mean4 = [0, -1]
cov4 = [[0.1, 0], [0, 0.1]]
X4 = np.random.multivariate_normal(mean4, cov4, 100)

# Merge two sets of data points
X = np.concatenate((X1, X2, X3, X4))

cluster_ = AGNES(4,X)
assignments=cluster_.cluster()

for i in range(4):
    cluster_i = X[assignments==i]
    plt.scatter(cluster_i[:, 0], cluster_i[:, 1])

plt.axis('equal')
plt.show()

输出为：

三、聚类算法分割图像前景和背景
这里我们利用聚类分割前景和背景的想法是：将图像中每个像素作为一个数据，组成数据集，然后定义聚类的簇数k，每个簇的中点作为前景，其他簇的点作为背景。
这里我们首先定义三中特征表示，一种是只含有亮度信息；第二种既含有亮度信息，有含有位置信息；第三种含有亮度信息，位置信息，和两个方向梯度的大小；第四种含有亮度信息，位置信息和梯度方向。这几个特征表示函数分别为：

def color_feature(image):
    H,W,C = image.shape
    image_float = img_as_float(image)
    feature = image_float.reshape((H*W,C))
    mean = np.mean(feature,axis=0).reshape((1,C))
    std = np.std(feature,axis=0).reshape((1,C))
    feature = (feature - mean) / std
    return feature

def color_position_feature(image):
    H,W,C = image.shape
    image_float = img_as_float(image)
    feature = np.zeros((H*W,C+2))
    for i in range(H):
        for j in range(W):
            index = i*W + j
            feature[index,:C] = image_float[i,j]
            feature[index,C] = i
            feature[index,C+1] = j
    mean = np.mean(feature,axis=0).reshape((1,C+2))
    std = np.std(feature,axis=0).reshape((1,C+2))
    feature = (feature - mean) / std
    return feature

def my_features(image):
    H,W,C = image.shape
    image_float=img_as_float(image)
    image_grey = skimage.color.rgb2grey(image_float)
    Gx,Gy = np.gradient(image_grey)
    feature = np.zeros((H*W,C+4))
    for i in range(H):
        for j in range(W):
            index = i*W + j
            feature[index,:C] = image_float[i,j]
            feature[index,C] = i
            feature[index,C+1] = j
            feature[index,C+2] = Gx[i,j]
            feature[index,C+3] = Gy[i,j]
    mean = np.mean(feature,axis=0).reshape((1,C+4))
    std = np.std(feature,axis=0).reshape((1,C+4))
    feature = (feature - mean) / std
    return feature

def my_features1(image):
    H,W,C = image.shape
    image_float=img_as_float(image)
    image_grey = skimage.color.rgb2grey(image_float)
    Gx,Gy = np.gradient(image_grey)
    theta = np.arctan2(Gy,Gx)
    feature = np.zeros((H*W,C+3))
    for i in range(H):
        for j in range(W):
            index = i*W + j
            feature[index,:C] = image_float[i,j]
            feature[index,C] = i
            feature[index,C+1] = j
            feature[index,C+2] = theta[i,j]
    mean = np.mean(feature,axis=0).reshape((1,C+3))
    std = np.std(feature,axis=0).reshape((1,C+3))
    feature = (feature - mean) / std
    return feature

下面为找到最佳的k和特征组合的函数:

def compute_accuracy(mask_gt,mask):
    accuracy_matrix = (mask_gt==mask).astype(int)
    H,W = accuracy_matrix.shape
    accuracy = np.sum(accuracy_matrix) / (H*W)
    return accuracy

def evaluate_segments(mask_gt,segments):
    num_segments = int(np.max(segments) + 1)
    max_accuracy = 0
    for i in range(num_segments):
        mask = (segments==i).astype(int)
        accuracy = compute_accuracy(mask_gt,mask)
        if accuracy>max_accuracy:
            max_accuracy = accuracy
            max_i = i
    return max_accuracy,max_i

def select(image,k,feature_func=0):
    if feature_func==0:
        feature = color_feature(image)
    elif feature_func==1:
        feature = color_position_feature(image)
    elif feature_func==2:
        feature = my_features(image)
    else feature_func==3:
        feature = my_features1(image)
    assignments = kmeans_fast(feature,k)
    H,W,C = image.shape
    segments = assignments.reshape((H,W))
    return segments.astype(int)

这里的第一个函数为根据聚类得到的前景分割情况和Ground Truth一幅图像精确率。第二个函数分别将不同簇中的点作为前景，得到精确率最高的簇和对应精确率。第三个函数则是输入不同的聚类簇数k和特征表示，得到分割图像。

from os import listdir
image_path='./imgs'
gt_path = './gt'
image_list = listdir(image_path)
gt_list = listdir(gt_path)

max_mean_accuracy = 0
accuracy_mean = 0
for i in range(4):
    for k in range(2,6):
        for image_name in image_list:
            image = io.imread('imgs/'+image_name)
            gt = io.imread('gt/'+image_name[:-4]+'.png')
            gt = (gt!=0).astype(int)
            segments = select(image,k,feature_func=i)
            accuracy,i = evaluate_segments(gt,segments)
            accuracy_mean = accuracy_mean + accuracy
        accuracy_mean = accuracy_mean / len(image_list)
        if accuracy_mean>max_mean_accuracy:
            best_k = k
            best_i = i
            max_mean_accuracy = accuracy_mean

print(best_k,best_i,accuracy_mean)

得到

4 1 0.8288612885885763

即聚类簇数选为4，选用第二种特征表示效果最好。现在我们拿出几幅图像看看效果：

for i in range(5):
    image = io.imread('imgs/'+image_list[i])
    gt = io.imread('gt/'+image_list[i][:-4]+'.png')
    gt = (gt!=0).astype(int)
    segments = select(image,4,1)
    accuracy,k = evaluate_segments(gt,segments)
    segments = (segments==k).astype(int)
    plt.figure(figsize=(15,12))
    plt.subplot(311)
    plt.imshow(image)
    plt.subplot(312)
    plt.imshow(segments)
    plt.subplot(313)
    plt.imshow(gt)
    plt.show()

得到

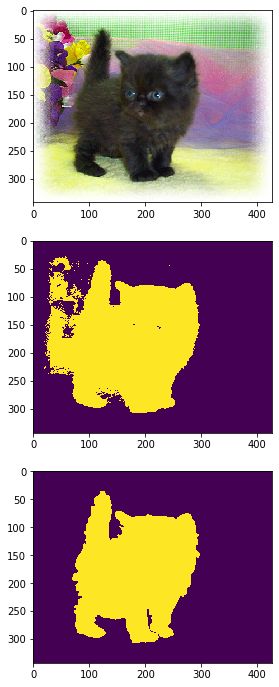
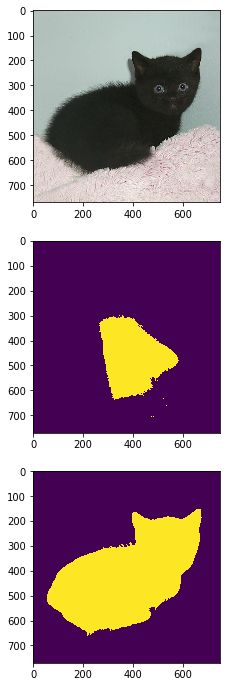
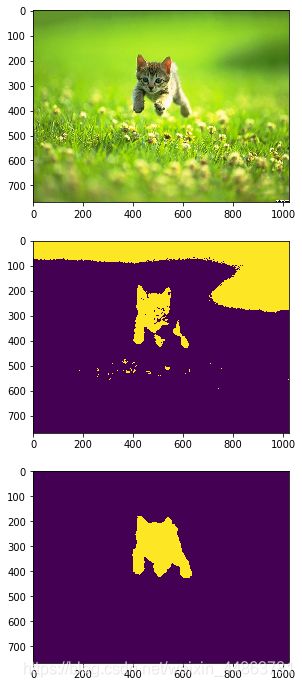
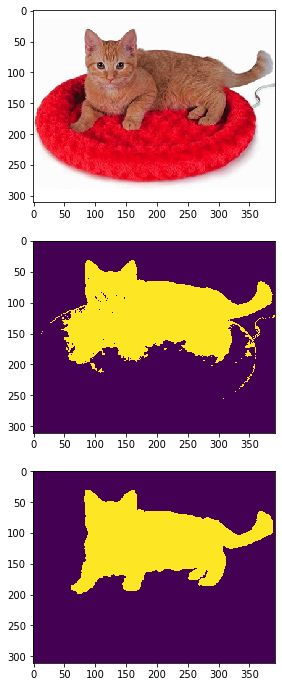
实际上效果并不好，主要是:1、k的不确定，不如这里我们的k=4，但是加入一幅图像有一个黑色的前景，白色的背景，则这里实际上k=4则聚类簇数过多；2、这种方法无法辨别前景物体中的颜色变化；3、前景可能和背景拥有相似的颜色或者说特征。