分组卷积和空洞卷积总结

参考链接：分组卷积(Group conv)与深度可分离卷积(Depthwise separable conv) - 知乎

【深度学习】空洞卷积（Atrous Convolution）_行者无疆兮的博客-CSDN博客_空洞卷积 

一、分组卷积

1.卷积核参数计算量：

k1*k2*c1*c2 (k1,k2为卷积核大小，c1为inchannels，c2为outchannels)

        正常卷积计算：首先卷积核的深度肯定和输入一样为C1，卷积过程是对应输入卷一次(加权求和)得一个值，最终一个卷积核卷出一层的特征图，此时的参数量（为什么不考虑输入的参数量呢，因为网络更新是更新的卷积核啊）为h1*w1*c1,这是一个卷积的参数，对应输出的通道为c2，需要c2个卷积核，因此总参数量为:h1*w1*c1*c2。

2.分组卷积的概念和参数量计算

①概念：分组卷积,即ResNeXt,是受到Inception和AlexNet的启发。Inception的论文中提到,对于卷积来说,卷积核可以看做一个三维的滤波器:通道维+空间维,常规的卷积操作其实就是实现通道相关性和空间相关性的联合映射。Inception 模块的背后存在这样的一种假设:卷积层通道间的相关性和空间相关性是可以退耦合的,将它们分开映射,能达到更好的效果.具体来说,经过不同卷积路径得到的特征图之间的耦合性较低,关注的主要特征不同,可以得到互为补充的特征图,以更完整的表示图像。

②参数计算：如图设分为g个组，g要能被c1,c2整除，因为卷多少分之一输入，生成的特征图个数也为原本的多少分之一。那么，卷积核深度为c1/g,同时负责卷积输入的c1/g个通道，同时卷积核个数也为c2/g。因为卷积后的特征图的数量(channel)为c2/g,计算量为：k1*k2*c1/g * c2/g。一共分了g个组，总参数量为：k1*k2*c1/g c2/g g = k1*k1*c1*c2/g ，比正常的卷积要少了g分之一的参数量。

③代码实现：

import torch
import torch.nn as nn
...
model = nn.Conv2d(in_channels = in_channel, out_channels = out_channel, 
kernel_size = kernel_size, stride = stride, padding = 1, dilation = dilation, group = group_num)

3.深度可分离卷积的概率和参数量计算

 

①概念：是分组卷积的一个极端情况，将组数设置为输入通道数，即每一个输入通道都由一个专门的卷积核负责卷积。但是要经过两个操作，分别是：depth_wise和point_wise卷积，depth_wise和分组卷积一样得到了c1深度的特征图，然后再通过1*1*c2的卷积核调整通道数。（思考：convnext的实现中没有pointwise的原因：输入和输出通道数相同，因此无需调整，那如果c2能够整除c1呢，不能直接在第一阶段生成c2/c1个特征图吗，然后在组合起来？？）

②参数量计算：depth_wise阶段，卷积核的大小是k1 * k2 * 1,分别卷积输入中的一个通道，得到特征图一张, 使用了c1个卷积核，最终特征图为c1个，这里计算量为:k1*k2*1*c1 ，然后就是point_wise, 卷积核大小1*1 
*c1 ,一共c2个，计算量为：1*1*c1*c2，总计算量：k1*k2*c1 + c1*c2

③代码：

import torch
import torch.nn as nn
...
model = nn.Sequential(
        nn.Conv2d(in_channels = in_channel, out_channels = in_channel, 
kernel_size = kernel_size, stride = stride, padding = 1, dilation = dilation, group = in_channel),
        nn.Conv2d(in_channels = in_channel, out_channels = out_channel kernel_size = 1, padding = 0)
        )

二、空洞卷积（膨胀卷积）

 

 

 

1.概念

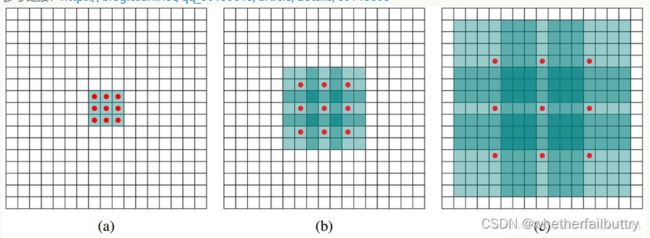
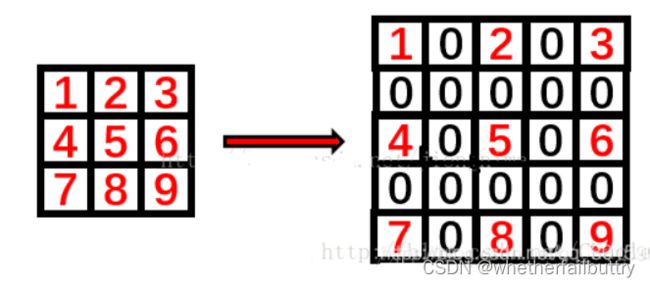
        空洞卷积是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野，让原本3x3的卷积核，在相同参数量和计算量下拥有5x5或者更大的感受野，从而无需下采样。向卷积层引入了一个称为“扩张率(dilationrate)”的新参数，该参数定义了卷积核处理数据时各值的间距。

2.优点

        在不增加参数的情况下，增加了图像的感受野；缺点：局部信息丢失：由于空洞卷积的计算方式类似于棋盘格式，某一层得到的卷积结果，来自上一层的独立的集合，没有相互依赖，因此该层的卷积结果之间没有相关性，即局部信息丢失。远距离获取的信息没有相关性：由于空洞卷积稀疏的采样输入信号，使得远距离卷积得到的信息之间没有相关性，影响分类结果