多项式回归
文章目录
- 前言
- 一、什么是多项式回归?
- 二、sklearn中的多项式回归与pipeline
-
- 1、引用sklearn中的多项式回归
- 2、关于PolynorizedFeatures
- 3、关于Pipeline
- 总结
前言
对于线性回归,有一个限制条件,就是我们需要假设数据之间呈线性关系。
那如果数据是非线性关系呢?
这一节我们来讲解多项式回归问题。
其实对于多项式回归,我们也可以运用线性回归的思路
一、什么是多项式回归?
比如一个二次曲线,虽然我们也可以用线性回归来拟合,但是效果一定不好

如:
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,4,size=100)
plt.scatter(x,y)
plt.show()
如假设有线性关系:
from sklearn.linear_model import LinearRegression
reg=LinearRegression()
reg.fit(X,y)
y_predict=reg.predict(X)
plt.scatter(x,y)
plt.plot(x,y_predict,color='r')

拟合效果并不好
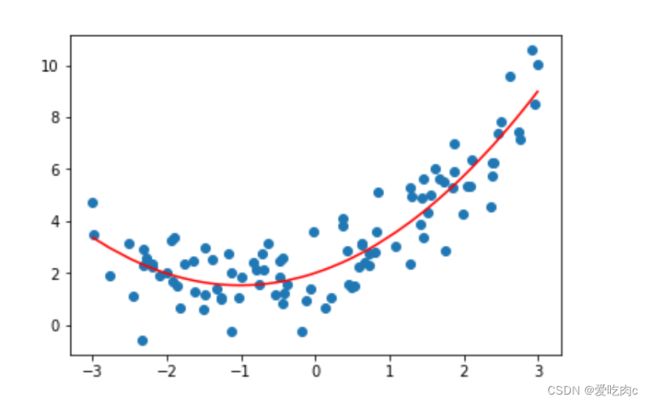
我们可以把X的平方当成一个特征,此时就可以把多项式回归简化成线性回归问题
X2=np.hstack([X,X**2])
reg2=LinearRegression()
reg2.fit(X2,y)
y2_predict=reg2.predict(X2)
plt.scatter(x,y)
#x是无序的,所以需要排序,那么y也需要相对应
plt.plot(np.sort(x),y2_predict[np.argsort(x)],color='r')
reg2.coef_
可以看到X的平方系数约为1,X的系数约为0.5 ,与我们y的求法中的系数是大致相同的。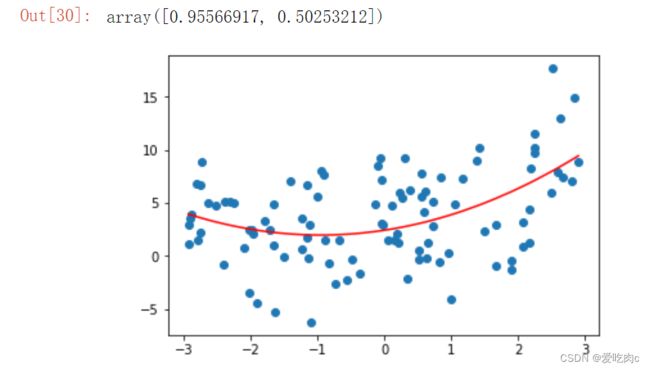
二、sklearn中的多项式回归与pipeline
1、引用sklearn中的多项式回归
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
from sklearn.preprocessing import PolynomialFeatures
poly=PolynomialFeatures(degree=2) #代表我们最多要x的多少次方
poly.fit(X)
X2=poly.transform(X) #注意PolynomialFeatures 会自动帮我们添上 X的0次方(系数全为1),x的1次方即x,x的平方 所以此时X2为3列,而不是2列
from sklearn.linear_model import LinearRegression
reg=LinearRegression()
reg.fit(X2,y)
y_predict=reg.predict(X2)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
2、关于PolynorizedFeatures
x=np.arange(1,11).reshape(-1,2)
poly=PolynomialFeatures(degree=3)
poly.fit(x)
x3=poly.transform(x)
x3.shape
(5, 10)
x本身是2列 添加一个全为1 的x0 之后x2有3列 x3有4列 共10列

3、关于Pipeline
pipeline为管道的意思,通过pipeline我们可以将多项式回归封装起来执行,pipeline中传入的一个列表,即是我们这个管道的每一个步骤对应的类。列表中的每一个元素是一个元组,元组中的第一个元素是一个字符串即实例化的类名,第二个参数是我们使用的类名。
包括三个步骤 1、多项式回归 2、数据均值方差归一化3、线性回归
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
pip_line=Pipeline([
("poly",PolynomialFeatures(degree=2)),
("sca_std",StandardScaler()),
("reg",LinearRegression())
])
pip_line.fit(X,y)
y_predict=pip_line.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
总结
下节讲解 过拟合与欠拟合