关键词提取(keyword extraction)技术
目录
- 1 统计方法(Statistical Method)
-
- 1.1 TF
- 1.2 TFIDF
- 1.3 YAKE
- 2 图方法(Graph Based Approaches)
-
- 2.1 PageRank
- 2.2 TextRank
- 2.2 SingleRank
- 2.3 TopicRank
- 2.4 PositionRank
- 3 语义模型(Semantic Models)
1 统计方法(Statistical Method)
基于统计方法的核心思想就是计算文本中每个term的分值,有了分值,就可以对所有的term进行排序,然后获取top n个分值最大的term作为文本的关键词。不同的统计方法计算每个term的分值方式不同。
1.1 TF
Term-Frequency(TF)词频是最简单的一种方法,通过词在文档里出现的频率进行分值计算。虽然方法简单,却是一种很有效的方法获取文档中的重要主题topics。每个term的分值计算如下:
t f w o r d = N w o r d N a l l tf_{word} = \frac{N_{word}}{N_{all}} tfword=NallNword
其中, N w o r d N_{word} Nword表示该词在文本中出现的次数, N a l l N_{all} Nall表示整个文本的单词频率数。
基于词频的主要问题在于,没有考虑结构化和语义信息,同时也不能区分同义词,而且有些停用词在所有文档出现的频率都很高。
1.2 TFIDF
TF-IDF是一种很简单但却很有效的方法,计算文本中的每个term会考虑两个因素。一是term本身在文档中的词频,这就是上小结提到的TF,另一个是倒文本频率(Inverse Document Frequency)IDF,这个指标衡量的是有多少文本包含了该term。IDF主要用来惩罚那些在很多文本中都有出现的term,往往这些term都是一些无关紧要的停用词等。
TF-IDF的数学公式如下:
t f i d f w o r d = t f w o r d ∗ l o g ( D D w o r d ) tfidf_{word} = tf_{word} * log(\frac{D}{D_{word}}) tfidfword=tfword∗log(DwordD)
其中 D D D表示整个文档的数量。 D w o r d D_{word} Dword表示包含该word的文档数量,从公式可以看出, D w o r d D_{word} Dword越大,整个分值就越小。tfidf整个核心思想就是,term在一个文档的重要程度取决于该term在该文档的频率和在其它文档的出现的次数。
1.3 YAKE
A Text Feature Based Automatic Keyword
Extraction Method for Single Documents
YAKE(Yet Another Keyword Extractor)是一种无监督的关键词提取算法,特征提取主要考虑五个因素(去除停用词后):
- 大写term(Casing):大写字母的term(除了每句话的开头单词)的重要程度比那些小写字母的term重要程度要大
T c a s e = m a x ( T F u , T F a ) T F T_{case} = \frac{max(TF_u, TF_a)}{TF} Tcase=TFmax(TFu,TFa)
其中, T F u TF_u TFu表示该词的大写次数, T F a TF_a TFa表示该词的缩写次数。 - 词的位置(Word Position):文本越开头的部分句子的重要程度比后面的句子重要程度要大
T p o s i t i o n = l o g 2 ( l o g 2 ( 2 + M e d i a n ( S e n t ) ) ) T_{position} = log_2(log_2(2 + Median(Sen_t))) Tposition=log2(log2(2+Median(Sent)))
其中 M e d i a n ( S e n t ) Median(Sen_t) Median(Sent)表示包含该词的所有句子在文档中的位置中位数。 - 词频(Term Frequency): 一个词在文本中出现的频率越大,相对来说越重要,同时为了避免长文本词频越高的问题,会进行归一化操作
T F n o r m = T F ( t ) M e a n T F + 1 ∗ σ TF_{norm} = \frac{TF_{(t)}}{MeanTF + 1*\sigma} TFnorm=MeanTF+1∗σTF(t)
其中,MeanTF是整个词的词频均值, σ \sigma σ是标准差 - 上下文关系(Term Related to Context):一个词与越多不相同的词共现,该词的重要程度越低
D L [ D R ] = ∣ A t , w ∣ ∑ k ∈ A t , w C o O c c u r t , k DL[DR] = \frac{\begin{vmatrix}A_{t,w} \end{vmatrix}}{\sum_{k\in A_{t,w}}CoOccur\text{ } t,k} DL[DR]=∑k∈At,wCoOccur t,k∣ ∣At,w∣ ∣
T R e l = 1 + ( D L + D R ) ∗ T F ( t ) M a x T F T_{Rel} = 1 + (DL +DR) * \frac{TF(t)}{MaxTF} TRel=1+(DL+DR)∗MaxTFTF(t)
其中 D L DL DL表示窗口size为 w w w从左边滑动, D R DR DR表示从右边滑动。 ∣ A t , w ∣ \begin{vmatrix}A_{t,w} \end{vmatrix} ∣ ∣At,w∣ ∣表示出现在固定窗口大小为 w w w下,出现不同的词的个数。 M a x T F MaxTF MaxTF表示所有词频的最大值。 - 词在句子中出现的频率(Term Different Sentence):一个词在越多句子中出现,相对更重要
T S e n t e n c e = S F ( t ) S e n t e n c e a l l T_{Sentence} = \frac{SF(t)}{Sentence_{all}} TSentence=SentenceallSF(t)
其中 S F ( t ) SF(t) SF(t)是包含词 t t t的句子频率, S e n t e n c e a l l Sentence_{all} Sentenceall表示所有句子数量。
最后计算每个term的分值公式如下:
S ( t ) = T R e l ∗ T P o s i t i o n T c a s e + T F n o r m T R e l + T S e n t e n c e T R e l S(t) = \frac{T_{Rel}*T_{Position}}{T_{case}+\frac{TF_{norm}}{T_{Rel}}+\frac{T_{Sentence}}{T_{Rel}}} S(t)=Tcase+TRelTFnorm+TRelTSentenceTRel∗TPosition
S ( t ) S(t) S(t)表示的是单词 t t t的分值情况,其中 s ( t ) s(t) s(t)分值越小,表示的单词 t t t越重要。
2 图方法(Graph Based Approaches)
2.1 PageRank
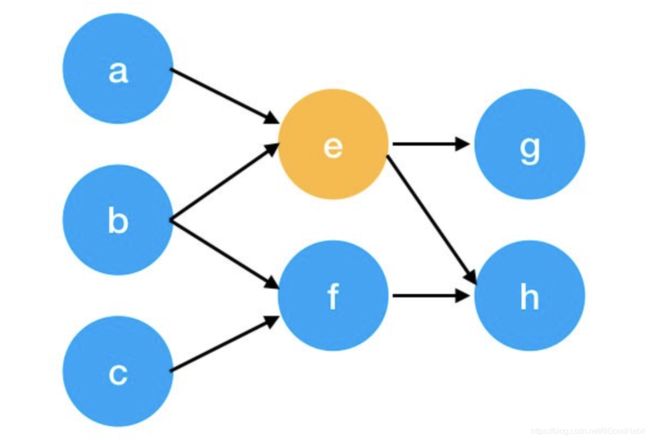
在介绍TextRank之前,让我们先来回顾下PageRank,假设有如下图:
计算每个节点的公式如下:
S ( V i ) = ( 1 − α ) ∣ V ∣ + α ∗ ∑ V j ∈ I n ( V i ) 1 ∣ O u t ( V j ) ∣ S ( V j ) S(V_i) = \frac{(1-\alpha)}{|V|} + \alpha* \sum_{V_j \in In(V _i)} \frac{1}{\begin{vmatrix}Out(V_j)\end{vmatrix}}S(V_j) S(Vi)=∣V∣(1−α)+α∗Vj∈In(Vi)∑∣ ∣Out(Vj)∣ ∣1S(Vj)
其中 S ( V i ) S(V_i) S(Vi)表示网页 i i i的权重分值, I n ( V i ) In(V_i) In(Vi)表示指向节点 V i V_i Vi的节点, O u t ( V j ) Out(V_j) Out(Vj)表示节点 V j V_j Vj指出的节点。 ∣ O u t ( V j ) ∣ \begin{vmatrix}Out(V_j)\end{vmatrix} ∣ ∣Out(Vj)∣ ∣表示节点 V j V_j Vj指出节点的总数。为了保证PageRank(或者随机游走)不会死循环到一个环出不来,增加了一个随机因子 α \alpha α, α \alpha α表示不进行随机跳转的概率。让我们看看,上图节点 e e e的权重分值计算过程。
首先我们可以用一个矩阵表示图中节点 a , b , e , f a, b, e, f a,b,e,f的连接关系:
| a | b | e | f | |
|---|---|---|---|---|
| a | 0 | 0 | 0 | 0 |
| b | 0 | 0 | 0 | 0 |
| e | 1 | 1 | 0 | 0 |
| f | 0 | 1 | 0 | 0 |
每一行代表该指向该节点的节点,每一列代表该节点指向其它的节点。根据上面的公式 1 ∣ O u t ( V i ) ∣ \frac{1}{\begin{vmatrix}Out(V_i)\end{vmatrix}} ∣Out(Vi)∣1,需要对每一列进行归一化,所以调整如下:
| a | b | e | f | |
|---|---|---|---|---|
| a | 0 | 0 | 0 | 0 |
| b | 0 | 0 | 0 | 0 |
| e | 1 | 0.5 | 0 | 0 |
| f | 0 | 0.5 | 0 | 0 |
然后我们用这个矩阵去乘以每个节点的权重,最开始,每个节点的权重初始化都为1,如下计算:
[ 0 0 0 0 0 0 0 0 1 0.5 0 0 0 0.5 0 0 ] ∗ [ 1 1 1 1 ] = [ 0 0 1.5 0.5 ] \begin{bmatrix}0 &0 &0 &0\\ 0 & 0 & 0 &0 \\ 1& 0.5 & 0 &0\\0& 0.5 & 0 &0\end{bmatrix} * \begin{bmatrix} 1 \\ 1 \\1 \\1 \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 1.5 \\ 0.5 \end{bmatrix} ⎣ ⎡0010000.50.500000000⎦ ⎤∗⎣ ⎡1111⎦ ⎤=⎣ ⎡001.50.5⎦ ⎤
这只是一次迭代,加入衰减因子 α \alpha α,python迭代多次结果如下:
# -*-coding:utf8 -*-
import sys
import numpy as np
def pagerank(graph):
'''
简单实现pagerank迭代过程
'''
pr = np.array([1, 1, 1, 1]) #init node
a = 0.85
for iter in range(10):
pr = (1-d) + d * np.dot(graph, pr)
print(iter)
print(pr)
if __name__=='__main__':
graph = np.array([[0,0,0,0],
[0,0,0,0],
[1, 0.5, 0, 0],
[0,0.5,0,0]])
pagerank(graph)
output:

最后节点 e e e的PageRank分值为0.34125。
2.2 TextRank
TextRank: Bringing Order into Texts
TextRank算法是基于PageRank算法,PageRank算法,其中图的节点是网页,而TextRank是词。
最原始的PageRank算法是无权重的图,而TextRank是有权重的图。因此,节点的权重分值计算和PageRank比变动如下:
W S ( V i ) = ( 1 − α ) ∣ V ∣ + α ∗ ∑ V j ∈ I n ( V i ) w j i ∑ v k ∈ O u t ( V j ) w j k W S ( V j ) WS(V_i) = \frac{(1-\alpha)}{|V|} + \alpha* \sum_{V_j \in In(V_i)} \frac{w_{ji}} {\sum_{v_k \in Out(V_j) }w_{jk}} WS(V_j) WS(Vi)=∣V∣(1−α)+α∗Vj∈In(Vi)∑∑vk∈Out(Vj)wjkwjiWS(Vj)
其中 w i j w_{ij} wij表示了节点 V j V_j Vj与节点 V j V_j Vj之间的边连接权重。
接下来看TextRank算法的步骤流程:
- 预处理:文本分词,然后用标注工具进行标注,获取重要的词性
- 构建图:将处理后的词作为图的节点,边根据这些词是否在一个滑动窗口共现,进行边的连接。初始各节点权重都为1,然后用上述计算公式进行迭代
- 计算分值:所有unigrams(节点)权重分值计算完后,选取top个节点,再根据设置的窗口大小,计算更高的n-gram关键词分值,最后根据分值,获取top K个关键词
2.2 SingleRank
CollabRank: Towards a Collaborative Approach to Single-Document Keyphrase Extraction
SingleRank是PageRank的变体,主要有两个变化:
- 第一:不同于PageRank,每个边都有相同的分值,SingleRank会根据窗口大小词之间的距离计算不同的边权重
- 第二:与TextRank不同的是,SingleRank保留所有的unigrams词,然后类似TextRank方法,滑动窗口方式计算更高的n-grams词,背后的原理是,两个分值较低的unigram,有可能产生较高分值的bi-gram。
2.3 TopicRank
TopicRank: Graph-Based Topic Ranking for Keyphrase Extraction
TopicRank把主题当做相似关键短语的簇,这些topics会根据在文档的重要性进行排序,然后选取top 个最相关的topics,每个topic选择一个最重要的关键短语来代表文档的核心关键词。
TopicRank算法的步骤如下:
- 主题识别:主要抽取名词短语来表征文档的主题,短语中有超过25%重合的单词就考虑为相似短语,用 Hierarchical Agglomerative Clustering (HAC) algorithm进行了聚类相似的短语。
- 图构建:这里的图中的节点是topics,边的权重,根据两个topics t i , t j t_i, t_j ti,tj之间的语义关系进行分配,而语义关系的强弱根据两个主题的关键短语之间的距离公式,具体计算如下:
w i , j = ∑ c i ∈ t i ∑ c j ∈ t j d i s t ( c i , c j ) w_{i,j} = \sum_{c_i \in t_i} \sum_{c_j \in t_j} dist(c_i, c_j) wi,j=ci∈ti∑cj∈tj∑dist(ci,cj)
d i s t ( c i , c j ) = ∑ p i ∈ p o s ( c j ) ∑ p j ∈ p o s ( c j ) 1 ∣ p i − p j ∣ dist(c_i, c_j) = \sum_{p_i \in pos(c_j)} \sum_{p_j \in pos(c_j)} \frac{1}{\begin{vmatrix} p_i-p_j \end{vmatrix}} dist(ci,cj)=pi∈pos(cj)∑pj∈pos(cj)∑∣ ∣pi−pj∣ ∣1
其中 d i s t ( c i , c j ) dist(c_i, c_j) dist(ci,cj)表示关键短语 c j c_j cj和 c j c_j cj在文档中的偏移距离。 p o s ( c i ) pos(c_i) pos(ci)表示关键短语 c i c_i ci的所有偏移位置。TopicRank不需要设置窗口,而是通过计算位置偏移距离。 - 关键短语选择:一旦topic进行排序后,选择top K个topics,每个topic选择一个最重要的关键短语作为输出,所有topics总共产生top K个关键短语。有三个策略选择一个topic最适合的关键短语:第一:选择关键短语中最开始出现在文档的那个关键短语;第二:选择频率最高的那个关键短语;第三:选择聚焦的群簇中心的那个关键短语
2.4 PositionRank
PositionRank: An Unsupervised Approach to Keyphrase Extraction from Scholarly Documents
PositionRank也是一种基于图结构的算法,根据词的位置和词频来计算每个词的分值。算法主要三个部分组成:
- 图的构建:类似TextRank,根据POS选择关键词构建图的节点,节点的边根据窗口size共现次数来计算两个词的边的权重分值。
- Position-Biased PageRank
假设 G G G是一个按照上述方法构建的无方向图, M M M是它的邻接矩阵, m i j ∈ M m_{ij} \in M mij∈M是节点 ( v i , v j ) (v_i, v_j) (vi,vj)之间的边的权重,若不存在边,则为0。PageRank计算节点 v i v_i vi的分值,是不断迭代计算所有指向 v i v_i vi节点的分值之和。
令 S S S为PageRank分值,对于所有 v i ∈ V v_i \in V vi∈V的节点,初始 S S S每个元素值都为 1 ∣ V ∣ \frac{1}{\begin{vmatrix} V \end{vmatrix}} ∣V∣1。PageRank在 t + 1 t+1 t+1步计算每个节点的分值迭代公式如下:
S ( t + 1 ) = M ~ . S ( t ) S(t+1) = \tilde M . S(t) S(t+1)=M~.S(t)
其中 M ~ \tilde M M~ 是矩阵 M M M归一化矩阵,其中 m i j ~ ∈ M ~ \tilde{m_{ij}} \in \tilde M mij~∈M~定义如下:
m i j ~ = { m i j / ∑ j = 1 ∣ V ∣ m i j i f ∑ j = 1 ∣ V ∣ m i j ≠ 0 0 o t h e r w i s e \tilde{m_{ij}} = \begin{cases} m_{ij} / \sum_{j=1}^{\begin{vmatrix} V \end{vmatrix}} m_{ij} \text{ }\text{ } if \sum_{j=1}^{\begin{vmatrix} V \end{vmatrix}}m_{ij}\ne 0 \\\\ 0 \text{ } \text{ } otherwise \end{cases} mij~=⎩ ⎨ ⎧mij/∑j=1∣V∣mij if∑j=1∣V∣mij=00 otherwise
为了保证PageRank(或者随机游走)不会死循环到一个环出不来,一个衰减因子 a a a允许跳入到任何一个节点中去。所以迭代更新公式如下:
S = a . M ~ . S + ( 1 − a ) . p ~ S = a. \tilde M. S + (1-a).\tilde p S=a.M~.S+(1−a).p~
其中 p ~ \tilde p p~是一个长度为 ∣ V ∣ \begin{vmatrix} V \end{vmatrix} ∣ ∣V∣ ∣,每个元素值为 1 ∣ V ∣ \frac{1}{\begin{vmatrix} V \end{vmatrix}} ∣V∣1的向量。
Position-Biased PageRank会根据每个词的位置的导数计算权重,若一个词出现在文档多个位置,则分值相加。核心思想是:越在一个文档靠前的位置,权重越大,同时频率出现越高,权重也越大。
假设一个词在文档的位置时第二,第五,第10,则权重分值为:1/2+1/5+1/10=0.8。再进行归一化,则向量 p ~ \tilde p p~的计算公式如下:
p ~ = [ p 1 p 1 + p 2 + . . . + p ∣ V ∣ , p 2 p 1 + p 2 + . . . + p ∣ V ∣ , . . . , p v p 1 + p 2 + . . . + p ∣ V ∣ ] \tilde p = \begin{bmatrix} \frac{p_1}{p_1+p_2+...+p_{\begin{vmatrix} V\end{vmatrix}}} , \frac{p_2}{p_1+p_2+...+p_{\begin{vmatrix} V\end{vmatrix}}} , ...,\frac{p_v}{p_1+p_2+...+p_{\begin{vmatrix} V\end{vmatrix}}} \end{bmatrix} p~=[p1+p2+...+p∣V∣p1,p1+p2+...+p∣V∣p2,...,p1+p2+...+p∣V∣pv]
最后迭代计算公式如下:
S ( v i ) = ( 1 − a ) . p i ~ + a . ∑ v j ∈ A d j ( v i ) w j i O ( v j ) S ( v j ) S(v_i) = (1-a). \tilde{p_i} +a . \sum_{v_j \in Adj(v_i)} \frac{w_{ji}}{O(v_j)} S(v_j) S(vi)=(1−a).pi~+a.vj∈Adj(vi)∑O(vj)wjiS(vj)
其中 O ( v j ) = ∑ v k ∈ A d j ( v j ) w j k O(v_j) = \sum_{v_k \in Adj(v_j)}w_{jk} O(vj)=∑vk∈Adj(vj)wjk, p i ~ \tilde{p_i} pi~是向量 p ~ \tilde p p~节点为 v i v_i vi的权重。
当相邻两次迭代差异很小,或者迭代达到一个最大迭代次数时,则停止迭代。
3 语义模型(Semantic Models)
基于语义模型的关键词或者短语提取,一般是有监督学习,把关键词提取当做一个标注任务,判断该词是关键词还是不是关键词;或者通过对文本进行分类,基于attention层自动学习文本中的每个词的权重分值,根据分值高低提取关键词。这些方法都是有监督学习,训练模型需要有标签的数据。
- Keyphrase Extraction Using Deep Recurrent Neural Networks on Twitter
该论文发表在2016年 EMNLP上,本文基于一个2层的RNN模型将关键词和关键短语提取当做一个标注分类任务,判断每个词是否是关键词或者关键短语。模型的第一层用来做关键词识别任务,第二层用来做关键短语识别任务,最后将两个任务损失函数进行权重融合,作为最终的损失函数:
J ( θ ) = a J 1 ( θ ) + ( 1 − a ) J 2 ( θ ) J(\theta) = aJ_1(\theta) + (1-a)J_2(\theta) J(θ)=aJ1(θ)+(1−a)J2(θ) - Progress Notes Classification and Keyword
Extraction using Attention based Deep Learning
Models with BERT
本论文基于BERT+attention Layer通过对文本进行分类,利用attention层自动学习文本中的每个词的权重,根据词的权重,可以获取与文本主题相关的关键词,下图是截取论文中提供的高attention权重的关键词效果:

更多关于关键词,term weight分值计算,可以参考我的另外一篇blog: 词权重 (term weight) 方法总结
附上一个关键词提取Tools:The 6 Best Keyword Extraction Tools & How to Use Them