VAE总结
这段时间看了VAE的有关知识,但网上关于VAE的讲解较为理论复杂,我这里就记录一下自己的想法了。
定义
VAE从概率的角度描述隐空间与输入样本,它将样本的隐变量建模为概率分布, 而非像AE一样把隐变量看做是离散的值。
AE VS VAE
损失函数
我们假设隐变量的概率分布为标准正态分布 N ( 0 , 1 ) N(0, 1) N(0,1)(这种分布不是必须的,也可以是其它分布)。而描述正态分布需要有两个参数 μ x , σ x \mu_x, \sigma_x μx,σx,在encoder端使用神经网络来拟合这两个参数。在decoder端,使用神经网络来还原出原始图像。因此,VAE的损失函数分为两部分:
-
正则化项,也就是KL Loss
-
重构损失
L = L R e c o n + L K L = ∥ x − x ^ ∥ 2 + K L [ N ( μ x , σ x ) , N ( 0 , 1 ) ] = ∥ x − d ( z ) ∥ 2 + K L [ N ( μ x , σ x ) , N ( 0 , 1 ) ] \begin{aligned} L &= L_{Recon} + L_{KL} \\ &= \|x-\hat{x}\|^{2}+\mathrm{KL}[N(\mu_{x}, \sigma_{x}), N(0, 1)] \\ &= \|x-d(z)\|^{2}+K L[N(\mu_{x}, \sigma_{x}), N(0, 1)] \end{aligned} L=LRecon+LKL=∥x−x^∥2+KL[N(μx,σx),N(0,1)]=∥x−d(z)∥2+KL[N(μx,σx),N(0,1)]
关于 K L [ N ( μ x , σ x ) , N ( 0 , 1 ) ] K L\left[N\left(\mu_{x}, \sigma_{x}\right), N(0,1)\right] KL[N(μx,σx),N(0,1)]的推导如下:
K L ( N ( μ , σ 2 ) ∥ N ( 0 , 1 ) ) = ∫ 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 ( log e − ( x − μ ) 2 2 σ 2 2 π σ 2 e − x 2 2 2 π ) d x = ∫ 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 log { 1 σ 2 exp { 1 2 [ x 2 − ( x − μ ) 2 σ 2 ] } } d x = 1 2 ∫ 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 [ − log σ 2 + x 2 − ( x − μ ) 2 σ 2 ] d x = 1 2 ( − log σ 2 + μ 2 + σ 2 − 1 ) \begin{aligned} & K L\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right) \\ =& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}} }\left(\log \frac{\frac{e^{ \frac{-(x-\mu)^{2}}{2 \sigma^{2}} }}{\sqrt{2 \pi \sigma^{2}}} }{\frac{e^{\frac{-x^{2}}{2}}}{\sqrt{2 \pi}} }\right) d x \\ =& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}} } \log \left\{\frac{1}{\sqrt{\sigma^{2}}} \exp \left\{\frac{1}{2}\left[x^{2}- \frac{(x-\mu)^{2}}{\sigma^{2}} \right]\right\}\right\} d x \\ =& \frac{1}{2} \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}} }\left[-\log \sigma^{2}+x^{2}- \frac{(x-\mu)^{2}}{\sigma^{2}} \right] d x \\ =& \frac{1}{2}\left(-\log \sigma^{2}+\mu^{2}+\sigma^{2}-1\right) \end{aligned} ====KL(N(μ,σ2)∥N(0,1))∫2πσ21e2σ2−(x−μ)2⎝⎜⎜⎛log2πe2−x22πσ2e2σ2−(x−μ)2⎠⎟⎟⎞dx∫2πσ21e2σ2−(x−μ)2log{σ21exp{21[x2−σ2(x−μ)2]}}dx21∫2πσ21e2σ2−(x−μ)2[−logσ2+x2−σ2(x−μ)2]dx21(−logσ2+μ2+σ2−1)
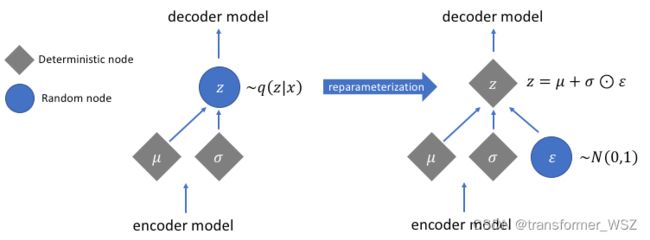
重参数技巧
我们从概率分布中采样出 z z z ,但是该过程是不可导的。VAE通过重参数化使得梯度不因采样而断裂。
总结
其实VAE可以看成一个做降维的model,我们希望把一个高维的特征投影到一个低维的流型上。而在VAE中,这个低维流型就是一个多元标准正态分布。为了使投影准确,于是通过希望每一个样本 X i X_i Xi的计算出来的期望与方差都接近与我们希望投影的分布,所以这里就有了相KL Loss。至于重构损失,是可以使采样的时候更加准确,能够采样到我们在encode的时候投影到的点。
最佳实践
Pytorch实现: VAE 这篇博客实现了VAE,整体上代码简单易懂。在generation阶段,我们只需从学习到的概率分布中采样,然后送入decoder中解码,即可获得生成的图片。
参考
-
变分自编码器VAE:原来是这么一回事
-
Understanding Variational Autoencoders (VAEs)
-
Pytorch实现: VAE
-
变分自编码器入门
-
VAE.ipynb - Colaboratory
-
李宏毅2021春机器学习课程
-
VAE (ntu.edu.tw)
-
VAE的推导