数理统计——KNN分类与预测
文章目录
- 前言
- 一、相关概念
-
- 1.算法原理
- 2.算法超参数
- 3.算法步骤
- 4.距离如何度量?
- 5.KD树
- 6.权重计算方式
- 二、使用KNN实现分类
- 三、使用KNN回归预测
前言
- 学习KNN算法的原理;
- 超参数调整;
- KNN算法的应用;
一、相关概念
先来看一个例子:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"]="SimHei"
plt.rcParams["axes.unicode_minus"]=False
plt.rcParams["font.size"]=12
good=np.array([[95,93],[90,92],[91,96]])
medium=np.array([[85,82],[83,87],[80,84]])
bad=np.array([[61,69],[66,63],[72,65]])
unknow=np.array([[83,77]])
plt.scatter(good[:,0],good[:,1],color="r",label="优等生")
plt.scatter(medium[:,0],medium[:,1],color="g",label="中等生")
plt.scatter(bad[:,0],bad[:,1],color="b",label="差等生")
plt.scatter(unknow[:,0],unknow[:,1],color="orange",label="未知")
plt.legend()
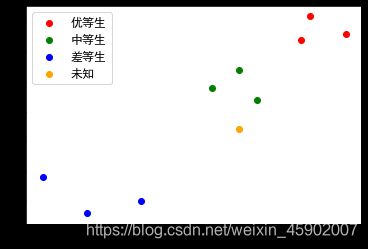
对于橙色未知的数据,我们可以把它归为哪一类呢?因为距离绿色也就是中等生比较近,所以我们觉得更可能是80-90的范围。这也是knn算法的思想。
1.算法原理
“近朱者赤近墨者黑”,相似度较高的样本,映射到n维空间之后,其距离会比相似度较低的样本在距离上更接近,这就是KNN算法的核心思维。
KNN(K-Nearest Neighbor)即k近邻算法,k近邻即K个最近的邻居,当需要一个未知样本的时候,就由与该样本最接近的k个邻居来决定。KNN既可用于回归也可以用于分类问题。
- 用于分类时,使用k个邻居中,类别数量(或加权最多)者,作为预测结果;
- 用于回归时,使用k个邻居的均值(或加权均值)作为预测结果;
2.算法超参数
超参数是指在训练模型的之前,需要人为指定的参数,超参数不像在模型内部获得的参数是在训练过程中获得,它需要提前指定,对 模型的效果有很大影响。
K值:其选择过小,模型过于依赖于附近邻居样本,具有较好敏感性,但是稳定性弱,容易过拟合;k值过大,稳定性增加,但敏感性减弱,容易导致欠拟合。
如何获得合适的值:使用交叉验证(即大部分样本数据用与训练集,小部分用于测试集,来验证分类模型的准确性)。我们一般把k值选取在较小的范围,同时在验证集上准确率最高的那一个最近确定为k值。
3.算法步骤
1、确定算法超参数:
- 确定近邻的数量k;
- 确定距离度量方式;
- 确定权重计算方式;
2、对于k个最近的邻居,他们属于哪个分类最多,待分类物体就属于哪一类。
4.距离如何度量?
-
闵可夫斯基距离: 不是一个距离,而是一组距离的定义,当p=1,就是曼哈顿距离,当p=2,就是欧氏距离,当p趋于无穷大就是切比雪夫距离。在sklearn中默认使用的就是这个距离计算方式。

-
切比雪夫距离:两个点坐标数值差的绝对值的最大值,max(|x1-y1|,|x2-y2|)。
-
余弦距离:实际上计算的是两个向量的夹角,是在方向上计算两者之间的差异,对数值不敏感。在兴趣相关上,角度关系比距离的绝对值更重要,因此余弦距离可以用来衡量用户对内容感兴趣的区分度。(比如搜索推荐)
5.KD树
为了减少计算距离次数,提升 KNN 的搜索效率,人们提出了 KD 树(K-Dimensional 的缩写)。KD 树是对数据点在 K 维空间中划分的一种数据结构。在 KD 树的构造中,每个节点都是 k 维数值点的二叉树。既然是二叉树,就可以采用二叉树的增删改查操作,这样就大大提升了搜索效率。在sklearn中可以直接调用。
6.权重计算方式
- 统一权重:所有样本权重相同
- 距离加权权重:样本的权重与待预测样本的距离成反比。
二、使用KNN实现分类
以鸢尾花数据集为例,通过knn算法实现分类任务。为了方便,只取其中两个特征。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
iris=load_iris()
x=iris.data[:,:2]
y=iris.target
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25,random_state=0)
knn=KNeighborsClassifier(n_neighbors=3,weights="uniform")
knn.fit(x_train,y_train)
y_hat=knn.predict(x_test)
print(classification_report(y_test,y_hat))
输出:
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.78 0.44 0.56 16
2 0.44 0.78 0.56 9
accuracy 0.71 38
macro avg 0.74 0.74 0.71 38
weighted avg 0.77 0.71 0.71 38
不同的超参数值,对模型的分类效果影响不同,我们通过决策边界来看一下:
from matplotlib.colors import ListedColormap
def plot_decision_boundary(model,x,y):
color=["r","g","b"]
marker=["o","v","x"]
class_label=np.unique(y)
cmap=ListedColormap(color[:len(class_label)])
x1_min,x2_min=np.min(x,axis=0)
x1_max,x2_max=np.max(x,axis=0)
x1=np.arange(x1_min-1,x1_max+1,0.02)
x2=np.arange(x2_min-1,x2_max+1,0.02)
x1,x2=np.meshgrid(x1,x2)
z=model.predict(np.c_[x1.ravel(),x2.ravel()])
z=z.reshape(x1.shape)
plt.contourf(x1,x2,z,cmap=cmap,alpha=0.5)
for i,class_ in enumerate(class_label):
plt.scatter(x=x[y==class_,0],y=x[y==class_,1],c=cmap.colors[i],label=class_,marker=marker[i])
plt.legend()
from itertools import product
weights=["uniform","distance"]
ks=[2,15]
plt.figure(figsize=(18,10))
#使用weights与ks的笛卡尔积组合,这样可以使用单层循环取代嵌套循环,增加代码可读性与可理解性:
for i,(w,k)in enumerate(product(weights,ks),start=1):
plt.subplot(2,2,i)
plt.title(f"k值:{k}权重:{w}")
knn=KNeighborsClassifier(n_neighbors=k,weights=w)
knn.fit(x,y)
plot_decision_boundary(knn,x_train,y_train)

通过决策边界可以看出,k值越小,模型敏感性越强,敏感性越弱,模型也就越复杂,容易过拟合;反之容易欠拟合。
在实际中很难通过直觉就能找到合适的超参数,这时可以通过网格交叉验证的方式找出效果最好的参数。
#网格验证寻找合适的参数
from sklearn.model_selection import GridSearchCV
knn=KNeighborsClassifier()
#定义需要尝试的超参数组合
grid={"n_neighbors":range(1,11,1),"weights":["uniform","distance"]}
gs=GridSearchCV(estimator=knn,param_grid=grid,scoring="accuracy",n_jobs=-11,cv=5,verbose=10,iid=True)
gs.fit(x_train,y_train)
输出:
Fitting 5 folds for each of 20 candidates, totalling 100 fits
略…………太多了
```python
#最好的分值
print(gs.best_score_)
#最好的参数组合
print(gs.best_params_)
#使用最好的超参数训练好的模型
print(gs.best_estimator_)
输出:0.8035714285714286
{'n_neighbors': 7, 'weights': 'uniform'}
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=7, p=2,
weights='uniform')
#使用最好的模型在测试集上进行测试,实现最后的经验
estimator=gs.best_estimator_
y_hat=estimator.predict(x_test)
print(classification_report(y_test,y_hat))
输出: precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.80 0.50 0.62 16
2 0.47 0.78 0.58 9
accuracy 0.74 38
macro avg 0.76 0.76 0.73 38
weighted avg 0.79 0.74 0.74 38
三、使用KNN回归预测
使用波士顿房价数据集进行KNN算法回归预测,同时使用线性回归算法进行比较:
from sklearn.datasets import load_boston
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
knn.fit(X_train, y_train)
print("KNN算法R^2值:", knn.score(X_test, y_test))
lr = LinearRegression()
lr.fit(X_train, y_train)
print("线性回归算法R^2值:", lr.score(X_test, y_test))
从结果可以看出,使用KNN算法进行回归效果比线性回归要差,但不能证明KNN算法不如线性回归,原因在于KNN在训练参数的时候,是基于距离来计算的,而线性回归不是,也就是说,如果特征之间量纲(数量级)不同,量纲较大的就会占据主导地位,从而算法会忽略量纲较小的,因此最终会影响到模型拟合效果,但线性回归不受影响。
不止KNN,还有很多算法都是如此,因此使用算法之前,需要将数据转化为相同的量纲,我们称这个过程叫做数据标准化。
在sklearn中,常用的标准化方式是均值标准差(StandardScaler)和最小最大值标准差(MinMaxScaler)
from sklearn.preprocessing import StandardScaler, MinMaxScaler
scaler = [StandardScaler(), MinMaxScaler()]
desc = ["均值标准差标准化", "最小最大值标准化"]
for s, d in zip(scaler, desc):
X_train_scale = s.fit_transform(X_train)
X_test_scale = s.transform(X_test)
knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
knn.fit(X_train_scale, y_train)
print(d, knn.score(X_test_scale, y_test))
输出:
均值标准差标准化 0.6248800677762865
最小最大值标准化 0.6177749492293981
可以看到经过标准化处理之后,模型效果有了很大的提升。
流水线(略)
KD树
函数构造中的重要参数,见图片中第二部分。
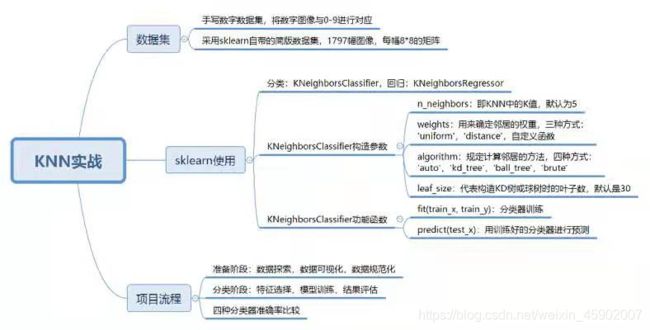
作业题:
1、在鸢尾花数据集中,使用KNN与逻辑回归进行比较,并绘制二者的ROC曲线,衡量效果。
2、思考KNN是怎样预测概率的?
3、对最后的程序调参,找到最好的参数 ?


