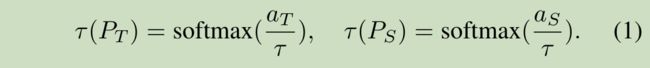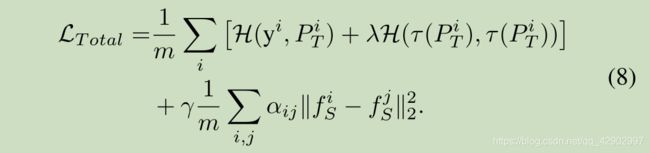knowledge distillation论文阅读之:Learning Student Networks via Feature Embedding
文章目录
- ABSTRACT
- INTRODUCTION
- RELATED WORK
-
- Network Trimming
- Layer Decomposition
- Knowledge Distillation
- STUDENT NETWORK EMBEDDING
-
- Teacher-student Interactions
- Locality Preserving Loss
ABSTRACT
- 知识蒸馏的本质是将 knowledge 从 teacher 网络 迁移到 student 网络,在经典的 KD 中,通常使用的方法是首先训练 teacher 网络,然后使用它的 logits 层输出为 soft target 来引导 student 网络学习
- 有些人认为 不仅是 logits 层能够引导 student 训练,在 teacher 网络的中间层的特征信息也能够对 student 网络的训练有指导作用。因此有人使用引入一个 intermediate layer (本质就是一个全连接的神经网络)来匹配 teacher 和 student 的中间层输出,从而达到将 teacher 的 知识引导 student 训练的目的。
- 但是这种方法存在明显的缺陷:这个 additional 的全连接层会引入大量的额外参数,使得整个网络的参数量急剧增长。对于放在边缘设备(例如手机等移动端),在内存方面会占用很多。
- 因此,本文提出了一种不使用全连接网络但是依然能达到将 teacher 网络中间层输出的 knowledge 迁移到 student 来指导 student 网络训练的目的。本文将其称为:引入一个 locality preserving loss 来鼓励 student 网络生成低维特征,这些低维特征可以继承教师网络中相应高维特征的固有属性。
- 本文给出了这个方法的理论公式,并且证明了这种方法在计算复杂度和空间复杂度上比全连接网络的优越性。
INTRODUCTION
- 目前很多方法尝试将 CNN 网络的模型参数进行压缩,这些方法有下面几类:
- quantization 量化
- weight and feature approximation 参数和特征逼近
- encoding 编码
- approximation 逼近
- pruning 剪枝
- 其中,基于权值修剪(weight pruning)的方法压缩性能最高,因为大多数预训练的 CNN中都存在相当大的精细权值(subtle weights)
- Han 等人的实验证明:AlexNet[2]中显示超过70%的细微权重可以删除而不影响其原来的 top-5 精度
- Wang等人[14]进一步指出,大权重和小权重都存在冗余,现代CNNs如ResNet[17]中也存在相当多的冗余。
- 虽然基于剪枝(pruning)的方法可以提供非常高的压缩和加速比,但利用这些方法压缩的CNN 不能直接在主流平台(如Tensorflow和Caffe)和硬件(如NVIDIA GPU卡)上使用,因为它们需要特殊的架构和实现技巧(如稀疏卷积和霍夫曼编码)。
- 由于更深层次的网络往往比浅层次的网络[18]具有更高的性能,因此出现了 teacher-student 学习范式[19]、[20]、[21]、[22]、[23]、[24]、[25]、[26] 等来训练可移植的网络(student 网络),这些可移植网络的结构更深,但参数和卷积滤波器比原始网络(student 网络)更少。
- 与其他方法相比,由 teacher-student 模式生成的可移植网络更加灵活,因为它们是完全规则的神经网络,不需要任何额外的支持来实现在线推理。
- 但是这种结构存在一个问题,就是 teacher 网络和 student 网络的参数量和结构相差巨大,因此除了使用最后的输出层 logits 来训练 student 网络之外, 对于 teacher 网络中间过程产生的信息,几乎无法有效利用来训练 student 网络。
- 因此,很多作品[21]、[22]、[23]、[24]、[25]、[26]提出使用额外设计的中间全连接层来调整维度,从而使得 teacher 中的提示层和 student 中的被引导层可以建立联系,从而达到训练 student 网络更好地训练效果
- 此外,全连通层引入了大量的辅助参数,这些参数具有较大的空间和计算复杂度,在实际应用中无法应用于大规模网络神经网络;例如:在 CNN 网络中,如果引入一个中间的全连接层来完成知识从 teacher 迁移到 student,那么这个中间全连接层产生的参数数量比 teacher 和 student 网络的参数之和还要多,在部署到移动终端上还是照样不现实的。
- 考虑到教师网络的高维特征和学生网络的低维特征,我们很自然地将这两个网络之间的信息传播视为一种特征嵌入任务。因此,我们提出了一种基于流形学习(manifold learning-based)的方法来训练轻便紧凑的 CNN 网络。总而言之,拟议的方法作出了以下贡献:
- 提出了一个特征嵌入的方法来实现 teacher 和 student 网络之间的连接;这样 filter 较少的学生网络就可以产生低维特征来保持 samples 之间的关系
- 引入一个 locality preserving loss 到 teacher-student 范式中,并从理论上证明了所提算法的较低计算复杂度
- 通过实验结果证明,该方法能够有效地训练可移植网络。
RELATED WORK
压缩模型的方式分为以下几种:
- 网络剪枝 network trimming
- 层分解 layer decomposition
- 知识蒸馏 knowledge distillation
Network Trimming
- 目的是为了去除冗余的神经元来加速和压缩原始的网络模型
- Gong 提出了 “向量量化(vector quantization)”的概念,使用一个聚类中心(cluster center)来表示相同的连接。
- Denton等人,探索如何使用奇异值分解(singular value decomposition)的方法,分解全连接层的权重矩阵
- 考虑到32位浮点数对于 CNN 、Courbariaux等网络来说太过于精确。[28]和Rastegari等人。[29]探索了二值化神经网络,其权值为- 1/1或-1/0/1。
- Han等人使用剪枝,量化和霍夫曼编码的方式达到了更高的压缩比例。
- 此外,Wang 等人将离散度的cos变换引入(discrete cosine transform(DCT)),将卷积核转到频域内进行运算,从而得到压缩率更高的模型和更大的速度提升
- 随后,Wang等人将 CNN 的 feature map 在频域上进行压缩,直接加速了卷积的计算
- Sun 等人引入最小绝对收缩(least absolute shrinkage)和选择算子(selection operation)设计了一种高效网络的选择方法
- Wang 等人提出了一种新的基于Group-Lasso的剪枝算法,具有较好的泛化性和剪枝效率。
- Huang 和 Yu 在训练时通过低秩近似的方式将权重矩阵 reshape 成高维张量来实现权重矩阵的压缩。
虽然上述的算法在 CNN 的压缩方面达到了令人满意的效果,但是通过这些压缩算法得到的网络结构与原来的网络结构有着非常大的差异,也就是说,这意味着高速推理需要特殊的实现,从而增加了开发成本。
Layer Decomposition
一些工作试图设计轻量级的网络层,从而实现高效的网络。
- Jin 等人提出了 fully factorized convolution(完全分解卷积)来加速神经网络的前馈过程
- Wang 等人通过考虑空间卷积(spatial convolution)的方式来分解卷积层(factorize convolution)
- SqueezeNet 利用 bottleneck 的架构,达到了和 AlexNet 同样的精度,但是只用了 少于1/50的参数。
- Pang等人提出了sparse-shallow MLP 来构建深层网络,达到了更少的参数和更高精确度的目标
- 因为 CNN 中涉及的卷积运算是非常耗时的,很多算法尝试重新设计卷积层。
- MobileNets 引入了 depth-wise separable convolution (深度可分卷积),从而很大程度上减少了卷积层的运算开销
- ShuffleNet 结合了 pointwise group convolution ( Group Convolution + Depthwise Separable Convolution)和 channel shuffle 来减少运算复杂度,但仍能保证很高的 accuracy
- Wu 等人提出了一个 parameter-free(无参数) “变换”操作,来替普通卷积
- 还有很多,例如 Sandler等人通过引入一个反向的残差结构(inverted residual structure)提升 MobileNets,这个结构也包含了 linear bottleneck 层
- Ma 等人提出了一个超越FLOPs的新指标来衡量CNNs速度;这导致了 ShuffleNet V2 的出现。
- 与设计低运算开销的卷积层方法不同,Wang等[43]利用通用的 filter 的方法实现了CNNs中滤波器的重复使用,取得了较好的性能。
Knowledge Distillation
与直接压缩重网络不同,一些研究通过研究原始网络的内在信息来学习产生较小的网络
- 知识迁移(knowledge transfer),最早由 Hinton 等人开创。[19],旨在:当学生网络的参数较少时,通过借鉴另一个强大的教师网络的知识来指导学生网络的训练。
- 它使用教师网络最终输出的 logits 为 soft target 来指导学生网络训练。除了 logits 输出层之外,教师网络的中间层特征(intermediate layers)还包含着对学生网络学习具有指导作用的有用信息
- 因此, Romero[21]将学生网络中的 hint layer 与教师网络中的 guide layer 的特征差异最小化,使学生网络能够从教师网络接收到足够的信息。
- McClure和Kriegeskorte[20]提出了成对样本之间的距离(pairwise distance of samples)作为有用的知识来完成知识迁移过程,从而提高了学生网络的鲁棒性。
- 从集成学习算法获得启发(ensemble learning methods),You 等人同时利用多个教师网络来共同指导一个学生网络的学习。此外,还开发了几种算法来研究教师与学生之间的约束
- Zagoruyk和Komodakis[24]利用了注意力机制(attention mechanism),并提出转移注意力地图(attention maps),这可以看作是全激活的总结。
- Huang和Wang[25]将知识转移作为一个分布匹配问题(distribution matching),利用最大平均差异(Maximum Mean difference, MMD) 指标 来最小化 teacher 和 student 特征之间的差异
- Wang 等人利用生成式对抗网络,使师生网络的特征分布相似。
- 与网络修剪(network trimming)方法相比,teacher-student 模型可应用于主流硬件,无需特殊要求,且易于与层分解方法相结合。
- 现有的知识蒸馏算法可以在教师网络的指导下学习高效的网络。然而,这些方法通常利用全连接层来弥补教师网络的高维特征和学生网络的低维特征之间的差距,从而引入了大量的附加参数。
- 例如,需要一个 19 G B 19GB 19GB参数容量的全连接层来连接教师网络(如ResNet-101)中的 7 × 7 × 2048 7×7×2048 7×7×2048 维的中间特征和学生网络(如Inception-BN)中的 7 × 7 × 2048 7×7×2048 7×7×2048 维的中间特征。
- 考虑到这些巨大的空间和计算复杂性,迫切需要一种灵活有效的算法来在教师和学生的特征之间传递知识
STUDENT NETWORK EMBEDDING
Teacher-student Interactions
-
为了实现便携式架构,Hinton等人[19]首先提出了知识蒸馏(KD)方法,该方法利用教师网络的软化输出(soft target)将信息迁移到较小的学生网络中。
-
Clure和Kriegeskorte[20]进一步提出了在之前 KD 的基础上,对学生网络和教师网络训练之后,再最小化样本的两两距离(pairwise distance of samples)。
-
N T N_T NT 和 N S N_S NS 分别代表原始的 pre-trained 的卷积神经网络(teacher)和需要被训练的轻便网络(student)
-
KD 的目标是利用 N T N_T NT 去提升 N S N_S NS 的表现
-
把 teacher 网络 N T N_T NT 的 softmax 的输出记作: P T = s o f t m a x ( a T ) P_T = softmax(a_T) PT=softmax(aT)
- a T a_T aT 代表的是输入激活层的 logits 结果
-
同样地 P S = s o f t m a x ( a S ) P_S = softmax(a_S) PS=softmax(aS) 代表 student 网络的 softmax 只后的概率输出
- a S a_S aS 代表的是输入激活层的 logits 结果
-
比较原来数据集中的 one-hot label,这个 output 可以转移更多的 teacher 的信息。因为其中包含了很多不同类之间的信息。
-
通过损失函数的方式来不断逼近 teacher 和 student 网络的 soften outputs,student 网络就可以继承更多丰富的 teacher 网络的有用信息;student 网络借助学习的 loss function 定义为:
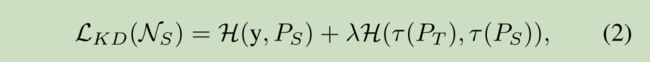
- 其中 H H H 是 cross-entropy loss,
- y y y 是 ground-truth 标签,
- λ λ λ 表示的是一个超参数,用来平衡第一项和第二项的比重
- 第一部分表示的是 ground-truth 与 student 的 soft output 之间的误差
-
但是由于 teacher 网络和 student 之间参数容量和结构的巨大差异,导致:仅通过最后一层 logits 来约束和指导 student 的学习过程并不容易实现
-
另外,我们已知在 teacher 网络的中间层特征也包含了大量有用的信息
-
Romero 等人 提出了一种更加灵活的 FitNet 方法,通过引入中间隐藏层来连接教师和学生网络,比传统的 KD 网络模型的精确度表现好很多
-
FitNet 分为根据 teacher-student 的范式分为两个步骤来训练。
-
具体来讲:
1) 在 student 网络中的 guided layer(对应teacher网络的 hint layer) 之后添加一个全连接网络。 f S f_S fS 和 f T f_T fT 分别代表 student 的 guided 层生成的 feature 和 teacher 的 hint 层生成的 feature。第一阶段的损失函数公式如下:

- 为了使 student 中 guided 层的输出匹配 teacher 中 hint 层输出特征的维度,使用 r r r 来表示这个加在 student 的 guided 层后的全连接层
2) student 网络 N S N_S NS 被按照 (公式2)中所示的方式进行约束;这是第二阶段的任务
因为中间的 hint 层的特征维度远远高于最后 softmax 层输出的维度,因此,FitNet可以从 teacher-student 中间层的特征中转移更多的有用信息,并由此生成一个更高精度的 student 网络
-
除此之外,也有许多研究提出通过引入不同的假设来进一步提高学生网络的精度。
- Yim 等人通过引入FSP(求解流程)矩阵来传递卷积层之间的关系。
- You 等人同时利用多个教师网络为了进一步提高学生网络的精度。
- Zagoruyko 等人[24]通过注意力图(attention maps)从教师网络中传递有用的信息
- Huang等人将知识转移作为一个分布匹配问题(distribution matching),利用最大平均差异(Maximum Mean difference, MMD) 指标 来最小化 teacher 和 student 特征之间的差异
- Wang 等人利用生成式对抗网络,使师生网络的特征分布相似。
-
然而,这里仍然有需要被解决的问题:
1) 公式3 只是片面单独地考虑了他们单个的数据点,并没有探索他们之间的联系
2) 引入的 全连接 r r r 增加了计算的复杂度
Locality Preserving Loss
-
如上所述,学生网络的特征维度低于教师网络的特征维度
-
我们提出将 student 网络的学习看作是一种低维的嵌入过程(low-dimensional embedding),旨在学习高效的低维度特征
-
考虑到无论在高维空间还是在低维空间,输入内容相似的图像都应该位于相邻区域,我们提出利用流形学习方法(manifold learning approach)来解决 teacher-student 的学习范式问题。
-
为了获得精确的低维表示法,人们提出了许多非线性流形学习方法。
- 局部线性嵌入(LLE[44]) 试图通过 将每个输入点重构为其相邻点的加权组合 来局部表示流形
- Isomap[45]通过返回一个embedding 来保持几何距离;这个 embedding 不同点之间的距离近似等于最短路径的距离;而拉普拉斯特征图(laplacian eigenmaps)建立一个包含数据集的邻域信息的图来计算数据集的低维表示,该数据集在某种意义上最优地保留了本地邻域信息。
-
然而,由于计算和存储资源的巨大开销,这些非线性方法并不适用于大规模问题。
-
相比之下,locality perserving projection (LPP[47])是对这些非线性方法的一种线性替代,可以很容易地嵌入到卷积神经网络的学习中。
-
具体来说,给定一个标注好的 training set,其中:
- 有 n n n 个样本, { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } \{(x^1,y^1),(x^2,y^2),...,(x^n,y^n)\} {(x1,y1),(x2,y2),...,(xn,yn)},
- 我们把 从 teacher 和 student 中提取出来的样本 x i x^i xi 的特征分别表示为: f T i f_T^i fTi 和 f S i f_S^i fSi;
-
因此,我们提出像保留教师网络一样保留学生网络生成的特征的局部关系,可以表示为:

- W S W_S WS 是 student 网络在 guided 层之前的参数;
- α i , j α_{i,j} αi,j 描述了 teacher 中 hint 层产生的 f e a t u r e ( i ) feature(i) feature(i)与 f e a t u r e ( j ) feature(j) feature(j)之间的关系
- 特别地, α i , j α_{i,j} αi,j 可以被定义如下:
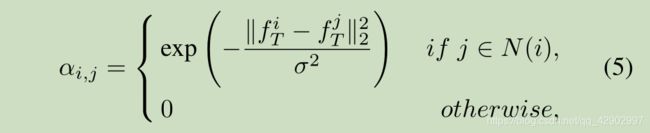
- N ( i ) N(i) N(i) 表示教师网络生成的第 i i i 幅图像 x i x^i xi 的特征 f T i f^i_T fTi 的 k k k 个最近邻
- σ \sigma σ 是一个标准化常数
-
通过优化Eq. 4,我们可以得到一个学生网络 N S N_S NS,这个学生网络保留了高维空间样本与目标低维空间样本之间关系(preserving relationship)
-
但是,为了计算 k k k 个最近邻,我们需要在每次迭代中取整个训练集,这是低效的。
-
因此,我们使用 mini-batch 策略来训练学生网络, k k k 个最近的邻居只会在 mini-batch 中通过计算获取。
-
此外,ground-truth 标签数据也被用于帮助学生网络的训练过程。所提网络的整个目标函数可表示为:
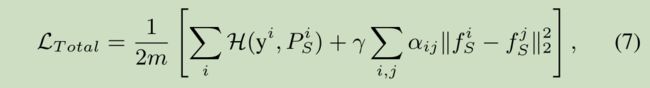
- γ \gamma γ 是权重参数,为了平衡前后两项的比重
- P S i P_S^i PSi 是学生网络在数据集的第 i i i 个 sample x i x^i xi 上的分类器的输出结果
- 公式7 的第一部分的任务是最小化分类器的 cross-entropy 来保持 student 网络的表现
- 公式7 的第二部分将 sample 从高维空间嵌入低维空间的 student 网络 N S N_S NS
- 而且, 我们还可以和 公式2 中的 KD loss 结合起来,共同提高模型的表现,使得 student 网络可以获得更多的信息
-
- 我们使用 SGD(stochastic gradient descent 随机梯度下降) 方法来优化学生网络
- 因为 LP loss 是一个线性的操作, L L P L_{LP} LLP 关于 f S i f_S^i fSi 的梯度可以被如下公式计算:

- 公式8 中的第一部分,就是那个分类误差函数,将会影响 student 网络中的参数,所以 N S N_S NS 中 guided 层之前的那些参数可以使用如下公式来进行参数更新:

- ∂ f S i ∂ W S \frac{\partial f_S^i}{\partial W_S} ∂WS∂fSi 是特征 f S i f_S^i fSi 的梯度;