nn.BatchNorm2d原理探究与实验

前言

早上被同学为了batch norm的原理，由于我之前仅仅停留在使用torch.nn.BatchNorm2d的阶段，只知道是对channel维度就行批归一化，但不太清楚具体实现，于是就做了该实验。先来看看torch的例子，然后再写个手写版方式计算的代码。
bn的后的每一个元素 $y_i$ 可简单写为
$$y_i=\frac{x_i-\bar{x}}{\sqrt{{\sigma }^2}+ϵ}$$
其中， $x_i$ 是之前的元素， $\bar{x}$ 是channel维度上的均值， $\sigma$ 是channel 维度上的标准差, $ϵ$ 是一个系数因子， (有点类似于拉普拉斯平滑，防止分母为0?but I’m not sure), 默认为$10^{-5}$, 很小的一个数。


另外Batch Norm用的多还是在CV， NLP用的少(NLP LayerNorm用的多)，所以就以CV中的图片为例子。
关于各种Norm可见一篇推送 综述：神经网络中 Normalization 的发展历程 。

torch方式

[B, C, H, W]分别指的是batch_size, channel(彩色图为三，灰色图为1，本例子只是为了方便演示，只有2维，大家知道就好)，图片的宽和高。

# encoding:utf-8
import torch
import torch.nn as nn


# [B, C, H, W]
input = torch.tensor([[[[1, 1],
                        [1, 2]],
                       [[-1, 1],
                        [0, 1]]],
                      [[[0, -1],
                        [2, 2]],
                       [[0, -1],
                        [3, 1]]]]).float()


# num_features - num_features from an expected input of size:batch_size*num_features*height*width
# eps:default:1e-5 (公式中为数值稳定性加到分母上的值)
# momentum:动量参数，用于running_mean and running_var计算的值，default：0.1
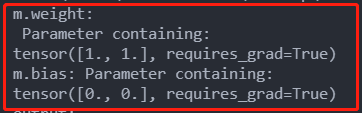
# affine参数设为True表示weight和bias将被使用, 不过该例子中没有反向传播, 所以加不加都是无所谓的
m = nn.BatchNorm2d(2, affine=False)
output = m(input)

# print('input:\n', input)
print('m.weight:\n', m.weight)
print('m.bias:', m.bias)
print('output:\n', output)
print('output:', output.size())

这里要说明的是, 其实不管affine设不设置为True，在该例子中结果都一样，我们看一下权重就明白了, weight全1， 那么进行相乘后还为原来的数， bias为0， 那么相加后还为原来的数。这里没有反向传播，所以权重不会变。

手写方式

我们除了channel通道外，其他维度都给展平， 然后去算均值和方差，用算出来的均值和方差再对原来的数据进行操作。

# encoding:utf-8
from matplotlib.pyplot import axis
import torch
import torch.nn as nn


input = torch.tensor([[[[1, 1],
                        [1, 2]],
                       [[-1, 1],
                        [0, 1]]],
                      [[[0, -1],
                        [2, 2]],
                       [[0, -1],
                        [3, 1]]]]).float()

# [B, C, H, W]
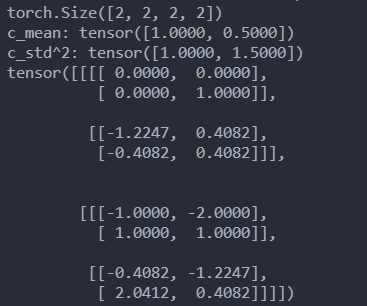
N, c_num, h, w = input.shape
print(input.shape)

x = input.transpose(0, 1).flatten(1)
# print(x)

c_mean = x.mean(dim=1)
print('c_mean:', c_mean)  
c_std = torch.tensor(x.numpy().std(axis=1))   # 标准差公式, torch N-1, numpy N
print('c_std^2:', c_std ** 2)    

# # 扩大维度，并复制好元素，方便下面批次操作
c_mean = c_mean.reshape(1, 2, 1, 1).repeat(N, 1, h, w)
c_std = c_std.reshape(1, 2, 1, 1).repeat(N, 1, h, w)
# # print(c_mean)
# # print(c_std)

eps = 1e-5
output = (input - c_mean) / (c_std ** 2 + eps) ** 0.5
print(output)

这里需要注意一下， pytorch和numpy的标准差计算公式是有区别的， 所以我代码中才先转为了numpy再去算。不过按理pytorch应该可以传个参数啥的去改一下计算方式吧。
numpy:
$$std=\sqrt{\frac{1}{N}\sum _{i=1}^N(x_i-\bar{x}{)}^2}$$

torch:
$$std=\sqrt{\frac{1}{N-1}\sum _{i=1}^N(x_i-\bar{x}{)}^2}$$