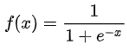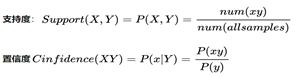关于机器学习数据挖掘的算法总结(优缺点)
目录
一、支持向量机(SVM)
二、朴素贝叶斯
三、逻辑回归Logistic Regression
四、线性回归
五、最近领算法——KNN
六、决策树
七、K-Means聚类
八、层次聚类
九、DBSCAN的分析
十、回归(Regression)算法
十一、聚类算法(Clustering Algorithms)
十二、贝叶斯公式
十三、Apriori算法
一、支持向量机(SVM)
SVM:中文名叫支持向量机,它的基本模型是定义在特征空间上的间隔最大的线性分类器。具体来说就是在线性可分时,在原空间寻找两类样本的最优分类超平面。在线性不可分时,加入松弛变量并通过非线性映射将低维输入空间的样本映射到高维空间使其变为线性可分,这样就可以在该特征空间中寻找最优分类超平面。
主要思想为找到空间中的一个更够将所有数据样本划开的超平面,并且使得本本集中所有数据到这个超平面的距离最短。
原理:找到离分隔超平面最近的点,确保它们离分隔平面的距离尽可能远
优点
- 可以解决高维问题,即大型特征空间;
- 解决小样本下机器学习问题;
- 能够处理非线性特征的相互作用;
- 无局部极小值问题;(相对于神经网络等算法)
- 无需依赖整个数据;
- 泛化能力比较强;
缺点
- 当观测样本很多时,效率并不是很高;
- 对非线性问题没有通用解决方案,有时候很难找到一个合适的核函数;
- 对于核函数的高维映射解释力不强,尤其是径向基函数;
- 常规SVM只支持二分类;
- 对缺失数据敏感;
二、朴素贝叶斯
朴素贝叶斯属于生成式模型(关于生成模型和判别式模型,主要还是在于是否是要求联合分布),非常简单,你只是做了一堆计数。如果注有条件独立性假设(一个比较严格的条件),朴素贝叶斯分类器的收敛速度将快于判别模型,如逻辑回归,所以你只需要较少的训练数据即可。即使NB条件独立假设不成立,NB分类器在实践中仍然表现的很出色。它的主要缺点是它不能学习特征间的相互作用,用mRMR中R来讲,就是特征冗余。引用一个比较经典的例子,比如,虽然你喜欢Brad Pitt和Tom Cruise的电影,但是它不能学习出你不喜欢他们在一起演的电影。
优点:
- 朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练;
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点:
- 需要计算先验概率;
- 分类决策存在错误率;
- 对输入数据的表达形式很敏感。
三、逻辑回归Logistic Regression
属于判别式模型,有很多正则化模型的方法(L0, L1,L2,etc),而且你不必像在用朴素贝叶斯那样担心你的特征是否相关。与决策树与SVM机相比,你还会得到一个不错的概率解释,你甚至可以轻松地利用新数据来更新模型(使用在线梯度下降算法,online gradient descent)。如果你需要一个概率架构(比如,简单地调节分类阈值,指明不确定性,或者是要获得置信区间),或者你希望以后将更多的训练数据快速整合到模型中去,那么使用它吧。
优点:
- 实现简单,广泛的应用于工业问题上;
- 分类时计算量非常小,速度很快,存储资源低;
- 便利的观测样本概率分数;
- 对逻辑回归而言,多重共线性并不是问题,它可以结合L2正则化来解决该问题;
缺点:
- 当特征空间很大时,逻辑回归的性能不是很好;
- 容易欠拟合,一般准确度不太高
- 不能很好地处理大量多类特征或变量;
- 只能处理两分类问题(在此基础上衍生出来的softmax可以用于多分类),且必须线性可分;
- 对于非线性特征,需要进行转换;
四、线性回归
线性回归是用于回归的,而不像Logistic回归是用于分类,其基本思想是用梯度下降法对最小二乘法形式的误差函数进行优化,当然也可以用normal equation直接求得参数的解,结果为:![]() 而在LWLR(局部加权线性回归)中,参数的计算表达式为:
而在LWLR(局部加权线性回归)中,参数的计算表达式为: ![]() 由此可见LWLR与LR不同,LWLR是一个非参数模型,因为每次进行回归计算都要遍历训练样本至少一次。
由此可见LWLR与LR不同,LWLR是一个非参数模型,因为每次进行回归计算都要遍历训练样本至少一次。
优点: 实现简单,计算简单;
缺点: 不能拟合非线性数据.
五、最近领算法——KNN
KNN即最近邻算法,其主要过程为:
1. 计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等);
2. 对上面所有的距离值进行排序;
3. 选前k个最小距离的样本;
4. 根据这k个样本的标签进行投票,得到最后的分类类别;
如何选择一个最佳的K值,这取决于数据。一般情况下,在分类时较大的K值能够减小噪声的影响。但会使类别之间的界限变得模糊。一个较好的K值可通过各种启发式技术来获取,比如,交叉验证。另外噪声和非相关性特征向量的存在会使K近邻算法的准确性减小。
近邻算法具有较强的一致性结果。随着数据趋于无限,算法保证错误率不会超过贝叶斯算法错误率的两倍。对于一些好的K值,K近邻保证错误率不会超过贝叶斯理论误差率。
优点
- 理论成熟,思想简单,既可以用来做分类也可以用来做回归;
- 可用于非线性分类;天生支持多分类
- 训练时间复杂度为O(n);
- 对数据没有假设,准确度高,对outlier不敏感;
缺点
- 计算量大;当数据量比较大或者数据的特征比较多时,预测过程的时间效率太低
- 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
- 需要大量的内存;
六、决策树
决策树是一种可以用于分类与回归的机器学习算法,但主要用于分类。用于分类的决策树是一种描述对实例进行分类的树形结构。决策树由结点和边组成,其中结点分为内部结点和叶子结点,内部结点表示一个特征或者属性,叶子结点表示标签(脑回路图中黄色的是内部结点,蓝色的是叶子结点)。
优点
- 计算简单,易于理解,可解释性强;
- 比较适合处理有缺失属性的样本;
- 能够处理不相关的特征;
- 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
缺点
- 容易发生过拟合(随机森林可以很大程度上减少过拟合);
- 忽略了数据之间的相关性;
- 对于那些各类别样本数量不一致的数据,在决策树当中,信息增益的结果偏向于那些具有更多数值的特征(只要是使用了信息增益,都有这个缺点,如RF)。
七、K-Means聚类
K-means 算法是一个迭代优化算法,每次迭代我们需要重新计算簇的中心。一般就是通过计算每个簇类所有样本的平均值来获得。可以使用 Numpy 里面的 mean 方法np.mean(x,0)来计算均值。K-means是一类非常经典的无监督机器学习算法,通常在实际应用中用于从数据集中找出不同样本的聚集模式。其含义实际上就是对于每一个簇j,计算分配在其中的样本向量的平均值。
缺点
- 对数据类型要求较高,适合数值型数据;
- 可能收敛到局部最小值,在大规模数据上收敛较慢
- K值比较难以选取;
- 对初值的簇心值敏感,对于不同的初始值,可能会导致不同的聚类结果;
- 不适合于发现非凸面形状的簇,或者大小差别很大的簇。
- 对于”噪声”和孤立点数据敏感,少量的该类数据能够对平均值产生极大影响。
克服K-means的局限性
- 使用更大数量的簇
- 几个小的簇表示一个真实的 簇
- 使用基于密度的方法
八、层次聚类
优点:不需要提前假定聚类的簇数; 层次聚类结果可能对应着有意义的分类体系
(1)对于给定的样本集合,开始将每个样本分到一个类
(2)然后按照一定规则,例如类间距离最小,将最满足规则条件的两个类进行合并
(3)如此反复进行,每次减少一个类,直到满足停止条件,如所有样本聚为一类。
◼最小距离(MIN):将两个簇的数据点中距离最近的两个数据点间的距离作为这两个簇的距离
缺点:(1)容易受到极端值的影响;(2)单连接产生非常分散的簇,擅长处理非球形簇(3)对离群点和噪声敏感
◼最大距离(MAX):两个簇的数据点中距离最远的两个数据点间的距离作为这两个簇的距离
缺点:(1)全连接聚类并不能找出最直观的簇结构,容易打破大团(2)对离群点和噪声敏感
◼平均距离(Group Average):计算两个簇的数据点中的每个数据点与其他所有数据点的距离
优势:(1)MIN 和 MAX 的折中方案(2)该方法计算量比较大,但结果比前两种方法合理
(3)且对噪声和离群点没那么敏感
◼中心点距离 :计算方法是将两个簇的质心距离作为这两个簇的距离
优势:(1)减少组平均方法计算量比较大问题(2)对噪声和离群点没那么敏感(3)偏向于球型簇
九、DBSCAN的分析
DBSCAN算法原理
DBSCAN是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。
DBSCAN算法流程
在DBSCAN算法中,由核心对象出发,找到与该核心对象密度可达的所有样本形成一个聚类簇。
- 如果一个点的eps邻域包含多于MinPits个对象,则创建一个集合P作为核心对象的新簇。
- 寻找核心对象的直接密度可达的对象,并合并为一个新的簇。
- 直到没有点可以更新簇时算法结束。
优势
- 不需要明确簇的数量
- 任性形状的簇
- 对离群点(outliers)较为鲁棒性强(对噪声不敏感)
- 结果不应受到模型中存在的数据扰动、噪声及离群点的太大影响
劣势
- 参数选择比较困难(MinPts, ε)
- 不适合密度差异较大的数据集
- 需计算每个样本的邻居点,操作耗时(ON2);即使采用k-d tree索引等技术加速计算,算法的时间复杂也为ONlogN。
十、回归(Regression)算法
回归是用于估计两种变量之间关系的统计过程。当用于分析因变量和一个 多个自变量之间的关系时,该算法能提供很多建模和分析多个变量的技巧。具体一点说,回归分析可以帮助我们理解当任意一个自变量变化,另一个自变量不变时,因变量变化的典型值。最常见的是,回归分析能在给定自变量的条件下估计出因变量的条件期望。
回归算法是统计学中的主要算法,它已被纳入统计机器学习。
优点:
- 直接、快速
- 知名度高
缺点:
- 要求严格的假设
- 需要处理异常值
十一、聚类算法(Clustering Algorithms)
聚类算法是指对一组目标进行分类,属于同一组(亦即一个类,cluster)的目标被划分在一组中,与其他组目标相比,同一组目标更加彼此相似(在某种意义上)。
优点:让数据变得有意义
缺点:结果难以解读,针对不寻常的数据组,结果可能无用。
十二、贝叶斯公式
当已知引发事件发生的各种原因的概率,想要算该事件发生的概率时,我们可以用全概率公式。但如果现在反过来,已知事件已经发生了,但想要计算引发该事件的各种原因的概率时,我们就需要用到贝叶斯公式了。
贝叶斯公式定义如下,其中A表示已经发生的事件,Bi为导致事件A发生的第i个原因: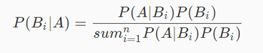
贝叶斯公式看起来比较复杂,其实非常简单,分子部分是乘法定理,分母部分是全概率公式(分母等于P(A))。
如果我们对贝叶斯公式进行一个简单的数学变换(两边同时乘以分母,再两边同时除以P(Bi))。就能够得到如下公式:
这个公式是朴素贝叶斯分类算法的核心数学公式
十三、Apriori算法
Apriori是一种常用的数据关联规则挖掘方法,它可以用来找出数据集中频繁出现的数据集合。找出这样的一些频繁集合有利于决策,例如通过找出超市购物车数据的频繁项集,可以更好地设计货架的摆放。需要注意的是它是一种逐层迭代的方法,先找出频繁1项集L1,再利用L1找出频繁2项集,以此类推……
关联规则:关联规则是形如 X→Y 的蕴涵表达式,其中X和Y是不相交的项集,即 X∩Y=∅。关联规则的强度可以用它的支持度(support)和置信度(confidence)来度量。
持续更新.....
♥♥♥每天提醒自己,自己就是个菜鸡!
♥♥♥已经看到最后啦,如果对您有帮助留下的每一个点赞、收藏、关注是对菜鸡创作的最大鼓励❀
♥♥♥有相关问题可以写在评论区,一起学习,一起进步。