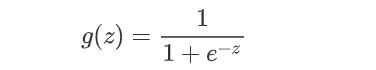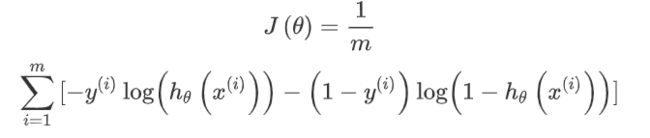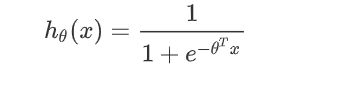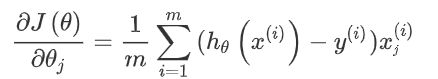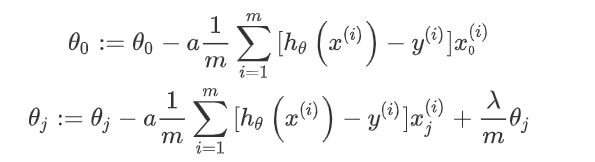吴恩达机器学习ex2 python实现

这个项目包含了吴恩达机器学习ex2的python实现，主要知识点为逻辑回归、正则化。

1.逻辑回归

构建一个逻辑回归模型来预测，某个学生是否被大学录取。对于每一个训练样本，你有他们两次测试的评分和最后是被录取的结果。

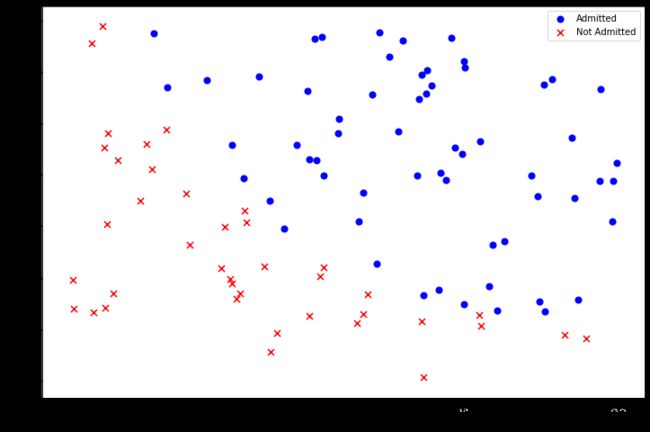
1.1查看数据分布

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path=r'C:\Users\xxx\Desktop\机器学习\machine-learning-ex2\machine-learning-ex2\ex2\ex2data1.txt'
data=pd.read_csv(path,header=None,names=['Exam 1','Exam 2','Admitted'])
data.head()

	Exam 1	Exam 2	Admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

1.2定义各种函数

定义sigmoid函数

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

定义代价函数

假设函数

def cost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    return np.sum(first - second) / (len(X))

定义梯度下降

def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        grad[i] = np.sum(term) / len(X)
    
    return grad

1.3数据预处理

data.insert(0, 'Ones', 1)

# 初始化X，y，θ
cols = data.shape[1]
X = data.iloc[:,:-1]
y = data.iloc[:,cols-1:cols]
theta = np.zeros(3)

# 转换X，y的类型
X = np.array(X.values)
y = np.array(y.values)

X.shape, theta.shape, y.shape

((100, 3), (3,), (100, 1))

1.4利用模型进行预测

cost(theta, X, y)

0.6931471805599453

调用库函数实现梯度下降

import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
result

(array([-25.16131872,   0.20623159,   0.20147149]), 36, 0)

cost(result[0],X,y)

0.20349770158947425

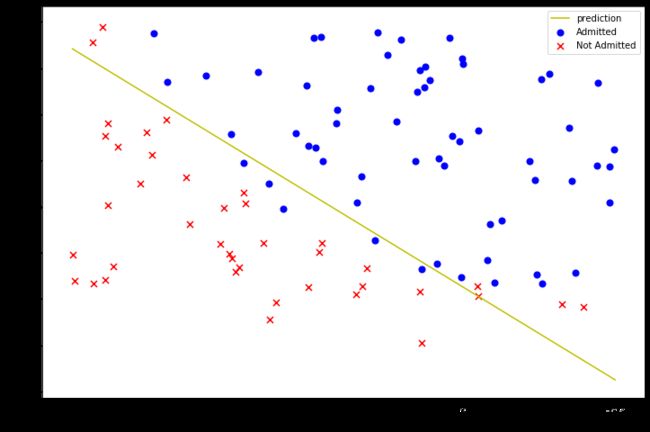
1.5画出决策曲线

plotting_x1 =np.linspace(30,100,100)
plotting_h1 =(-result[0][0]-result[0][1]*plotting_x1)/result[0][2]
# θ0+θ1x+θ2y=0
fig,ax= plt.subplots(figsize=(12,8))
ax.plot(plotting_x1,plotting_h1,'y',label='prediction')
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

1.5计算acc

def hfunc1(theta,X):
    return sigmoid(np.sum(X*theta))
hfunc1(result[0],[1,45,85])

0.776290625526598

def predict(theta,X):
    probability =sigmoid(X*theta.T)
    return [1 if x>=0.5 else 0 for x in probability]

theta_min=np.matrix(result[0])
predictions=predict(theta_min,X)
correct=[1 if((a==1 and b==1)or (a==0 and b==0))
         else 0 for(a,b)in zip(predictions,y)]
# print(sum(map(int ,correct)))
# print(len(correct))
acc=(sum(map(int ,correct))/len(correct)*100)
print('acc={0}%'.format(acc))

acc=89.0%

2.正则化逻辑回归

本项目在逻辑回归的基础上加入了正则化项

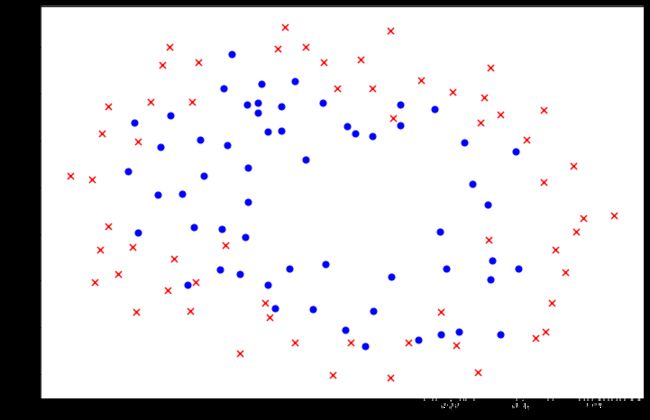
2.1查看数据分布

path=r'C:\Users\xxx\Desktop\机器学习\machine-learning-ex2\machine-learning-ex2\ex2\ex2data2.txt'
data_init=pd.read_csv(path,header=None,names=['Test 1', 'Test 2', 'Accepted'])
data_init.head()

	Test 1	Test 2	Accepted
0	0.051267	0.69956	1
1	-0.092742	0.68494	1
2	-0.213710	0.69225	1
3	-0.375000	0.50219	1
4	-0.513250	0.46564	1

postive2=data_init[data_init['Accepted'].isin([1])]
negative2=data_init[data_init['Accepted'].isin([0])]

fig,ax=plt.subplots(figsize=(12,8))
ax.scatter(postive2['Test 1'],postive2['Test 2'],s=50,c='b',marker='o',label='Accepted')
ax.scatter(negative2['Test 1'],negative2['Test 2'],s=50,c='r',marker='x',label=' Not Accepted')

2.2添加更多的特征

degree=6
data2=data_init
x1=data2['Test 1']
x2=data2['Test 2']
data2.insert(3,'Ones',1)
for i in range(1,degree+1):
    for j in range(0,i+1):
        data2['F'+str(i-j)+str(j)]=np.power(x1,i-j)*np.power(x2,j)
        
data2.drop('Test 1',axis=1,inplace=True)
data2.drop('Test 2',axis=1,inplace=True)
data2.head()

	Accepted	Ones	F10	F01	F20	F11	F02	F30	F21	F12	...	F23	F14	F05	F60	F51	F42	F33	F24	F15	F06
0	1	1	0.051267	0.69956	0.002628	0.035864	0.489384	0.000135	0.001839	0.025089	...	0.000900	0.012278	0.167542	1.815630e-08	2.477505e-07	0.000003	0.000046	0.000629	0.008589	0.117206
1	1	1	-0.092742	0.68494	0.008601	-0.063523	0.469143	-0.000798	0.005891	-0.043509	...	0.002764	-0.020412	0.150752	6.362953e-07	-4.699318e-06	0.000035	-0.000256	0.001893	-0.013981	0.103256
2	1	1	-0.213710	0.69225	0.045672	-0.147941	0.479210	-0.009761	0.031616	-0.102412	...	0.015151	-0.049077	0.158970	9.526844e-05	-3.085938e-04	0.001000	-0.003238	0.010488	-0.033973	0.110047
3	1	1	-0.375000	0.50219	0.140625	-0.188321	0.252195	-0.052734	0.070620	-0.094573	...	0.017810	-0.023851	0.031940	2.780914e-03	-3.724126e-03	0.004987	-0.006679	0.008944	-0.011978	0.016040
4	1	1	-0.513250	0.46564	0.263426	-0.238990	0.216821	-0.135203	0.122661	-0.111283	...	0.026596	-0.024128	0.021890	1.827990e-02	-1.658422e-02	0.015046	-0.013650	0.012384	-0.011235	0.010193

5 rows × 29 columns

2.2定义代价函数和梯度

代价函数

def costReg(theta,X,y,learningRate):
    theta=np.matrix(theta)
    X=np.matrix(X)
    y=np.matrix(y)
    first=np.multiply(-y,np.log(sigmoid(X*theta.T)))
    second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))
    reg=(learningRate/(2*len(X)))*np.sum(np.power(theta[:,1:],2))
    return np.sum(first-second)/len(X)+reg

梯度，分theta是否等于0

def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    return grad

2.3处理数据格式

cols=data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]
theta2 = np.zeros(cols-1)

X2=np.array(X2.values)
y2=np.array(y2.values)

learningRate=1

2.4 利用库进行预测

costReg(theta2,X2,y2,learningRate)

0.6931471805599454

result2=opt.fmin_tnc(func=costReg,x0=theta2,fprime=gradientReg, args=(X2, y2, learningRate))
result2

(array([ 1.27271027,  0.62529965,  1.18111686, -2.01987399, -0.91743189,
        -1.43166929,  0.12393228, -0.36553118, -0.35725403, -0.17516291,
        -1.45817009, -0.05098418, -0.61558554, -0.27469165, -1.19271298,
        -0.24217841, -0.20603298, -0.04466178, -0.27778951, -0.29539513,
        -0.45645981, -1.04319155,  0.02779373, -0.2924487 ,  0.0155576 ,
        -0.32742405, -0.1438915 , -0.92467487]), 32, 1)

theta_min = np.matrix(result2[0])
predictions = predict(theta_min, X2)
correct = [1 if ((a == b)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) /len(correct))*100
print(sum(map(int, correct)))
print ('accuracy = {0}%'.format(accuracy))

98
accuracy = 83.05084745762711%

2.4 决策曲线

def hfunc2(theta, x1, x2):
    temp = theta[0][0]
    place = 0
    for i in range(1, degree+1):
        for j in range(0, i+1):
            temp+= np.power(x1, i-j) * np.power(x2, j) * theta[0][place+1]
            place+=1
    return temp
    

def find_decision_boundary(theta):
    t1=np.linspace(-1,1.5,1000)
    t2=np.linspace(-1,1.5,1000)
    cordinates=[(x,y)for x in t1 for y in t2]
    x_cord,y_cord=zip(*cordinates)
    h_val=pd.DataFrame({'x1':x_cord,'x2':y_cord})
    h_val['hval']=hfunc2(theta, h_val['x1'], h_val['x2'])
#     print(h_val)
    decison=h_val[np.abs(sigmoid(h_val['hval'])-0.5)<0.01]
    return decison.x1,decison.x2

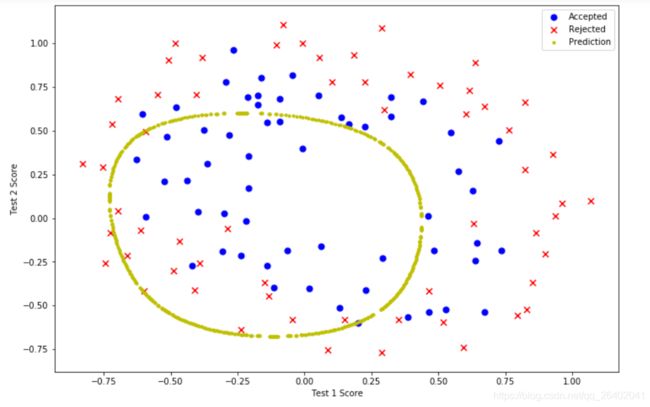
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(postive2['Test 1'], postive2['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative2['Test 1'], negative2['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')

x, y = find_decision_boundary(result2)
plt.scatter(x, y, c='y', s=10, label='Prediction')
ax.legend()
plt.show()

λ=100，欠拟合

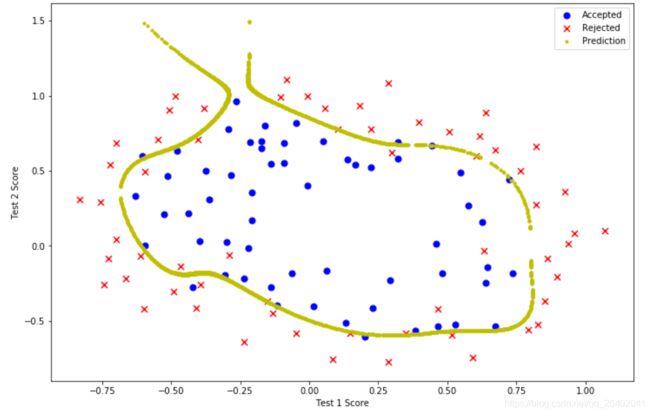
λ=0，过拟合

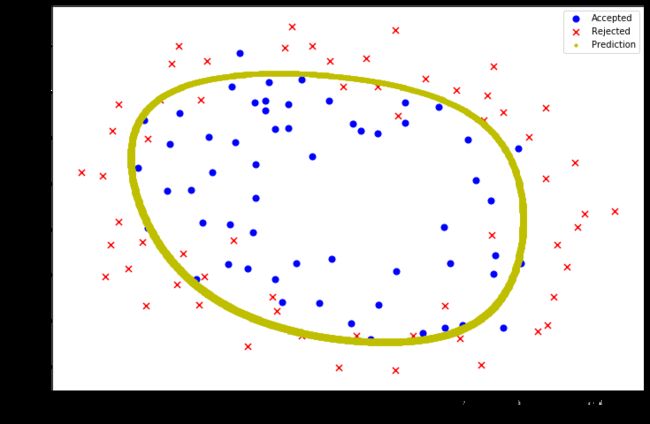
λ=1，拟合得比较好

总结

1. theta0不需要正则化
2. zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。zip() 和 * 操作符一起操作可以用来 unzip 一个列表