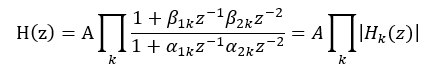实验(4)IIR数字滤波器的设计及结构
本文的pdf文件:link
一、实验目的
设计计算机程序,根据滤波器的主要技术指标设计IIR数字巴特沃斯和切比雪夫低通,高通,带通和带阻滤波器;绘制滤波器的幅频特性和相频特性曲线,验证滤波器的设计结果是否达到设计指标要求;画出数字滤波器的直接型,级联型,并联型结构信号流图。
二、实验原理
2.1 数字滤波器
指输入输出均为数字信号,通过一定运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分的器件。因为数字滤波器通过数值运算实现滤波,所以数字滤波器具有如下优点:精度高、稳定、体积小、重量轻、灵活、不要求阻抗匹配以及可实现模拟滤波器无法实现的特殊功能等。
从滤波特性上来说可分为低通、高通、带通、带阻和全通。其各自的幅频响应如下图所示:

2.2 巴特沃斯低通滤波器
2.2.1 巴特沃斯滤波器的特点
N阶巴特沃斯低通滤波器的幅度平方函数为:
∣ H a ( j Ω ) ∣ 2 = 1 / ( 1 + ( Ω / Ω c ) 2 N ) , Ω c 为 3 d B 截 止 频 率 |H_a (jΩ)|^2=1/(1+(Ω/Ω_c )^2N ) ,Ω_c 为3dB截止频率 ∣Ha(jΩ)∣2=1/(1+(Ω/Ωc)2N),Ωc为3dB截止频率
其幅频响应与阶数N的关系如下图所示:

2.2.2 巴特沃斯滤波器的设计步骤
1.根据技术指标 Ω p 、 α p 、 Ω s 和 α s Ω_p 、α_p 、Ω_s和α_s Ωp、αp、Ωs和αs,用(1)式求出滤波器的阶数N。
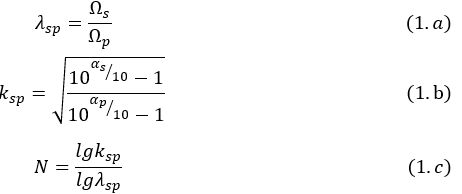
2.按照(2)式,求出归一化极点 p k p_k pk,将 p k p_k pk代入(3)式,得到归一化低通原型系统函数 G a ( p ) G_a (p) Ga(p)。也可以根据阶数N直接查表(教材P_172)得到 p k p_k pk和 G a ( p ) G_a (p) Ga(p)。
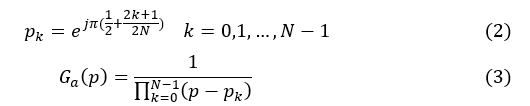
3.将 G a ( p ) G_a (p) Ga(p)去归一化。将 p = s / Ω c p=s/Ω_c p=s/Ωc代入 G a ( p ) G_a (p) Ga(p),得到实际的滤波器系统函数
H a ( s ) = G ( p ) ∣ ( p = s / Ω c ) H_a (s)=G(p)|(p=s/Ω_c ) Ha(s)=G(p)∣(p=s/Ωc)
2.3 切比雪夫Ι型低通滤波器
2.3.1 切比雪夫滤波器的特点
切比雪夫II型滤波器的平方幅度响应为:
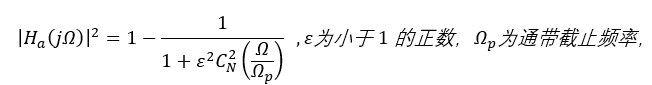
各自的幅频响应曲线如下图所示:
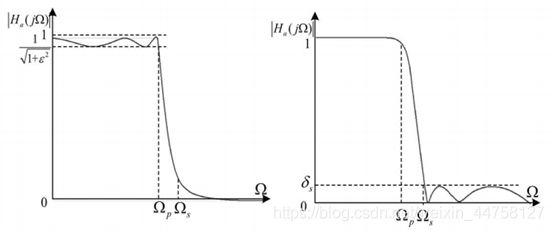
2.3.2 切比雪夫滤波器的设计步骤
1)确定技术指标参数 Ω p 、 α p 、 Ω s 和 α s Ω_p 、α_p 、Ω_s和α_s Ωp、αp、Ωs和αs。
2)求滤波器阶数N和参数ε。归一化边界频率为 λ p = 1 , λ s = Ω s ⁄ Ω p λ_p=1,λ_s=Ω_s⁄Ω_p λp=1,λs=Ωs⁄Ωp

其中

3)求归一化系统函数 G a ( p ) G_a (p) Ga(p)。为求 G a ( p ) G_a (p) Ga(p),先按照(4)式求出归一化极点 p k , k = 1 , 2 , … , N . p_k,k=1,2,…,N. pk,k=1,2,…,N.
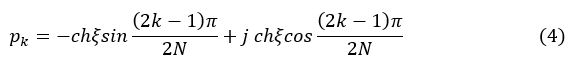
将极点 p k p_k pk代入式(5),得到:
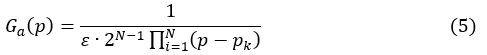
4)将 G a ( p ) G_a (p) Ga(p)去归一化,得到实际的 H a ( s ) H_a (s) Ha(s)
H a ( s ) = G a ( p ) ∣ ( p = s ⁄ Ω p ) H_a (s)=G_a (p)|(p=s⁄Ω_p ) Ha(s)=Ga(p)∣(p=s⁄Ωp)
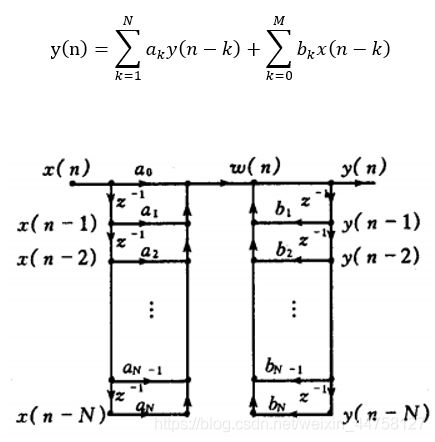
2.4 数字滤波器的直接型、级联型、并联型结构信号流图
2.4.1直接型
2.4.2级联型
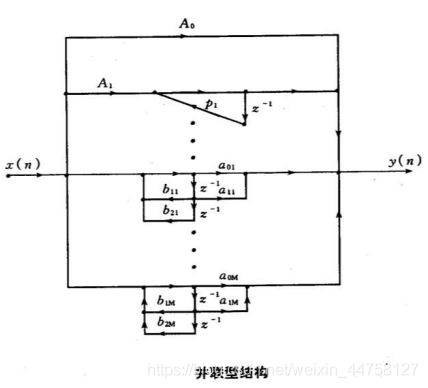
2.4.3并联型
三、实验总结
根据所要设计滤波器的响应指标就可以求得响应的滤波器参数,然后在进行频域转换得到数字滤波器。以下便是设计IIR滤波器的流程:

四、matlab代码
% 实验五:IIR数字滤波器设计及结构
% 设计计算机程序,根据滤波器的主要技术指标设计IIR数字巴特沃斯和切比雪夫低通,高通,带通和带阻滤波器;
% 绘制滤波器的幅频特性和相频特性曲线,验证滤波器的设计结果是否达到设计指标要求;
% 画出数字滤波器的直接型,级联型,并联型结构信号流图。
fs = 30;
Wp = 3;
Ws = 7;
Rp = 1;
Rs = 40;
[N,Wc]=buttord(Wp,Ws,Rp,Rs,'s');
[B,A]=butter(N,Wc,'low','s');
[Bz,Az] = impinvar(B,A,fs);
W=0:0.001:50;
[H,W]=freqs(B,A,W);
phi=angle(H);
H=20*log10(abs(H));
figure(1);
plot(W,H);
title('滤波器的幅频响应');
xlabel('w');
ylabel('|Hw|');
grid on;
figure(2)
plot(W,phi);
title('滤波器的相频响应');
xlabel('w');
ylabel('angle(Hw)');
grid on;
%巴特沃斯低通滤波器
fHp=1000;fHs=5000;
wp=2*pi*fHp;
ws=2*pi*fHs;
Rp=1;
Rs=10;
f=1:10:6000;
w=2*pi.*f;
[N,wc]=buttord(wp,ws,Rp,Rs,'s');
[b,a]=butter(N,wc,'low','s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(f,20*log10(abs(H)));
title('巴特沃斯低通滤波器幅频特性');
subplot(2,1,2);
plot(f/1000,angle(H));
title('巴特沃斯低通滤波器相频特性');
%巴特沃斯高通滤波器
fHp=5000;fHs=1000;
wp=2*pi*fHp;
ws=2*pi*fHs;
Rp=1;
Rs=10;
f=1:10:6000;
w=2*pi.*f;
[N,wc]=buttord(wp,ws,Rp,Rs,'s');
[b,a]=butter(N,wc,'high','s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(f/1000,20*log10(abs(H)));
title('巴特沃斯高通滤波器幅频特性');
subplot(2,1,2);
plot(f/1000,angle(H)*180/pi);
title('巴特沃斯高通滤波器相频特性');
%巴特沃斯带通滤波器
wp=[6,8];
ws=[4,11];
Rp=1;
Rs=40;
w=1:0.01:14;
[N,wc]=buttord(wp,ws,Rp,Rs,'s');
[b,a]=butter(N,wc,'s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(w,20*log10(abs(H)));
title('巴特沃斯带通滤波器幅频特性');
subplot(2,1,2);
plot(w,angle(H)/pi);
title('巴特沃斯带通滤波器相频特性');
%巴特沃斯带阻滤波器
fsl=980;
fsu=1020;
fpl=905;
fpu=1105;
wpl=2*pi*fpl;
wsl=2*pi*fsl;
wpu=2*pi*fpu;
wsu=2*pi*fsu;
wp=[wpl,wpu];
ws=[wsl,wsu];
Rp=3;
Rs=25;
f=1:1:1600;
w=2*pi.*f;
[N,wc]=buttord(wp,ws,Rp,Rs,'s');
[b,a]=butter(N,wc,'stop','s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(f/1000,20*log10(abs(H)));
title('巴特沃斯带阻滤波器幅频特性');
subplot(2,1,2);
plot(f/1000,angle(H)*180/pi);
title('巴特沃斯带阻滤波器相频特性');
%切比雪夫Ⅰ型低通滤波器
Rp=1;
Rs=40;
wp=0.5;
ws=0.7;
w=0.4:1/2000:1;
[N,Wpo]=cheb1ord(wp,ws,Rp,Rs);
[b,a]=cheby1(N,Rp,Wpo,'low','s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(w,20*log10(abs(H)));
title('切比雪夫低通滤波器幅频特性');
subplot(2,1,2);
plot(w,angle(H)*180/pi);
title('切比雪夫低通滤波器相频特性');
%切比雪夫Ⅰ型高通滤波器
Rp=1;
Rs=40;
wp=0.7;
ws=0.5;
w=0.4:1/2000:1;
[N,Wpo]=cheb1ord(wp,ws,Rp,Rs);
[b,a]=cheby1(N,Rp,Wpo,'high','s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(w,20*log10(abs(H)));
title('切比雪夫高通滤波器幅频特性');
subplot(2,1,2);
plot(w,angle(H)*180/pi);
title('切比雪夫高通滤波器相频特性');
%切比雪夫Ⅱ型带通滤波器
wpl=0.5062;
wpu=0.5563;
wsl=0.3750;
wsu=0.6750;
w=0.3:1/10000:0.8;
rp=1;
rs=40;
wp=[wpl,wpu];
ws=[wsl,wsu];
[N,wso]=cheb2ord(wp,ws,rp,rs,'s');
[b,a]=cheby2(N,rs,wso,'s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(w,20*log10(abs(H)));
title('切比雪夫带通滤波器幅频特性');
subplot(2,1,2);
plot(w,angle(H)*180/pi);
title('切比雪夫带通滤波器相频特性');
%切比雪夫Ⅱ型带阻滤波器
wsl=980;
wsu=1020;
wpl=905;
wpu=1105;
w=1:1:1600;
rp=3;
rs=25;
wp=[wpl,wpu];
ws=[wsl,wsu];
[N,wso]=cheb2ord(wp,ws,rp,rs,'s');
[b,a]=cheby2(N,rs,wso,'stop','s');
[H,wh]=freqs(b,a,w);
figure(1);
subplot(2,1,1);
plot(w,20*log10(abs(H)));
title('切比雪夫带阻滤波器幅频特性');
subplot(2,1,2);
plot(w,angle(H)*180/pi);
title('切比雪夫带阻滤波器相频特性');