【拉普拉斯机制代码实现demo】差分隐私代码实现系列(四)
差分隐私代码实现系列(四)
- 写在前面的话
- 回顾
- 差分隐私(Differential Privacy)
- 拉普拉斯机制(The Laplace Mechanism)
- 多少噪音就足够了?(How Much Noise is Enough?)
- 总结
写在前面的话
书上学来终觉浅,绝知此事要躬行。
回顾
1、 k k k-Anonymity是数据的一个属性,它确保每个个体都与至少一组 k k k个体"融合"。
2、 k k k-Anonymity甚至在计算上也很昂贵:朴素算法是 O ( n 2 ) O(n^2) O(n2),更快的算法占用相当大的空间。
3、 k k k-Anonymity可以通过泛化数据集来修改数据集来实现,这样特定值变得更加常见,组更容易形成。
4、最优泛化极其困难,异常值可能使其更具挑战性。自动解决这个问题是NP困难的。
好了,准备进入差分隐私!激动的心,颤抖的手~
差分隐私(Differential Privacy)
与 k k k-Anonymity一样,差分隐私是隐私的正式概念(即可以证明数据发布具有该属性)。
然而,与 k k k-Anonymity不同,差分隐私是算法的属性,而不是数据的属性。
也就是说,我们可以证明算法满足差分隐私。
为了证明数据集满足差分隐私,我们必须证明产生它的算法满足差分隐私。
定义:
满足差分隐私的函数通常称为机制。我们说,如果对于所有相邻数据集 x x x和 x ′ x' x′以及所有可能的输出 S S S,
P r [ F ( x ) = S ] P r [ F ( x ′ ) = S ] ≤ e ϵ \frac{\mathsf{Pr}[F(x) = S]}{\mathsf{Pr}[F(x') = S]} \leq e^\epsilon Pr[F(x′)=S]Pr[F(x)=S]≤eϵ
如果两个数据集中只存在单个个体的数据不同,则将其视为相邻数据集。
请注意, F F F通常是一个随机函数,因此描述其输出的概率分布不仅仅是点分布。
这个定义的重要含义是 F F F的输出将几乎相同,无论有没有任何特定个人的数据。
换句话说,内置于 F F F中的随机性应该是"足够的",以便从 F F F观察到的输出不会揭示 x x x或 x ′ x' x′中哪一个是输入。
想象一下,我的数据存在于 x x x中,但不存在于 x ′ x' x′中。如果对手无法确定 x x x或 x ′ x' x′中的哪一个是 F F F的输入,那么对手就无法判断输入中是否存在我的数据,更不用说该数据的内容了。
定义中的 ϵ \epsilon ϵ参数称为隐私参数或隐私预算。 ϵ \epsilon ϵ提供了一个旋钮来调整定义提供的"隐私量"。
当 ϵ \epsilon ϵ的值较小时,要求 F F F在给定相似的输入时提供非常相似的输出,因此提供更高级别的隐私;
当 ϵ \epsilon ϵ的值较大时,允许输出中的相似性降低,因此提供的隐私较少。
我们应该如何设置 ϵ \epsilon ϵ来防止在实践中出现不良后果?没有人知道。
普遍的共识是 ϵ \epsilon ϵ应该在1左右或更小,并且 ϵ \epsilon ϵ的值高于10可能对保护隐私没有多大作用 ,但这个经验法则可能会变得非常保守。
大家如果还想更进一步了解差分隐私可以去看看我的博客,或者看论文,概念性的介绍这里就不罗嗦了。
拉普拉斯机制(The Laplace Mechanism)
差分隐私通常用于回答特定查询。
让我们考虑对人口普查数据进行查询,在没有差分隐私。
“数据集中有多少人是40岁或以上?”
老样子,获取数据~
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
adult = pd.read_csv("adult_with_pii.csv")
输入查询代码
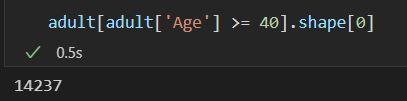
adult[adult['Age'] >= 40].shape[0]
关键的挑战是添加足够的噪声来满足差分隐私的定义,但又不能过多地使答案变得过于嘈杂而无用。
为了使这个过程更容易,在差分隐私领域已经开发了一些基本机制,这些机制准确地描述了使用哪种噪声以及使用多少噪声。
其中之一被称为拉普拉斯机制。(哈哈哈哈喜闻乐见的拉普拉斯机制)
根据拉普拉斯机制,对于返回数字的函数 f ( x ) f(x) f(x),以下 F ( x ) F(x) F(x)定义满足 ϵ \epsilon ϵ-差分隐私:
F ( x ) = f ( x ) + Lap ( s ϵ ) F(x) = f(x) + \textsf{Lap}(\frac{s}{\epsilon}) F(x)=f(x)+Lap(ϵs)
其中 s s s是 f f f的敏感度, Lap ( S ) \textsf{Lap}(S) Lap(S)表示从中心为 0 且比例为 S S S的拉普拉斯分布中采样。
函数 f f f的灵敏度是当其输入变化 1 时, f f f的输出变化量。
灵敏度是一个复杂的话题,也是设计差分隐私算法的一个组成部分。
现在,我们只指出计数查询的敏感性始终为1。
如果查询计算数据集中具有特定属性的行数,然后我们只修改数据集的一行,则查询的输出最多可以更改1。
因此,我们可以通过使用灵敏度为 1 的拉普拉斯机制和我们选择的 ϵ \epsilon ϵ来实现示例查询的差分隐私。
现在,让我们选择 ϵ = 0.1 \epsilon = 0.1 ϵ=0.1。我们可以使用Numpy的从拉普拉斯分布中采样。
sensitivity = 1
epsilon = 0.1
adult[adult['Age'] >= 40].shape[0] + np.random.laplace(loc=0, scale=sensitivity/epsilon)
每次,输出都会发生变化,但大多数时候,答案与真实答案14235足够接近,因此很有用。
多少噪音就足够了?(How Much Noise is Enough?)
那么另一个问题来了~
我们怎么知道拉普拉斯机制增加了足够的噪声来防止数据集中个体的重新识别?
让我们尝试写个攻击吧~
让我们写下一个恶意计数查询,该查询专门用于确定Karrie Trusslove的收入是否大于5万美元。
karries_row = adult[adult['Name'] == 'Karrie Trusslove']
karries_row[karries_row['Target'] == '<=50K'].shape[0]
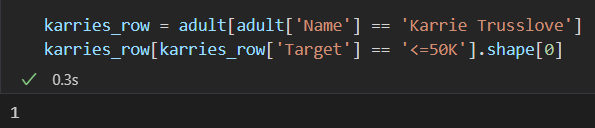
这个结果肯定侵犯了Karrie的隐私,因为它揭示了Karrie行的收入列的价值。
由于我们知道如何使用拉普拉斯机制确保对查询进行计数的差异隐私,因此我们可以对以下查询执行此操作:
sensitivity = 1
epsilon = 0.1
karries_row = adult[adult['Name'] == 'Karrie Trusslove']
karries_row[karries_row['Target'] == '<=50K'].shape[0] + \
np.random.laplace(loc=0, scale=sensitivity/epsilon)
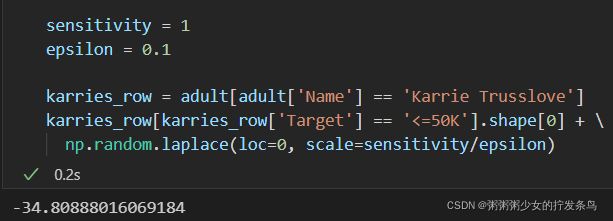
这是我跑的第一次,直接来个负数~
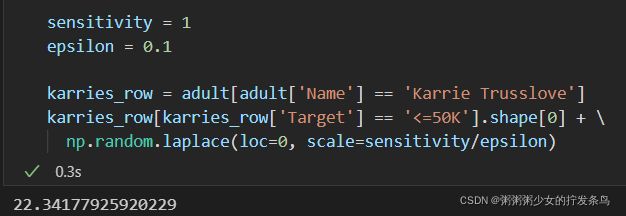
第二次的结果还正常~
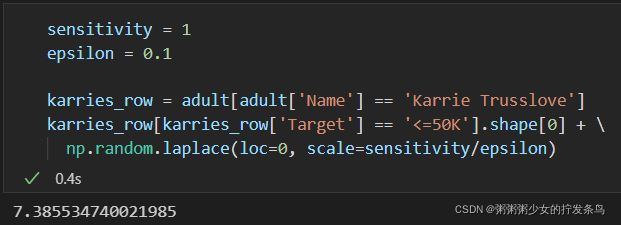
第三次比较接近1,但是看不出来哈哈哈哈哈~
真正的答案是0还是1?噪音太大,无法可靠地分辨出来。
这就是差别隐私的工作方式,该方法不会拒绝被确定为恶意的查询。
相反,它增加了足够的噪音,恶意查询的结果对对手毫无用处。
总结
1、与 k k k-Anonymity不同,差分隐私是算法的属性,而不是数据的属性。也就是说,我们可以证明算法满足差分隐私。
2、随机函数 F F F中的随机性应该是"足够的",以便从 F F F观察到的输出不会揭示 x x x或 x ′ x' x′中哪一个是输入。
3、当 ϵ \epsilon ϵ越小时,数据效用越低,隐私保护程度越高;当 ϵ \epsilon ϵ越大时,数据效用越高,隐私保护程度越低。
4、普遍的共识是 ϵ \epsilon ϵ应该在1左右或更小,并且 ϵ \epsilon ϵ的值高于10可能对保护隐私没有多大作用 ,但这个经验法则可能会变得非常保守。
5、拉普拉斯机制不会拒绝被确定为恶意的查询,相反,它增加了足够的噪音,恶意查询的结果对对手毫无用处。