【cooper】深度学习入门:基于Python的理论与实现(鱼书)_个人读书笔记
深度学习入门:基于Python的理论与实现(鱼书)
个人笔记
作者:Cooper
第三章神经网络
神经网络的基本样子就是
输入层->中间层(隐藏层)->输出层,每条线代表的就是各个神经元之间的权重,而每个神经元内部还有函数处理,将输入的数值进行一个函数变换,这就是激活函数。
3.2激活函数
3.2.1阶跃函数(step)
数学表示:
阶跃函数就是当输入x大于等于0的时候,输出1,其他时候输出0.
h ( x ) = { 1 , x ≥ 0 0 , x < 0 h(x)=\begin{cases} 1,&x\ge 0\\ %大于等于符号是\ge 0,&x < 0 \end{cases} h(x)={1,0,x≥0x<0
代码表示:
#1
def step_function(x):
if x > 0:
return 1
else:
return 0
#初始版本,照搬公式,但是比更不能处理numply数组,
#例如step_function(np.array([1.0,2.0]))
#2
def step_function(x):
y = x > 0
return y.astype(np.int)
#更新版本,numpy数组会输出布尔型数据,再利用astype将其转换成int类型数据
阶梯函数的图形:
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()
Q
plt.show()图像并不显示
A
1把这个matplotlib重新安装一下,之后有时间再弄
2复习一下如何使用pip指令,在lunix中进场使用pip指令来安装程序,并且其他方法很慢
3.2.2sigmoid函数
数学表示:
h ( x ) = 1 1 + e − x h(x)=\frac{1}{1+e^{-x}} h(x)=1+e−x1
代码表示:
def sigmoid(x):
return 1/(1 + np.exp(-x))
sigmoid的图形:
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()
阶跃函数与sigmoid函数之间的比较:
3.2.3ReLU函数
ReLU(Rectified Linear Unit)函数的数学表达式:
h ( x ) = { x , x ≥ 0 0 , x < 0 h(x)=\begin{cases} x, &x \ge 0\\ 0, &x < 0 \end{cases} h(x)={x,0,x≥0x<0
代码表示:
def relu(x):
return np.maximum(0,x) #maxium会从输入(0和x)中选择较大的输出。
note:
为什么激活的求和函数一定要使用非线性的?
如果使用了线性的,那么无论采用几层的网络其结果仍然是一个线性的,等效于一个函数,但是采用了非线性的,那可能性就很多了。
3.3多维数组
也就是矩阵部分在numpy中的实现,也就是多个行向量堆叠在一起实现矩阵,而非matlab中的列向量。
3.3.1多维数组的维度和形状
a = np.array([[1, 2,3],[2, 3,4]])
a.ndim #维度,输出2,整型int类型,就是说shape中有几个数字就是几
a.shape #形状,输出(2,3),元组tuple类型,就是矩阵的行列数
b = np.array([[1,2,3],[2,3,4],[3,4,5]])
b.ndim #维度,输出3,整型int类型,是shape中的几个数字。
a.shape #形状,输出(2,4),元组tuple类型,就是矩阵的行列数,就算只有一行也是元组类型
3.3.2多维数组的点乘
满足一切关于矩阵的法则,区分左右乘,并且需要满足乘法法则
np.dot(a,b)
输出为:
array([[14, 20, 26],
[20, 29, 38]])
3.4 三层神经网络的实现
3.4.1单层步骤
3层神经网络主要指的是1个输入层,2个隐藏层,1个输出层,本书指的是只算中间的连接,这样叫做3层
第一层:
从输入层到隐藏层第一层,主要是输入X*连接的权重和偏置,之后到神经元激活处理。
X = np.array([1.0, 0.5])
#输入神经元主要有两个,输入数值分别是1.0 ,0.5
W1 = np.array([[0.1, 0.3, 0.5],[0.2, 0.4, 0.6]])
#由于输入2,隐藏层1有3个,所以矩阵表示,第一个神经元对于下一级三个隐藏层神经元的权值
#分别为 0.1, 0.3, 0.5 矩阵第二层同理。
B1 = np.array([0.1, 0.2, 0.3])
#分别表示对三个隐藏层神经元的偏置
print(W1.shape) # (2, 3)
print(X.shape) # (2,)
print(B1.shape) # (3,)
A1 = np.dot(X, W1) + B1
#至此,完成了输入层到隐藏层的过程
激活层处理:
Z1 = sigmoid(A1)
#这里采用激活函数sigmoid处理
print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252, 0.66818777, 0.75026011]
#第一层的输出就是这个Z1
最终第一层的输出结果为:[0.57444252, 0.66818777, 0.75026011]
第二层:
类似于第一层的处理流程,逻辑一样。
W2 = np.array([[0.1, 0.4], [0.2,0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
A2 = np.dot(Z1,W2) + B2
print(A2) #[0.51615984 1.21402696]
print(A2.shape) #(2,)
print(W2.shape) #(3, 2)
print(B2.shape) #(2,)
激活层处理
Z2 = sigmoid(A2)
print(Z2) #[0.62624937 0.7710107 ]
print(Z2.shape) #print(Z2.shape)
所以第二层最终的输出为[0.62624937 0.7710107 ]
第三层:
就是从隐藏层到输出层的流程,定义了一个从隐藏层到输出层的函数identity,就是保持函数
def identity_function(x):
return x
W3 = np.array([[0.1, 0.3],[0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2,W3) + B3
Y=identity_function(A3)
print(Y)#[0.31682708 0.69627909]
3.4.2整合设计
首先构造一个初始化函数,包括每一层的权值和偏置,其中权重为大写字母,偏置和中间结果是小写字母。
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
前向传递函数,就是其中的激活步骤和传递三次全部整合,如下:
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
接着输入参数,观察网络情况:
network = init_network() #初始化
x = np.array([1.0, 0.5]) #传入输入参数
y = forward(network, x) #前向函数
print(y) # [ 0.31682708 0.69627909] #输出结果
得到结果为[ 0.31682708 0.69627909]
3.5输出层的设计
神经网络主要有两个用途:分类和回归(预测),一般需要根据不同的问题设置不同的输出层激活函数。
其中回归问题(数值预测)主要采用恒等函数,分类问题主要采用softmax函数。
3.5.1归一化函数(softmax函数)
数据归一化处理:把原本的值映射到0到1之间。
softmax函数干的事就是把全部的数转换成指数,然后计算他在这些指数和中的比例。
数学表达式:
y k = e a k ∑ i = 1 n e i \begin{equation*} y_{k}=\frac{e^{a_{k}}}{\sum_{i=1}^{n}e^{i}} \end{equation*} yk=∑i=1neieak
代码表示:
#1这种方式不能满足溢出问题,当输入x过大时会出现nan的情况
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
#2
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢出对策 同时减去一个最大值,指数函数不变
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
解释例子:
x = np.array([0.3, 2.9, 4.0])
y = softmax(x)
print(y) #[0.01821127 0.24519181 0.73659691]
指数运算是数量级的增长,很小号计算机内存,如果数据太大就会出现无法计算的情况:
x = np.array([1010,1000,990])
y = softmax(x)
print(y)
输出结果为[nan nan nan]
softmax其数字特征:输出求和的值为1,符合概率分布问题
第四章 神经网络的学习
4.2损失函数(loss function)
作为评价权重的好坏指标,有这个指标进行修改权重,主要使用的函数为均方误差和交叉熵误差。
4.2.1均方误差MSE( mean squared error)
数学表达式:
E = 1 2 ∑ i = 1 n ( y k − t k ) 2 E = \frac{1}{2} \sum^{n}_{i=1} (y_{k}-t_{k})^{2} E=21i=1∑n(yk−tk)2
其中yk是神经网络的输出结果,tk是监督数据也就是01,k表示第几个数据。
监督数据的表示方法:
one-hot表示方法:
比如某一组数据监督数据正确的解为2,采用one-hot方式的话,标签的表示方式就是标签“2”为1,其他标签“0”,“5”都取0,这就是one-hot表示方法。
t = [0, 0, 1, 0, 0, 0, 0,]
非one-hot表示方法(标签)形式:
直接把正确答案表示出来,比如“2”,“7"。
t = [2, 5, 7, 2]
总结就是这样的:假设标注结果是2
one-hot: t = [0, 0, 1, 0, 0, 0, 0,]
标签: t = [2]
代码表示:
def mean_squard_error(y,t):
return 0.5*np.sum((y-t)**2)
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0,]
#例“2”的概率最高的情况(0.6)
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(mean_squard_error(np.array(y), np.array(t)))
输出为0.097500000000000031,由此可知输出的结果和很小,也就是误差很小。
4.2.2交叉熵误差CEE(cross entropy error)
单个数据的交叉熵误差数学表示:
E = − ∑ i = 1 n t k log y k E= -\sum^{n}_{i=1} t_{k} \log y_{k} E=−i=1∑ntklogyk
其中tk同样是监督数据,yk也是网络输出,这些都是一组数据。
实际上,当监督数据采用one-hot表示的时候,计算的只有正确的输出的自然对数。比如,当正确的解为2,只是计算了0.6的自然对数.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t*np.log(y+delta))
#加入一个小量,防止出现log0的情况
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(cross_entropy_error(np.array(y), np.array(t)))
#实际上此时计算的只有-np.log(0.6)
4.2.3mini-batch上的交叉熵
mini-batch的思路就是类似电视收视率,以样本代替整体,随机选取一部分样本求交叉熵。
数学表达式:
E = − 1 N ∑ j = 1 N ∑ i = 1 n t k log y k E= -\frac{1}{N} \sum^{N}_{j=1} \sum^{n}_{i=1} t_{k} \log y_{k} E=−N1j=1∑Ni=1∑ntklogyk
这里假设这一批有N个数据,每一局数据求一次交叉熵,之后再求和,在平均。
类似之前的方法,我们也只需要知道每批次正确的数据值,然后将该批次正确的值求和,就可以得到总的cee。
代码表示:
#输入数据y是二维数组
def cross_entropy_error(y, t):
if y.ndim == 1: #如果只是一个数据的交叉熵
t = t.reshape(1, t.size)#t.size就是有多少个矩阵里面有多少个元素
y = y.reshape(1, y.size)#比如2*2的矩阵size就为4
#上述操作就是把y展开成1维的
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
首先解释一下这个np.arange(batch_size)代码部分,这一部分说的是,按照等差数列,公差为1,从0开始,到batch_sizebatch_size-1结束。例如np.arange(5)它的输出形式为:array([0, 1, 2, 3, 4]),此时,标签数据集t的表示方式为[2, 7, 0, 9, 4] (第一个正确标签为2,第二个正确标签为7),然后,这两个一维数组通过numply的广播机制组成输出数组的二维下标,用来表示正确的结果的概率大小。,是这个样子滴[y[0,2], y[1,7], y[2,0], y[3,9], y[4,4]],y[0,2]表示二维数组y下标为0,2时得数据大小。
4.3数值微分
4.3.1导数
就是数值分析里面的方法,取h为一个很小的量,代替真正的导数:
导数的定义:
d f ( x ) d x = lim h → 0 f ( x + h ) − f ( x ) h \frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} dxdf(x)=h→0limhf(x+h)−f(x)
数值微分中的定义:
d f ( x ) d x ≈ f ( x + h ) − f ( x ) h \frac{df(x)}{dx} ≈\frac{f(x+h)-f(x)}{h} dxdf(x)≈hf(x+h)−f(x)
代码形式:
def numerical_diff(f, x):
h = 10e-50
return (f(x+h) - f(x)) / h
4.3.2偏导数
对于多元函数的导数的求法,就是偏导数问题的引出,例如下面:
f ( x 0 , x 1 ) = x 0 2 + x 1 2 f(x_{0},x_{1}) = x_{0}^{2} + x_{1}^{2} f(x0,x1)=x02+x12
利用代码实现就是如下形式:
def function_2(x):
return x[0]**2 + x[1]**2
4.4梯度
利用中间差值的方法,求每一个值的偏导数,然后按照坐标形式排列,就得到梯度。
def numberical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val
return grad
numberical_gradient(function_2,np.array([3.0,4.0]))
输出为array([6., 8.])
numberical_gradient(function_2,np.array([0.0,2.0]))
输出为array([0., 4.])
numberical_gradient(function_2,np.array([3.0,0.0]))
输出为array([6., 0.])
梯度也就是各个方向函数值减少最多的方向,在二维平面中,就是x和y方向减少最多的方向。
4.4.1梯度法
梯度法就是寻找最优参数的。
利用数学公式表示如下:
x 0 = x 0 − η ∂ f ∂ x 0 x 1 = x 1 − η ∂ f ∂ x 1 x_{0} = x_{0} - \eta \frac{\partial f}{\partial x_{0}}\\ x_{1} = x_{1} - \eta \frac{\partial f}{\partial x_{1}} x0=x0−η∂x0∂fx1=x1−η∂x1∂f
其中,η表示更新量,也称为学习率(learning tate),梯度法就是以一定的学习率和步长逼近最小值。
def gradient_descent(f ,init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_descent(f,x)
x -= lr*grad
return x
这也算是最优化理论的一种方法,其中f表示需要初始化的函数,init_x表示初始值,lr表示learning rate, sterp_num表示梯度法的重复次数。numerical_descent(f,x)用来求解函数的梯度。
def function_2(x):
return x[0]**2+x[1]**2
init_x=np.array([-3.0,4.0])
gradient_descent(function_2,init_x=init_x,lr=0.1,step_num=100)
得到输出结果为:array([ -6.11110793e-10, 8.14814391e-10])其实结果就为(0,0)。
在调节参数的过程中,学习率是一个超参数,这个参数过大或者过小均不能娶到很好的结果,这个数值需要根据经验试出来。
#学习率过大
init_x=np.array([-3.0,4.0])
gradient_descent(function_2,init_x=init_x,lr=10.0,step_num=100)
123
输出为array([-2.58983747e+13, -1.29524862e+12])
#学习率过小
init_x=np.array([-3.0,4.0])
gradient_descent(function_2,init_x=init_x,lr=1e-10,step_num=100)
123
输出为array([-2.99999994, 3.99999992])
4.4.2神经网络的梯度
神经网络的学习要求解梯度?(为什么要求解这个矩阵,有什么好处)。
$$
\begin{aligned}%整体行文左对齐
W = & %换行符号,维持列的方式
\begin{pmatrix}
w_{11} & w_{12} &w_{13}\
w_{21} & w_{22} &w_{23}
\end{pmatrix}
\
\frac{\partial L}{\partial W} =& %这个&可是维持左对齐的精髓,是用行列式的方式使其对齐
\begin{pmatrix}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}}
\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}}
\end{pmatrix}
\end{aligned} %整体行文左对齐
$$
对于第二个矩阵,我们也称之为海森矩阵(Hessian Matrix)。
4.5学习算法的实现
学习过程主要分为以下几步:
step1(mini-batch)
由于样本数据集很大,所以我们随即从其中选取一部分数据作为训练数据。主要目的是为了减少min-batch的损失函数的值
step2(计算梯度)
为了减少mini-batch的损失函数的值,我们需要求出每个权重减少最快的方向,也就是这个权重的梯度。
step3(更新参数)
将权重沿着梯度的方向更新。
step4(重复)
重复上面的123
4.5.1双层神经网络
class TwoLayerNet:
def init(self,input_size,hidden_size,output_size,weight_init_std=0.01):
#初始化权重
self.params={}
self.params[‘W1’]=weight_init_stdnp.random.randn(input_size,hidden_size)
self.params[‘b1’]=np.zeros(hidden_size)
self.params[‘W2’]=weight_init_stdnp.random.randn(hidden_size,output_size)
self.params[‘b2’]=np.zeros(output_size)
def predict(self,x):
W1,W2=self.params['W1'],self.params['W2']
b1,b2=self.params['b1'],self.params['b2']
a1=np.dot(x,W1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,W2)+b2
y=softmax(a2)
return y
#x为输入数据,t为监督数据
def loss(self,x,t):
y=self.predict(x)
return cross_entropy_error(y,t)
def accuracy(self,x,t):
y=self.predict(x)
y=np.argmax(y,axis=1)
t=np.argmax(t,axis=1)
accuracy=np.sum(y==t)/float(x.shape[0])
return accuracy
#x为输入数据,t为监督数据
def numberical_gradient(self,x,t):
loss_W=lambda W: self.loss(x,t)
grads={}
grads['W1']=numberical_gradient(loss_W,self.params['W1'])
grads['b1']=numberical_gradient(loss_W,self.params['b1'])
grads['W2']=numberical_gradient(loss_W,self.params['W2'])
grads['b2']=numberical_gradient(loss_W,self.params['b2'])
return grads
4.5.2对于测试数据的评价
神经网络的学习中必须确认网络能否识别训练数据之外的其他数据,就是确认是否会发生过拟合。过拟合就是说网络只认识训练集里面的图片,不在训练集的图片无法识别。
神经网络最终目的是掌握学习的泛化能力,就是训练集之外的数据也能认识,为了记录训练情况,我们没经过一个epoch就会记录训练数据和测试数据的识别精度。(epoch是一个单位,Epoch的值就是整个训练数据集被反复使用几次)
第五章 误差反向传播算法(BP)
采用计算图的方法来讲解反向传播的过程,但是我更倾向于使用公式推导,也就是链式法则,每一次链式法则均代表反向传播一次。
5.4简单层的实现
这里只是简单地介绍了两种节点,乘法层(MulLayer),加法节点的加法层(AddLayer)。
5.4.1乘法层的实现
class MulLayer:
def __init__(self):
self.x=None
self.y=None
def forward(self,x,y):
self.x=x
self.y=y
out=x*y
return out
def backward(self,dout):
dx=dout*self.y
dy=dout*self.x
return dx,dy
forard()接收两个参数,将他们相乘之后输出,backward()将上游传来的导数(dout)乘以正向传递的两个翻转值,之后传递给下游。
正向传播:
apple=100
apple_num=2
tax=1.1
#layer
mul_apple_layer=MulLayer()
mul_tax_layer=MulLayer()
#forward
apple_price=mul_apple_layer.forward(apple,apple_num)
price=mul_tax_layer.forward(apple_price,tax)
print(price)
最终得到价格220
各个变量的导数可以由backward()求出来。
#backward
dprice=1
dapple_price, dtax=mul_tax_layer.backward(dprice)
dapple,dapple_num=mul_apple_layer.backward(dapple_price)
print(dapple,dapple_num,dtax)
最终输出结果为: 2.2 110 200
5.4.2加法层的实现
就是计算图中的加法关系。
class AddLayer:
def __init__(self):
pass
def forward(self,x,y):
out=x+y
return out
def backward(self,dout):
dx=dout*1
dy=dout*1
return dx,dy
5.5激活层函数
5.5.1ReLU层
ReLU(Rectified Linear Unit)可以由下式表示。
y = { x , x ≥ 0 0 , x < 0 y = \begin{cases} x, &x ≥ 0\\ 0, &x < 0 \end{cases} y={x,0,x≥0x<0
然后,对上式求y关于x的导数,可以得到如下结果。
∂ y ∂ x = { 1 , x ≥ 0 0 , x < 0 \frac{\partial{y}}{\partial{x}}= \begin{cases} 1, &x ≥ 0\\ 0, &x < 0 \end{cases} ∂x∂y={1,0,x≥0x<0
从实际使用效果来看,如果正向传播的输入大于0时,反向传播就会原封不动传递给下游;如果正向传播的数值小玉0,反向传播的信号就会在这里停止。
代码表示:
class Relu:
def __inin__(self):
self.mask=None
def forward(self,x):
self.mask=(x<=0)
out=x.copy()
out[self.mask]=0
return out
def backward(self,dout):
dout[self.mask]=0
dx=dout
return dx
其中有一个类,mask,这个变量是一个bool型变量,将正向输入小于等于0的地方变为True,然后反向传播的时候将他们变成0。
5.5.2sigmoid层
就是之前的激活函数表示方法:
y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
求得反向传播导数为:
∂ L ∂ y = y ( 1 − y ) \frac{\partial L}{\partial y} =y(1-y) ∂y∂L=y(1−y)
代码表示如下:
class Sigmoid:
def __init__(self):
self.out=None
def forward(self,x):
out=1/(1+np.exp(-x))
self.out=out
return out
def backward(self,dout):
dx=dout*(1.0-self.out)*self.out
return dx
5.6Affine/Softmax层的实现
5.6.1 Affine层
也就是y = x*w+b这一步按照前行和反向传播的方法重新书写一遍。
数学推导部分,暂时不会
直接上代码部分:
class Affine:
def __init__ (self,W,b):
self.W=W
self.b=b
self.x=None
self.dW=None
self.db=None
def forward(self,x):
self.x=x
out=np.dot(x,self.W)+self.b
return out
def backward(self,dout):
dx=np.dot(dout,self.W.T)
self.dW=np.dot(self.x.T,dout)
self.db=np.sum(dout,axis=0)
return dx
5.6.3 Softmax-with-Loss层
反向传播最终能得到y-t这样的结果,也就是将误差向前传递,用来修改权重的参数。
class SoftmaxWithLoss:
def __init__(self):
self.loss=None
self.y=None
self.t=None
def forward(self,x,t):
self.t=t
self.y=softmax(x)
self.loss=cross_entropy_error(self.y,self.t)
return self.loss
def backward(self,dout=1):
batch_size=self.t.shape[0]
dx=(self.y-self.t)/batch_size
return dx
第六章 与学习相关的技巧
6.1参数的更新
寻找损失函数尽可能小的参数。就是最优化,但很难,我们采用SGD。
6.1.1 SGD
他的数学核心就是这一行公式:
W ← W − η ∂ L ∂ W W \gets W-\eta\frac{\partial L}{\partial W} W←W−η∂W∂L
代码形式如下所示:
class SGD:
def __init__(self,lr=0.01):
self.lr=lr
def update(self,params,grads):
for key in params.keys():
params[key]-=self.lr*grads[key]
SGD他的优缺点:
他并不能很好地适应寻找最小点的情况,它所寻找的梯度是每一部分的极小点,极小点不一定和最小点重合。
6.1.2 Momentum
Momentum代表动量,也就是运动能量大小的意思,采用数学表示如下:
W ← α v − η ∂ L ∂ W W ← W + v W \gets \alpha v-\eta\frac{\partial L}{\partial W} \\ W \gets W + v W←αv−η∂W∂LW←W+v
就是整体的下降不再是随机方向的,而是给定一个初速度,演这个方向进行梯度下降搜索。
代码表示如下:
class Momentum:
def init(self,lr=0.01,momentum=0.9):
self.lr=lr
self.momentum=momentum
self.v=None
def update(self,params,grads):
if self.v is None:
self.v={}
for key, val in params.items():
self.v[key]=np.zeros_like(val)
for key in params.keys():
self.v[key]=self.momentum*self.v[key]-self.lr*grads[key]
params[key]+=self.v[key]
6.1.3 AdaGrad
有关技巧中,有一种被称为学习率衰减(learning rate decay)的方法,这里我们选择AdaGrad。
数学公式如下:
h ← h + ∂ L ∂ W ∂ L ∂ W W ← W − η 1 h ∂ L ∂ W h \gets h + \frac{\partial L}{\partial W}\frac{\partial L}{\partial W} \\ W \gets W -\eta\frac{1}{\sqrt{h}} \frac{\partial L}{\partial W} h←h+∂W∂L∂W∂LW←W−ηh1∂W∂L
class AdaGrad:
def __init__(self,lr=0.01):
self.lr=lr
self.h=None
def update(self,params,grads):
if self.h is None:
self.h={}
for key, val in params.items():
self.h[key]=np.zeros_like(val)
for key in params.keys():
self.h[key]+=grads[key]*grads[key]
params[key]-=self.lr*grads[key]/(np.sqrt(self.h[key])+1e-7)
6.1.4 Adam
Adam就是将上面两种方法合并,融合了AdaGrad和Momentum两种方法。
那究竟使用哪种优化方法呢,这个得一个个试,没有统一的答案。
6.2 权重的初始值
6.2.1 可以将权重初始值设置为0吗?
达咩,不行,如果将初始值设置为0,然后向后传播,所有元素都将为0,之后反向传播的时候,根据传递法则,需要传入正向传递元素,也是0,那么就全部的值都为0了(反向传递乘法部分,交叉相乘)。所以必须采用随机化生成初始值。
6.2.2 隐藏层的激活值分布
隐藏层的激活值(也就是激活函数的输出z1,在单个神经元内部的转换的输出)。
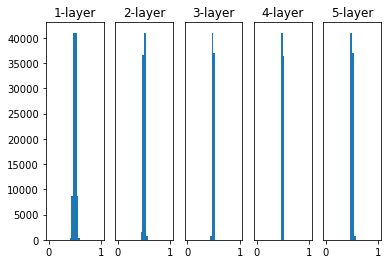
将权值设置为标准差为1的正态分布。
代码如下:
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def ReLU(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 1000个数据 输入100个神经元
node_num = 100 # 各隐藏层的节点(神经元)数
hidden_layer_size = 5 # 隐藏层有5层
activations = {} # 激活值的结果保存在这里
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
#一开始i = 0,所以这一部步跳过,将每次z传递的至向后传递一次,一开始那么写复杂,这直接使用for循环
# 改变初始值进行实验!
w = np.random.randn(node_num, node_num) * 1
# w = np.random.randn(node_num, node_num) * 0.01
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
# 将激活函数的种类也改变,来进行实验!
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z #此时储存的是激活值
# 绘制直方图
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
if i != 0: plt.yticks([], [])
# plt.xlim(0.1, 1)
# plt.ylim(0, 7000)
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
可以看到每一层的激活值均偏向0和1的分布,这是因为sigmoid函数是S函数,随着输入向量变改变,导数值逐渐接近0,所以偏向0和1的数据在传递的过程中不断减少,最终消失,这就是梯度消失问题。
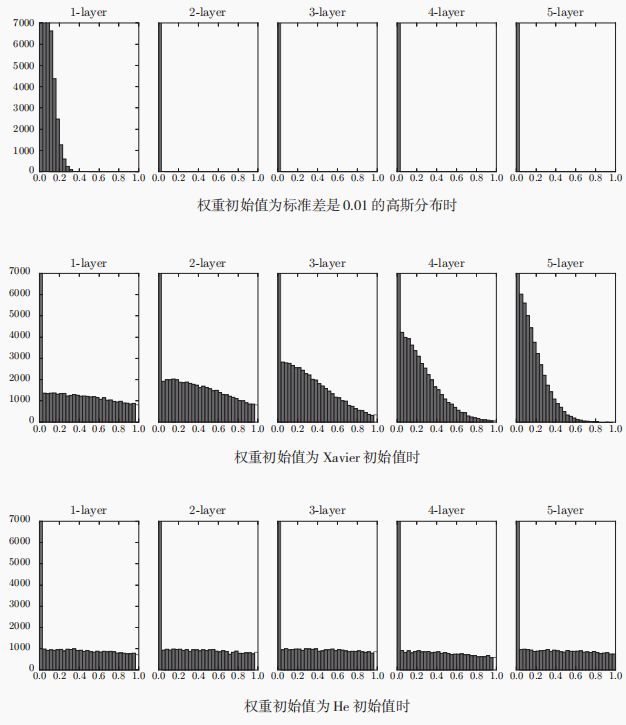
之后将标准差改为0.01的高斯分布后,结果如下图所示。
这回可以看到,数据的分布基本都位于0.5左右,但是有所偏向,这就是表现力,当所有数据均呈现相同的偏向问题,那么表现效果就相当于一个神经元,就会出现"表现力受限"的问题。所以要求激活值都应该具有适应的广度。
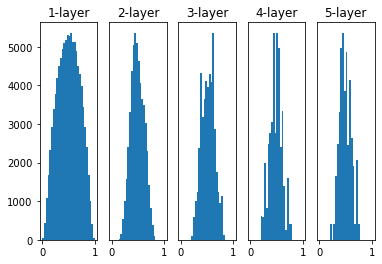
之后,我们采用Xavier等人的初始值,该文章表明,如果前一层的节点为n,那么后面的节点就应该采用标准差为 1 n \frac{1}{\sqrt{n}} n1的分布。
实验结果如下图:
可以看到,每一层的数据都有比之前更广的分布,这就解决了之前数据分布不广的问题,使得sigmoid可以高效的学习。
6.2.3 ReLU的初始权值
Xavier初始值是以激活函数为线性时所提出的,其中sigmoid和tanh均左右对称,所以在中点附近可以视为线性函数,可以使用Xavier作为初始值。
当激活函数为ReLU时,一般使用"He初始值",是标准差为 2 n \sqrt{\frac{2}{n}} n2
的高斯分布。下面,给出了当激活函数为ReLU时,使用三种初始值的激活值分布情况。
总结:
当激活函数选取ReLU的时候,选取He做初始值;
当激活函数选取sigmoid和tanh,选取Xavier初始值。
6.3 Batch Normalization
使得初始值的选取不那么重要,强制调整激活函数值的分布。
简单地将就是将数据变成均值为0,方差为1的高斯函数。
6.4 过拟合与抑制方法
避免过拟合的方法。
6.4.1 过拟合
过拟合问题就是对于训练数据集过分你和,也就是准确度很高,但是测试数据集准确度很低,过拟合主要有两个方面:
- 模型参数过多
- 训练数据过少
6.4.2 权值衰减
权值衰减是一种避免过拟合的方法,该方法对学习中权值变化过大进行惩罚。主要在损失中加入权重的L2范数。
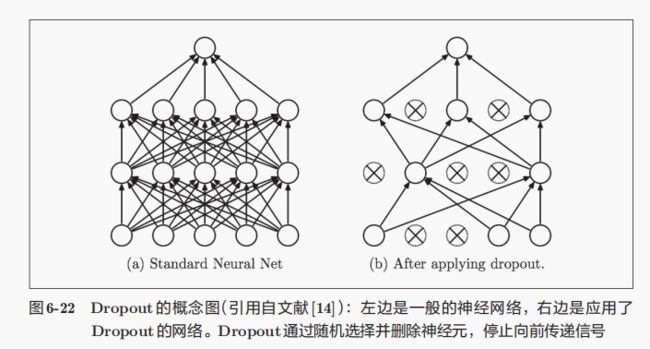
6.4.3 Dropout
神经网络过于复杂的时候该方法便不再使用,于是便使用Dropout的方法,该方法就是在训练中使神经网络的传递过程随机删除部分神经元。
代码如下:
def forward(self,x,train_flg=True):
if train_flg:
self.mask=np.random.rand(*x.shape)>self.dropout_ratio
return x*self.mask
else:
return x*(1.0-self.dropout_ratio)
def backward(self,dout):
return dout*self.mask
该函数在正反向传播中的行为和ReLU相同。
6.5超参数的验证
超参数(hyper-parameter)就是指的需要提前人为设置的数据,比如
神经元数量,batch大小,epoch大小,学习率这些都是超参数,均需要设置正确的值。
6.5.1验证数据
我们一般将数据分成三部分(train,test,validation),其中train是用来学习数据的特征,test是用来检验学习效果,也就是泛华效果,validation就是用来检验超参数的效果如何。
6.5.2超参数的最优化
贫经验循环出来的,可以使用贝叶斯最优化。
第七章 卷积神经网络
本部分将介绍重头戏卷积神经网络(Convolutional Neural Network,CNN)。
7.1卷积层
卷积层的输入输出数据叫做特征图。
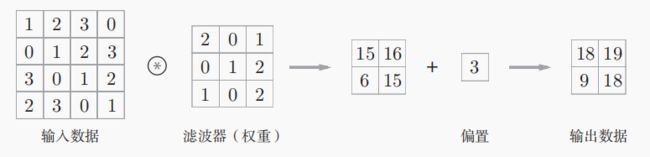
7.1.1卷积运算
卷积核以一定的间隔滑动到输入数据的窗口,并进行对应的乘积累加运算(而非矩阵相乘运算)然后将将对应数据输出。对于偏置直接加到输出结果所有元素上。
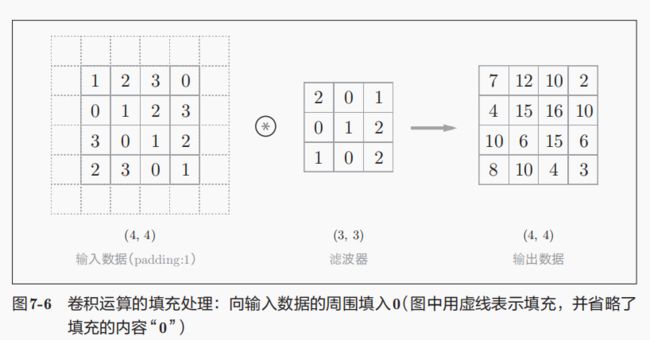
7.1.2填充
卷积运算之后的矩阵会变小,所以向使得输出矩阵大小不变,需要在输入矩阵处理。这就是填充(padding),在矩阵周围填入固定的数据(比如0或者1)。
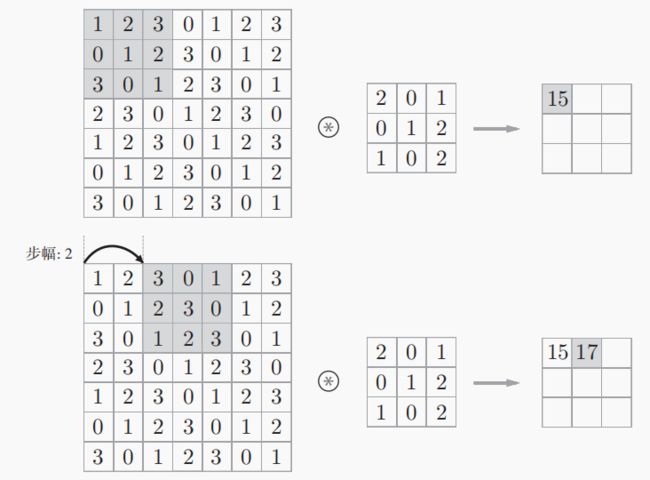
7.1.3步幅
滤波器在输入数据移动的距离叫做步幅(stride)。
输出数据的大小可以采用如下计算公式:
假设输入大小为(H,W)滤波器大小为(FH,FW),输出大小为(OH,OW),填充为P,步幅为S。
O H = H + 2 P − F H S + 1 O W = W + 2 P − F W S + 1 OH = \frac{H+2P-FH}{S} +1 \\ OW = \frac{W+2P-FW}{S} +1 OH=SH+2P−FH+1OW=SW+2P−FW+1
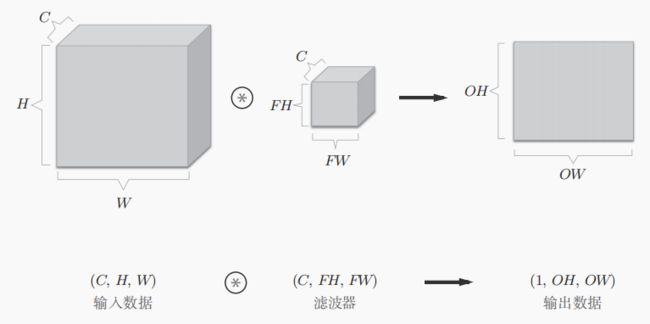
7.1.4三维数据的卷积运算
三维通常指的是,长宽和通道这三个维度。运算过程就是每层单独计算,然后将三层结果相加得到输出。
需要注意,输入数据和滤波器的通道数要设置为相同的值。但是滤波器的大小并不是固定的。
参考动图:
https://cs231n.github.io/assets/conv-demo/index.html
7.1.5多维数组(结合方块)
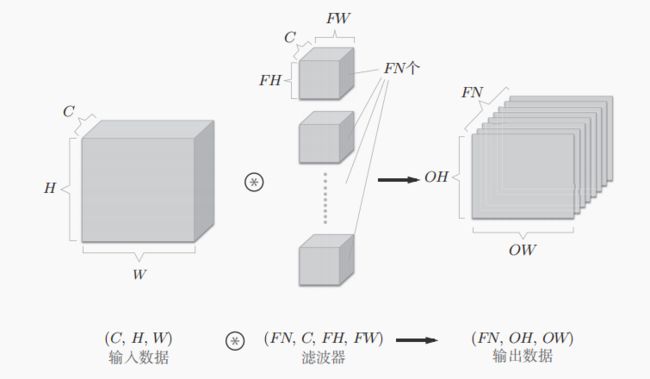
当考虑多位数组的时候,书写顺序如下(channel,height,width),简写为(C,H,W),滤波器也按照这个顺序书写(C,FH,FW)。
如果希望得到FN个输出,那就需要FN个滤波器(权重)。
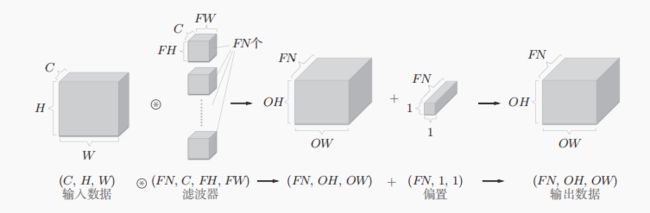
其中滤波器的权重需要按照(ouyput_channel,input_channel,heidght,width)的顺序书写。
当需要添加偏置的时候,可以通过NumPy的广播功能实现。
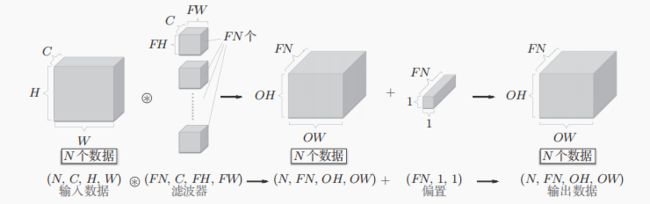
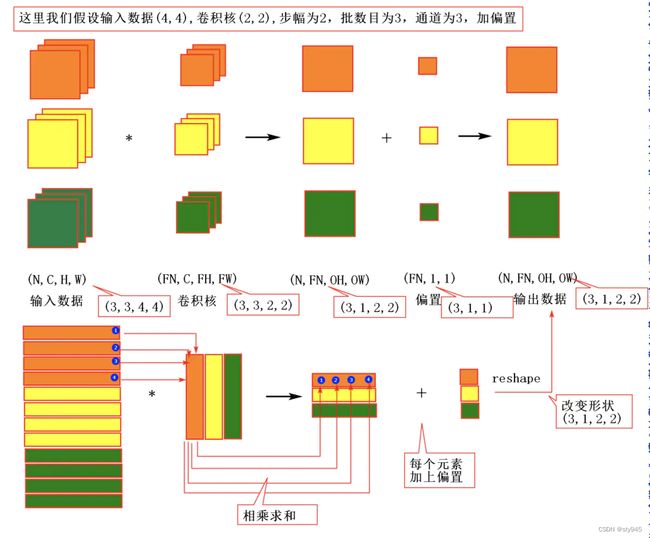
7.1.6批处理
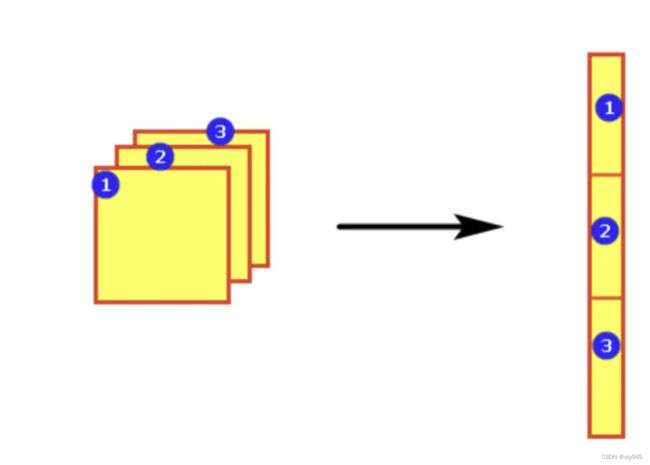
将神经网络的输出数据打包处理,对应之前的批处理(mini-batch),需要注意的是对N个数据进行卷积运算,就是汇总数据变成1次。
其中进行了批量的im2col处理,将4维的输入数据(通道数,通道,高,长)转换成2维矩阵。
然后需要对滤波器进行相应的变换,之后才能对他做矩阵乘法
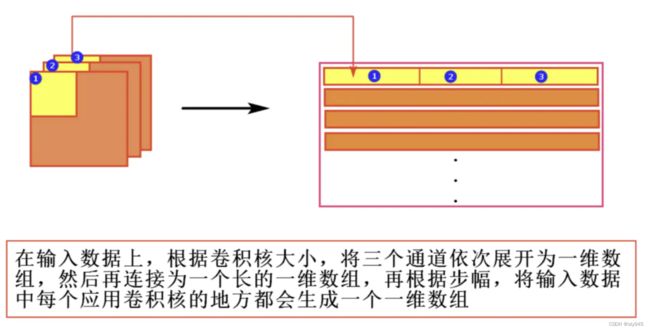
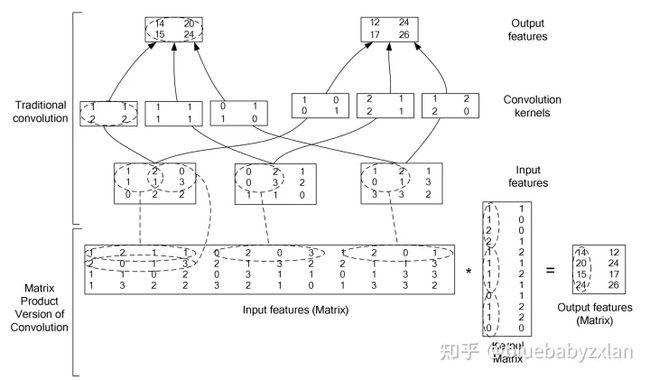
7.1.7im2col函数的处理过程
对于输入数据矩阵的二维处理过程:
对于卷积核的二维处理过程:
关于两者之后进卷积处理行的过程如下:
可以看到采用im2col的方法实现的计算效率很高。
参考文献:
https://blog.csdn.net/sty945/article/details/125135444
https://blog.csdn.net/dwyane12138/article/details/78449898
https://zhuanlan.zhihu.com/p/546871247
7.1.8卷积层的代码实现
class Convolution:
def __init__(self,W,b,stride=1,pad=0):
self.W=W
self.b=b
self.stride=stride
self.pad=pad
def forward(self,x):
FN,C,FH,FM=self.W.shaoe
N,C,H,W=x.shape
out_h=int(1+(H+2*sel.pad-FH)/self.stride)
out_w=int(1+(W+2*sel.pad-FW)/self.stride)
col=im2col(x,FH,FW,self.stride,self.pad)
col_w=self.W.reshape(FN,-1).T
#这里其实可以直接处理成下面的式子,不需要转置
#col_w=self.W.reshape(-1,FN)
out=np.dot(col,col.W)+self.b
out=out.reshape(N,out_h,out_w,-1).transpose(0,3,1,2)
return out
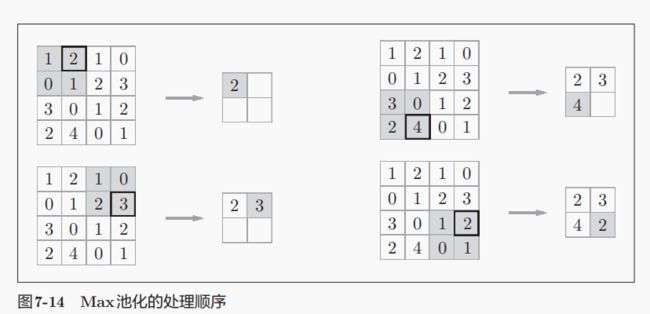
7.2池化层
池化是缩小空间的运算,可以把大的空间变成小的。
池化层的特征:
- 没有要学习的参数
- 通道数不发生改变
- 对于微小的改变不发生变动,也就是鲁棒性健壮。
代码实现: