机器学习实战读书笔记:第二章 线性回归及延伸
机器学习实战读书笔记
第二章 线性回归及延伸
疫情留在宿舍无聊,看书时突然发现自己以前学的知识点在需要回顾时,都得把书再扫一遍,或者去各个文件夹里面找资料。所以,将它存放在此,其中应该会有很多错误,希望大佬们路过的时候帮忙纠正一下,谢谢!
文章目录
- 机器学习实战读书笔记
- 前言
- 一、各回归模型的区别与联系
-
- 1.1 多项回归与其它的区别
- 1.2 其它回归模型的区别与联系
- 1.2.1 区别
- 1.2.2 联系
- 1.2.3 应用场景
- 二、sklearn代码
-
- 2.1 线性回归
- 2.1.1 数据准备
- 2.1.2 LinearRegresssion
- 2.1.3 Ridge
- 2.1.4 Lasso
- 2.1.5 ElasticNet
- 2.2 多项回归
前言
书中是将梯度下降及部分延伸与线性回归(及其延伸:多项回归、岭回归、Lasso回归、弹性网络)放在一起。此处,只描述线性回归(及其延伸),不讨论逻辑回归、梯度下降(留于深度学习讨论)等。
此处,默认明白损失函数、正则化、最小二乘法等基础理论。
一、各回归模型的区别与联系
1.1 多项回归与其它的区别
与其说多项回归是一种模型,不如说多项回归是一种基于线性回归的处理方式。它将原有特征进行扩展,再对扩展特征上训练一个线性模型。
1.2 其它回归模型的区别与联系
1.2.1 区别
- 线性回归(LinearRegresssion):损失函数MSE;
- 岭回归(Ridge):损失函数MSE+L2正则;
- Lasso回归(Lasso):损失函数MSE+L1正则;
- 弹性网络(ElasticNet):损失函数MSE+L1正则+L2正则。
1.2.2 联系
- 损失函数都是在MSE基础上正则化;
- 都是最小二乘法。
1.2.3 应用场景
- 在绝大多数情况下,不选择纯线性回归,需要加正则化;
- 默认情况下,选择L2正则化(欧式距离),即Ridge回归;
- 在很多特征不需要时,选择Lasso回归或者弹性网络;
- 一般情况下,弹性网络优于Lasso回归,因为Lasso不稳定。
二、sklearn代码
2.1 线性回归
在这些算法的类函数后加了CV,即RidgeCV,其算法与Ridge相同,只是封装了交叉验证,故此处不再调用。
2.1.1 数据准备
import numpy as np
import matplotlib.pyplot as plt
X=3*np.random.rand(100,1)
y=3+5*X+np.random.randn(100,1)
X_new=np.array([[0],[2]])
#绘图
plt.plot(X,y,'b.')
plt.show()
2.1.2 LinearRegresssion
from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
lin_reg.fit(X,y)
print(lin_reg.intercept_,lin_reg.coef_) #偏置项及权重项
#[2.79505567] [[5.1727278]]
y_predict=lin_reg.predict(X_new) #预测
print(y_predict)
'''
[[ 2.79505567]
[13.14051128]]
'''
#绘图
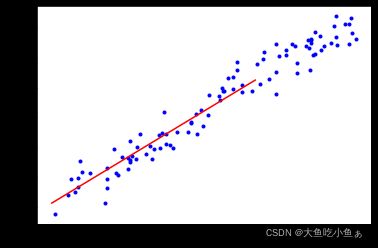
plt.plot(X,y,'b.')
plt.plot(X_new,y_predict,'r-')
plt.show()
2.1.3 Ridge
from sklearn.linear_model import Ridge
lin_reg=Ridge(alpha=1,solver='cholesky')
lin_reg.fit(X,y)
print(lin_reg.intercept_,lin_reg.coef_) #偏置项及权重项
#[2.91085187] [[5.10135051]]
y_predict=lin_reg.predict(X_new) #预测项
print(y_predict)
'''
[[ 2.91085187]
[13.1135529 ]]
'''
#绘图
plt.plot(X,y,'b.')
plt.plot(X_new,y_predict,'r-')
plt.show()
2.1.4 Lasso
from sklearn.linear_model import Lasso
lin_reg=ElasticNet(alpha=0.1)
lin_reg.fit(X,y)
print(lin_reg.intercept_,lin_reg.coef_) #偏置项及权重项
#[3.4498261] [4.76912442]
y_predict=lin_reg.predict(X_new) #预测项
print(y_predict)
#[ 3.4498261 12.98807495]
#绘图
plt.plot(X,y,'b.')
plt.plot(X_new,y_predict,'r-')
plt.show()
2.1.5 ElasticNet
from sklearn.linear_model import ElasticNet
lin_reg=ElasticNet(alpha=0.1,l1_ratio=0.5)
lin_reg.fit(X,y)
print(lin_reg.intercept_,lin_reg.coef_) #偏置项及权重项
#[3.4498261] [4.76912442]
y_predict=lin_reg.predict(X_new) #预测项
print(y_predict)
#[ 3.4498261 12.98807495]
#绘图
plt.plot(X,y,'b.')
plt.plot(X_new,y_predict,'r-')
plt.show()
可视化如下:
由于Lasso即弹性网络不稳定,其拟合偏差与实际相差较大。
2.2 多项回归
import numpy as np
from sklearn.preprocessing import PolynomialFeatures#多项扩展特征
from sklearn.linear_model import LinearRegression
#准备数据
X=6*np.random.rand(100,1)-3
y=2*X**2+3*X+3+np.random.randn(100,1)
poly_features=PolynomialFeatures(degree=2,include_bias=False)#扩展特征
X_poly=poly_features.fit_transform(X) #说明PolynomialFeatures是个转换器
print(X[0])
#[2.78174875]
print(X_poly[0])
#[2.78174875 7.7381261 ]
lin_reg=LinearRegression()
lin_reg.fit(X_poly,y)
print(lin_reg.intercept_,lin_reg.coef_) #偏置项及权重项
#[2.97244697] [[2.97364364 1.99540002]]