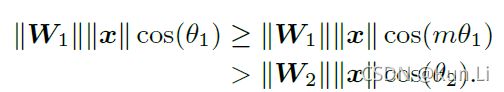large-margin softmax loss for convolutional neural networks

损失函数改进之Large-Margin Softmax Loss_AI之路-CSDN博客_large margin softmax最近几年网络效果的提升除了改变网络结构外，还有一群人在研究损失层的改进，这篇博文要介绍的就是较为新颖的Large-Margin softmax loss（L-softmax loss）。Large-Margin softmax loss来自ICML2016的论文：Large-Margin Softmax Loss for Convolutional Neural Networks 论文链接：htthttps://blog.csdn.net/u014380165/article/details/76864572?spm=1001.2014.3001.5501卷积神经网络系列之softmax，softmax loss和cross entropy的讲解_AI之路-CSDN博客_卷积神经网络softmax层我们知道卷积神经网络（CNN）在图像领域的应用已经非常广泛了，一般一个CNN网络主要包含卷积层，池化层（pooling），全连接层，损失层等。虽然现在已经开源了很多深度学习框架（比如MxNet，Caffe等），训练一个模型变得非常简单，但是你对这些层具体是怎么实现的了解吗？你对softmax，softmax loss，cross entropy了解吗？相信很多人不一定清楚。虽然网上的资料很多，但是...https://blog.csdn.net/u014380165/article/details/77284921?spm=1001.2014.3001.5501

large-margin softmax loss for convolutional neural networks这篇文章算的上是人脸识别方向的开箱之作了，后续有sphereface,cosface,arcface等等，改进softmax loss实际上是非常有意义的任务，在日常工作中，除了多标签分类任务（sigmoid），几乎所有的任务用的都是softmax loss。本文即是从loss角度上让model学一个更难的边界，在余弦距离上，让类和类之间强行多一个m，这样的话，类和类之间的距离会变得更大，类内的距离则变小。（encourages intra-class compactnessand inter-class separability between learned features.）

1.Introduction 

        上图很直观，softmax loss包括三部分，第一是输出特征维度的linear层，这里面包括了输入的x和特征权重w，其次是softmax函数，最后是交叉熵（如果交叉熵中用的是softmax，即是我们最常见的softmax cross-entropy loss）.current softmax loss does not explicitly encourage intra-class compactness and inter-class-separability.当前的softmax loss并没有鼓励类内紧凑型和类间可分性。怎么办？Our key intuition is that the separability between sample and parameter can be factorized into amplitude ones and angular ones with cosine similarity:作者直观就是将样本和参数之间可分性分解为具有余弦相似性的振幅和角度，即

w就是linear层的权重，x是linear层的特征输入，Under softmax loss,the label prediction decision rule is largely determined by the angular similarity to each class since softmax loss uses cosine distance as classification score. 由于softmax loss使用余弦距离作为分类分数，标签预测决策规则在很大程度上取决于每个类别的角度相似性。将softmax推广到large-margin softmax loss，margin可以理解成角度上的一个常量。

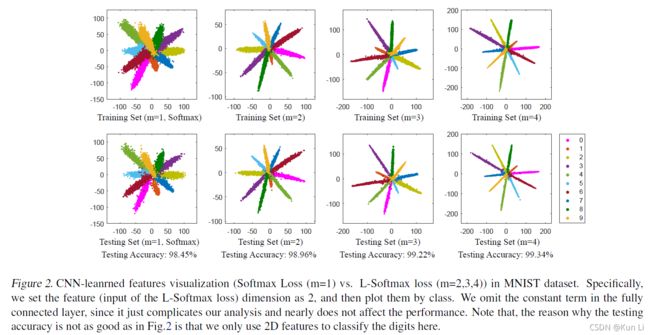
 使用不同的m值，类间距离确实分离了，类间也变得更加紧凑了。

2.related work and preliminaries

标准的softmax loss

 f就是linear层的输出，不过这层输出大小是负无穷到正无穷

        上面这个式子就使用向量乘法做了分解。其实也好理解为什么在这层做文章？softmax函数和交叉熵其实都不是和特征之间相关的因素，model从图像中学到的类间类内的特征才是最终给到loss去驱动的，因此在linear层中转成cos角度其实是loss驱动model去学更好特征的入口。

3.large-margin softmax loss

考虑一个二分类，并且样本x属于类别1：则希望softmax强制

However, we want to make the classification more rigorous in order to produce a decision margin. 作者希望分类更加严格，易产生决策margin。

      这里是整个文章最核心的点，cos单调递减，标签1的话就要求，预测的cos(角1)>cos(角2)(余弦距离)，cos(角1)>cos(m*角1)>cos(角2)，m值越大，意味着loss侧角1和角2的预测值变得更接近了，对于model来说，更难学了，loss这么设计是希望让类间的距离变得更大，大到两者之间隔了个m，So the new classification criteria is a stronger requirement to correctly classify x, producing a more rigorous decision boundary for class 1.新的分类loss对正确分类样本x提出了更高的要求，为类别1产生了一个更严格的决策边界。

        则l-softmax变成了：

        注意这个和角度相关的函数定义是一个分段函数，cos在0-π之间是单调递减的， 其中m是与分类边距密切相关的整数。m越大，分类间隔越大，学习目标也越难实现。同时，要求D是单调递减函数，D()应等于cos()。

最后看一下几何解释：

 可以看到中间这个decision margin还是很大的。

因此L-softmax loss的思想简单讲就是加大了原来softmax loss的学习难度。l-softmax希望类和类之前的余弦距离至少要在一个m倍以上，关于这个m就有很多可以做的文章了。