《python深度学习》笔记(六):二分类问题
二分类问题可能是应用最广泛的机器学习问题,它指的是所有数据的标签就只有两种,正面或者负面。在这个例子中,我们学习根据电影评论的文字内容将其划分为正面或者负面。
数据集介绍:
本节使用IMDB数据集,它包含来自互联网电影数据库(IMDB)的50000条严重两极分化
的评论。数据集被分为用于训练的25000条评论和用于测试的25000条评论,训练集和测试集都包含50%的正面评论和50%的负面评论。
为什么要将训练集和测试集分开?
因为你不应该将训练机器学习模型的同一批数据再用于测试模型!模型在训练数据上的表现很好,并不意味着它在前所未见的数据上也会变现得很好,我们真正关心的模型在新数据上的性能(因为已经知道了训练数据对应的标签,显然不再需要模型来进行预测)。例如,模型最终可能只是记住了训练样本和目标值之间的映射关系,但这对在前所未见的数据上进行预测毫无用处。
第一步:加载数据集
# 第一步:加载数据集
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
# num_word=10000表示仅保留训练数据前10000个最常见的出现的单词。低频单词舍弃,便于数据处理
# 标签都是由0和1组成的数据列表,其中0代表负面,1代表正面
# train_data和test_data都是评论组成的列表,每条评论又是单词组成的列表第二步:数据预处理
不能将整数序列直接输入神经网络。需要将列表转换为张量。转换方式有一下两种:
(1)填充列表,使其具有相同的长度,再将列表转换成形状为(samples, word_indices)的整数张量,然后网络第一层使用能处理这种整数张量的层(即Embedding层,以后写到关于Embedding层时再在这里放上链接)。
(2)对列表进行one-hot编码,将其转换为0和1组成的向量。举个例子,序列[3, 5]将会被转换为10000维向量,只有索引为3和5的元素是1,其余都是0。然后网络第一层可以用Dense层,它能够处理浮点数向量数据。
下面用第二种方法将数据向量化:
# 第二步:输入数据,数据编码
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension)) # 创建一个零矩阵
for i, sequence in enumerate(sequences): # 自动将列表中的元素按顺序编号
results[i, sequence] = 1
return results
# 将数据向量化
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data) # 数据向量化,使其转换为0和1组成的向量
# 标签向量化
y_test = np.asarray(test_labels).astype('float32')
y_train = np.asarray(train_labels).astype('float32') # 将图像标签数据转换为矩阵形式,把整数变成浮点数第三步:构建并编译模型
网络使用带有relu激活层的全连接层(Dense)的简单堆叠,最后一层用sigmoid来激活以输出一个0~1范围的概率值
对于这种Dense层的堆叠,需要确定以下两个关键架构:
(1)网络有多少层;
(2)每层有多少个隐藏单元。
下面搭建起来的网络模型的架构为:
(1)网路有两个中间层,每层都有16个隐藏单元;
(2)第三层输出一个标量,预测当前评论的情感。
传入Dense层的参数(16)是该层隐含单元的个数。一个隐藏单元是该层表示空间的一个维度。16个隐藏单元对应的权重矩阵W的形状为(input_dimension, 16)。隐藏单元越多(即更高维的表示空间),网络越能学到更加复杂的表示,但网络的计算代价也变得更大,而且可能会导致学到不好的模式(这种模式会提高训练数据上的性能,但不会提高测试数据上的性能)。
最后需要选择一个损失函数和优化器。面对二分类问题,网络的输出是一个概率值。网络最后一层使用sigmoid激活函数,仅包含一个单元,最好使用binary_crossentropy(二元交叉熵)损失。
# 第三步:构建网络模型
model = models.Sequential() # 线性堆叠
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu')) # 将所有负值归零
model.add(layers.Dense(1, activation='sigmoid')) # 将任意值压缩到0~1之间
"""
model.compile(optimizer='rmsprop',
loss='binary_crossentropy', # 二元交叉熵损失函数
metrics=['acc'])
# 自定义优化器和损失函数,自定义需要提前导入相应的部分
"""
model.compile(optimizer=optimizers.RMSprop(0.001), # 均方根误差优化器
loss='binary_crossentropy', # 二元交叉熵损失函数
metrics=['acc'])第四步:留出验证集
# 第四步:留出验证集
x_val = x_train[:10000] # 前面10000个数据
partial_x_train = x_train[10000:] # 10000到最后一个,剩下的所有
y_val = y_train[:10000]
partial_y_train = y_train[10000:]第五步:训练模型
注意,调用model.fit()返回了一个History对象,这个对象有一个history成员,它是一个字典,包含训练过程中的所有数据。
# 第五步:训练模型
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))第六步:绘制图像
# 绘制图像
history_dict = history.history # history 包含了训练过程中的所有数组。
# fit返回了一个对象hisrory,这个对象里包含了history,它是一个字典,包含训练数据中的所有数据。{‘acc':'86%','loss':’‘。。。}
loss_values = history_dict['loss'] # 训练损失
val_loss_values = history_dict['val_loss'] # 验证损失
epochs = range(1, len(loss_values)+1) # len(loss_values)表示损失值的个数,训练周期从1到20,range(1,21).
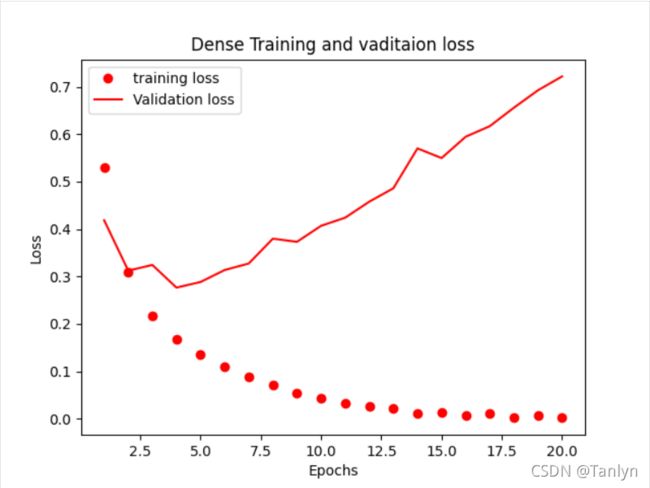
plt.plot(epochs, loss_values, 'ro', label='training loss')
plt.plot(epochs, val_loss_values, 'r', label='Validation loss')
plt.title('Dense Training and vaditaion loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend() # 用于给图像加图例
plt.show()
# 绘制训练精度和验证精度
plt.clf() # 清空图像
acc = history_dict['acc']
val_acc = history_dict['val_acc']
plt.plot(epochs, acc, 'go', label='Training Acc') # 'bo'表示蓝色圆点
plt.plot(epochs, val_acc, 'g', label='Validation Acc') # 'b'表示蓝色实线
plt.title('Dense Training and Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend() # 用于给图像加图例
plt.show() 从这个例子可以学到:
(1)通常要对原始数据进行大量预处理,以便将其转换为张量输入到神经网络中。单词序列可以编码为二进制向量,但也有其他编码方式。
(2)带有relu激活的Dense层堆叠,可以解决很多种问题(包括情感分类),你可能会经常用到这种模型。
(3)对于二分类问题,网络的最后一层应该是只有一个单元并使用sigmoid激活的Dense层;网络输出应该是0~1范围的标量,表示概念值;损失函数应该是binary_crossentropy损失函数。
(4)无论问题是什么,rmsprop优化器通常都是足够好的选择。
(5)随着神经网络在训练数据上的表现越来越好,模型最终会过拟合,并在前所未见的数据上得到越来越差的结果。一定要监控模型在训练集之外的数据集上的性能。