数据挖掘（一）使用 Apriori 算法进行关联分析

数据挖掘（一）使用 Apriori 算法进行关联分析

1.关联分析

关联分析是一种在大规模数据集中寻找有趣关系的任务。
这些关系可以有两种形式:

• 频繁项集（frequent item sets）: 经常出现在一块的物品的集合。
• 关联规则（associational rules）: 暗示两种物品之间可能存在很强的关系。

2.相关术语

• 关联分析（关联规则学习): 从大规模数据集中寻找物品间的隐含关系被称作 关联分析(associati analysis) 或者 关联规则学习（association rule learning） 。
  下面是用一个 杂货店 例子来说明这两个概念，如下图所示:
  
• 频繁项集: {葡萄酒, 尿布, 豆奶} 就是一个频繁项集的例子。
• 关联规则: 尿布 -> 葡萄酒 就是一个关联规则。这意味着如果顾客买了尿布，那么他很可能会买葡萄酒。

那么 频繁 的定义是什么呢？怎么样才算频繁呢？
度量它们的方法有很多种，这里我们来简单的介绍下支持度和可信度。

• 支持度: 数据集中包含该项集的记录所占的比例。例如上图中，{豆奶} 的支持度为 4/5。{豆奶, 尿布} 的支持度为 3/5。
• 可信度: 针对一条诸如 {尿布} -> {葡萄酒} 这样具体的关联规则来定义的。这条规则的 可信度 被定义为 支持度({尿布, 葡萄酒})/支持度({尿布})，从图中可以看出 支持度({尿布, 葡萄酒}) = 3/5，支持度({尿布}) = 4/5，所以 {尿布} -> {葡萄酒} 的可信度 = 3/5 / 4/5 = 3/4 = 0.75。

支持度 和 可信度 是用来量化 关联分析 是否成功的一个方法。
假设想找到支持度大于 0.8 的所有项集，应该如何去做呢？
一个办法是生成一个物品所有可能组合的清单，然后对每一种组合统计它出现的频繁程度，但是当物品成千上万时，上述做法就非常非常慢了。
我们需要详细分析下这种情况并讨论下 Apriori 原理，该原理会减少关联规则学习时所需的计算量。

• 频繁项集: {葡萄酒, 尿布, 豆奶} 就是一个频繁项集的例子。
• 关联规则: 尿布 -> 葡萄酒 就是一个关联规则。这意味着如果顾客买了尿布，那么他很可能会买葡萄酒。

那么 频繁 的定义是什么呢？怎么样才算频繁呢？
度量它们的方法有很多种，这里我们来简单的介绍下支持度和可信度。

• 支持度: 数据集中包含该项集的记录所占的比例。例如上图中，{豆奶} 的支持度为 4/5。{豆奶, 尿布} 的支持度为 3/5。
• 可信度: 针对一条诸如 {尿布} -> {葡萄酒} 这样具体的关联规则来定义的。这条规则的 可信度 被定义为 支持度({尿布, 葡萄酒})/支持度({尿布})，从图中可以看出 支持度({尿布, 葡萄酒}) = 3/5，支持度({尿布}) = 4/5，所以 {尿布} -> {葡萄酒} 的可信度 = 3/5 / 4/5 = 3/4 = 0.75。
  
  支持度 和 可信度 是用来量化 关联分析 是否成功的一个方法。
  假设想找到支持度大于 0.8 的所有项集，应该如何去做呢？
  一个办法是生成一个物品所有可能组合的清单，然后对每一种组合统计它出现的频繁程度，但是当物品成千上万时，上述做法就非常非常慢了。
  我们需要详细分析下这种情况并讨论下 Apriori 原理，该原理会减少关联规则学习时所需的计算量。

3.Apriori 原理

假设我们一共有 4 个商品: 商品0, 商品1, 商品2, 商品3。
所有可能的情况如下:

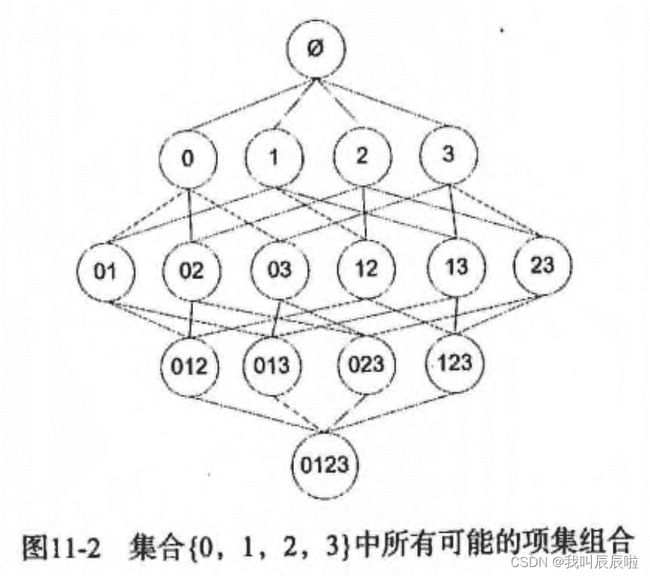
如果我们计算所有组合的支持度，也需要计算 15 次。即 2^N - 1 = 2^4 - 1 = 15。
随着物品的增加，计算的次数呈指数的形式增长 …
为了降低计算次数和时间，研究人员发现了一种所谓的 Apriori 原理，即某个项集是频繁的，那么它的所有子集也是频繁的。
例如，如果 {0, 1} 是频繁的，那么 {0}, {1} 也是频繁的。
该原理直观上没有什么帮助，但是如果反过来看就有用了，也就是说如果一个项集是 非频繁项集，那么它的所有超集也是非频繁项集，如下图所示:

在图中我们可以看到，已知灰色部分 {2,3} 是 非频繁项集，那么利用上面的知识，我们就可以知道 {0,2,3} {1,2,3} {0,1,2,3} 都是 非频繁的。
也就是说，计算出 {2,3} 的支持度，知道它是 非频繁 的之后，就不需要再计算 {0,2,3} {1,2,3} {0,1,2,3} 的支持度，因为我们知道这些集合不会满足我们的要求。
使用该原理就可以避免项集数目的指数增长，从而在合理的时间内计算出频繁项集。

Apriori 算法优缺点

* 优点: 易编码实现
* 缺点: 在大数据集上可能较慢
* 适用数据类型: 数值型 或者 标称型数据。

Apriori 算法流程步骤:

* 收集数据: 使用任意方法。
* 准备数据: 任何数据类型都可以，因为我们只保存集合。
* 分析数据: 使用任意方法。
* 训练数据: 使用Apiori算法来找到频繁项集。
* 测试算法: 不需要测试过程。
* 使用算法: 用于发现频繁项集以及物品之间的关联规则。

4.Apriori 算法的使用

前面提到，关联分析的目标包括两项: 发现 频繁项集 和发现 关联规则。
首先需要找到 频繁项集，然后才能发现 关联规则。
Apriori 算法是发现 频繁项集 的一种方法。
Apriori 算法的两个输入参数分别是最小支持度和数据集。
该算法首先会生成所有单个物品的项集列表。
接着扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度要求的集合会被去掉。
燃尽后对生下来的集合进行组合以声场包含两个元素的项集。
接下来再重新扫描交易记录，去掉不满足最小支持度的项集。
该过程重复进行直到所有项集被去掉。




使用apriori包中apyori函数实现apriori关联度规则挖掘：

# 输入数据集
input=[['I1','I2','I5'],
['I1','I2'],
['I2','I4'],
['I1','I2','I4'],
['I1','I3'],
['I1','I2','I3','I5'],
['I1','I2','I3'],
['I2','I5'],
['I2','I3','I4'],
['I3','I4']]

# 使用apriori包中apyori函数实现apriori关联度规则挖掘
from apyori import apriori
import pandas as pd

result = list(apriori(transactions=input,min_support=0.2,min_confidence = 0.8))

result = pd.DataFrame(result)
print(result)

5.总结

Apriori是一种常用的数据关联规则挖掘方法，它可以用来找出数据集中频繁出现的数据集合。找出这样的一些频繁集合有利于决策，例如通过找出超市购物车数据的频繁项集，可以更好地设计货架的摆放。

Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准（置信度or提升度）的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集AB和ABE，那么我们会抛弃AB，只保留ABE，因为AB是2项频繁集，而ABE是3项频繁集。

主要思想是通过一层一层的递归搜索，通过第k层的频繁项集，利用简单的剪枝远离推算出第k+1层的候选集，然后通过对数据集的扫描，计算出真正的频繁项集。其中主要用到两个剪枝的基本原理：如果某个项集是频繁的，意味着它全部子集也是和它一样的频繁项集的。与之相对的，如果一个项集是非频繁项集，那么所有包括它的集合也不是频繁项集。

Apriori算法最大的优点是设计虽然简单但完整，逻辑比较清晰，泛用性广，能够很好的进行扩展。例如其能够支持分布式的开发区与增量式计算。性能上来说，相比纯粹的暴力枚举算法有了很大的进步，已经能够进行小规模的关联规则分析了，但是当面对较复杂的情况，例如数据集较大，或者基本项目较大且最小支持度较小时。算法性能就会捉襟见肘了。

算法性能分析分为两个部分。
生成候选项集apriori_gen：这里的性能主要取决于上一层的频繁项集个数，这将决定着这个部分需要的时间，大概时间复杂度是：nnk*log(k)。
计算频繁项集scan_total：上一步生成的候选项集将决定这一部分的的遍历次数。也就决定了这一部分运行所需要的时间，所以尽可能生成少的候选项集是非常关键的。

综上所述，当数据量变多和项目数量变多时，算法的时间复杂度将会以非常恐怖的速度增长。这将是计算机不可承受的。为了降低时间复杂度，尽可能的减少对数据集的扫描。于是诞生了FP-Growth算法，通过将所有事务数据建成一颗FP-tree。提高计算频繁项集的速度。