学习官方PyG文档

---

前言

随着与深度学习火热，选择一款框架会使我们学习和使用更加方便（尤其是对初学者而言——我）我对比了两大框架DGL、PyG。最终选择了PyG，理由是因为教程多，可以搜到比较全面的教程。DGL我也很喜欢，很简洁但无奈教程视频太少导致我无从下手：

随着图深度学习的不断发展，图机器学习这门技术也越来越流行，很多人都开启了学习机器学习，它在各个领域都能有自己的发挥（生物医疗，自然语言，图像处理），我是学生物的所以一眼就爱上了图神经网络，我就觉得图神经网络就是为化合物小分子、蛋白而生。

---

一、PyG安装

安装很简单建议用Anaconda或者Miniconda安装，PyG现在可以通过Anaconda为MAC/Windows/Linux一键安装（要求Pytorch >= 1.8.0）。

conda install pyg -c pyg

其他的办法我没有试，我就喜欢换简简单单的安装，方方便便的使用。

二、PyG快速入门（理解）

1.PyG的主要功能：

• 图形的数据处理
• PyG包装的数据集
• 小批量图形
• 数据转换
• 图学习算法
• 课后题（加深巩固理解）

图形的数据处理

图形是被用来模拟节点与边的配对关系，PyG中单个图的构建是由torch_geometric.data.Data构建的,它默认的属性有：

• data.x:节点特征矩阵，矩阵的形状[N,M]，(N节点的数量,M节点特征的数量)。
• data.edge_index:COO格式（不明白的可以参考）的图形连接，形状[2,E]数值类型为(torch.long)，E是边的数量。
• data.edge_attr:边的特征矩阵，形状为[E,K]，K为边特征的数量。
• data.y:要训练的目标（可能具有任意的形状）。（我理解的可能就是如果是二分类就是0 or 1，回归可能就是连续值。）
• data.pos:节点的位置矩阵，形状[N,D]，D是维度。如果坐标是2-D，那就是D=2，3-D就是D=3。（我是这么认为的）

其实上面的属性我们并不是都能用得到，也并不局限以上的属性。也就是说我们可以扩展。

如何将数据转化为图数据？

import torch
from torch_geometric.data import Data
import networkx as nx
from torch_geometric.utils.convert import to_networkx

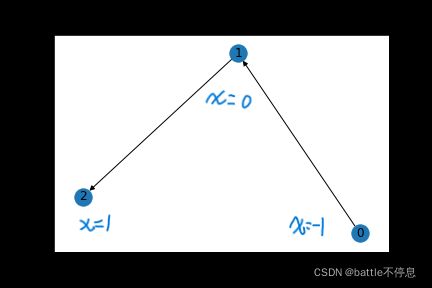
###这是有向图0->1,1->2
edge_index = torch.tensor([[0, 1 ],
                           [1, 2 ]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)

data = Data(x=x, edge_index=edge_index)
G = to_networkx(data)
nx.draw_networkx(G)

##双向图也即是无向图，在创建边时候要重复添加相反方向的边。
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)

data = Data(x=x, edge_index=edge_index)
G = to_networkx(data)
nx.draw_networkx(G)

注意：再用PyG构建图边的图形连接时，edge_index的形状必须时[2,E]。如果不是要记得转化一下。

import torch
from torch_geometric.data import Data

edge_index = torch.tensor([[0, 1],
                           [1, 0],
                           [1, 2],
                           [2, 1]], dtype=torch.long)
###edge_index.shape == [4,2],所以在下面构建的时候需要转置一下变为[2,E]
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)

data = Data(x=x, edge_index=edge_index.t().contiguous())

在构建模型的时候可以时常打印一下数组的形状，进行查看和检查。

print(data.keys)
print(data['x'])
for key, item in data:
    print(f'{key} found in data')
print(data.num_nodes)
print(data.num_edges)
print(data.num_node_features)

输出
['x', 'edge_index']
tensor([[-1.],
        [ 0.],
        [ 1.]])
x found in data
edge_index found in data
节点数量 3
边的数量 4
节点特征数量 1

PyG包装的的数据集

PyG包含大量常见的基准数据集，例如，所有Planetoid数据集（Cora，Citeseer，Pubmed），http://graphkernels.cs.tu-dortmund.de 及其清理版本的所有图形分类数据集，QM7和QM9数据集，以及一些3D网格/点云数据集，如FAUST，ModelNet10/40和ShapeNet。

初始化数据集很简单。数据集的初始化将自动下载其原始文件并将其处理为先前描述的数据格式。例如，要加载 ENZYMES 数据集（由 6 个类中的 600 个图组成）：

from torch_geometric.datasets import TUDataset

dataset = TUDataset(root='./ENZYMES', name='ENZYMES')
print('数据集的长度:',len(dataset))
print('数据的分类数:',dataset.num_classes)
print('数据的节点特征数:',dataset.num_node_features)
print('图的构造:',dataset[0])
print(data.is_directed()) ## 是否为有向图
print(data.is_undirected()) ##True 是否为无向图

输出
ENZYMES(600)
数据集的长度: 600
数据的分类数: 6
数据的节点特征数: 3
图的构造: Data(edge_index=[2, 168], x=[37, 3], y=[1])
False

我们可以看到每一个图包含了37个节点，每个节点三个特征。此数据集是分类数据集，共有6个类别，且每个图都是无向图，无向边的数量为168/2=84,y=[1],说明这个图是1类别。
数据集可以通过类似于列表的切片、布尔张量来分割数据集。

train_dataset = dataset[:540]
test_dataset = dataset[540:]
print(train_dataset)
print(test_dataset)

输出
ENZYMES(540)
ENZYMES(60)

如果您不确定数据集在拆分之前是否已经打乱，您可以通过运行随机排列它，

dataset = dataset.shuffle()
输出
>ENZYMES(600)

我们试一下另一个数据，让我们下载用于半监督图节点分类的标准基准数据集 Cora：

from torch_geometric.datasets import Planetoid

dataset = Planetoid(root='./Cora', name='Cora')
print(dataset)
print(dataset.num_classes)
print(dataset.num_node_features)
输出
>Core()
>1
>7
>1433

data = dataset[0]
print(data)
print(data.is_undirected())
print(data.train_mask.sum().item()) ## 140个节点训练
print(data.val_mask.sum().item()) ## 500个节点验证
print(data.test_mask.sum().item()) ## 1000个节点测试

输出
Data(x=[2708, 1433], edge_index=[2, 10556], y=[2708], train_mask=[2708], val_mask=[2708], test_mask=[2708])
True
140
500
1000

批量图

神经网络通常以批量方式进行训练。 PyG 通过创建稀疏块对角邻接矩阵，并在节点维度中连接特征和目标矩阵来实现小批量的并行化。这种组合允许在一批中的示例上使用不同数量的节点和边。

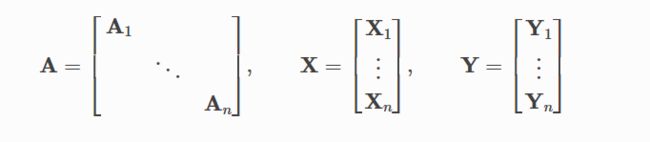
PyG 包含自己的 torch_geometric.loader.DataLoader，它已经处理了这个连接过程。

from torch_geometric.datasets import TUDataset
from torch_geometric.loader import DataLoader

dataset = TUDataset(root='./ENZYMES', name='ENZYMES', use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)

for batch in loader:
    print(batch,'--num_graph:',batch.num_graphs)

输出
DataBatch(edge_index=[2, 3830], x=[989, 21], y=[32], batch=[989], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3894], x=[991, 21], y=[32], batch=[991], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3898], x=[1053, 21], y=[32], batch=[1053], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3904], x=[1056, 21], y=[32], batch=[1056], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 4370], x=[1112, 21], y=[32], batch=[1112], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3842], x=[964, 21], y=[32], batch=[964], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 4160], x=[1175, 21], y=[32], batch=[1175], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3908], x=[1002, 21], y=[32], batch=[1002], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3994], x=[1055, 21], y=[32], batch=[1055], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 4026], x=[1026, 21], y=[32], batch=[1026], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3838], x=[993, 21], y=[32], batch=[993], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 4268], x=[1125, 21], y=[32], batch=[1125], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3872], x=[995, 21], y=[32], batch=[995], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 4200], x=[1087, 21], y=[32], batch=[1087], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3810], x=[1072, 21], y=[32], batch=[1072], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3774], x=[976, 21], y=[32], batch=[976], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 4026], x=[1069, 21], y=[32], batch=[1069], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3820], x=[1022, 21], y=[32], batch=[1022], ptr=[33]) --num_graph: 32
DataBatch(edge_index=[2, 3130], x=[818, 21], y=[24], batch=[818], ptr=[25]) --num_graph: 24

最后一个batch是24个图，Dataloader默认是最后剩余多少就作为一个batch输出多少。
我们可以使用batch来为每个图单独计算节点维度中的平均节点特征。

from torch_scatter import scatter_mean
from torch_geometric.datasets import TUDataset
from torch_geometric.loader import DataLoader

dataset = TUDataset(root='./ENZYMES', name='ENZYMES', use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)

for data in loader:
    print(data.num_graphs)
    
    x = scatter_mean(data.x,data.batch,dim=0)
    print(x.size())
    break

#for data in loader:
#    print(data.x)
#    print(data.batch)
#    break

输出
32
torch.Size([32, 21])

理解 torch_scaterr.scatter_mean()

torch_scatter.scatter_mean(src,index,dim=-1,out=None,dim_size=None,fill_value=0)
#将张量的所有值平均到沿给定轴在张量中指定的索引处。如果多个指数引用同一位置，则其将其平均后放入指定位置。

图片来自：torch_scatter文档

数据转换

变换是变换图像和执行增强的常用方法。PyG 带有自己的转换，它期望一个 Data 对象作为输入并返回一个新的转换后的 Data 对象。可以使用 torch_geometric.transforms.Compose 将变换连接在一起，并在将处理后的数据集保存到磁盘或访问数据集中的图形之前应用 。
我们在 ShapeNet 数据集（包含 17,000 个 3D 形状点和 16 个形状类别的每个点标签）上应用变换。

import torch_geometric.transforms as T
from torch_geometric.datasets import ShapeNet

dataset = ShapeNet(root='/tmp/ShapeNet', categories=['Airplane'],
                    pre_transform=T.KNNGraph(k=6))

dataset[0]

输出
Data(pos=[2518, 3], y=[2518])

转换：

import torch_geometric.transforms as T
from torch_geometric.datasets import ShapeNet

dataset = ShapeNet(root='./ShapeNet', categories=['Airplane'],
                    pre_transform=T.KNNGraph(k=6))

dataset[0]
print(dataset[0].pos)

输出
Data(edge_index=[2, 15108], pos=[2518, 3], y=[2518])
tensor([[-0.0145, -0.0164,  0.0320],
        [-0.0119, -0.0657,  0.0145],
        [-0.1424, -0.0370, -0.0519],
        ...,
        [ 0.0342, -0.0931, -0.0523],
        [-0.0108, -0.0600,  0.0522],
        [-0.0165, -0.0593,  0.0560]])

此外，我们可以使用参数来随机增加一个 Data 对象，例如，将每个节点位置平移一个小数字：

import torch_geometric.transforms as T
from torch_geometric.datasets import ShapeNet

dataset = ShapeNet(root='./ShapeNet', categories=['Airplane'],
                    pre_transform=T.KNNGraph(k=6),
                    transform=T.RandomTranslate(0.01)# 节点位置平移)

dataset[0]
print(dataset[0].pos)

输出
Data(edge_index=[2, 15108], pos=[2518, 3], y=[2518])
tensor([[-0.0225, -0.0091,  0.0257],
        [-0.0181, -0.0687,  0.0093],
        [-0.1331, -0.0440, -0.0549],
        ...,
        [ 0.0423, -0.1002, -0.0472],
        [-0.0206, -0.0615,  0.0602],
        [-0.0250, -0.0632,  0.0545]])

通过与上面没有进行RandomTranslate操作的位置pos矩阵比较，会发现有不同。

图学习算法

在了解了 PyG 中的数据处理、数据集、加载器和转换之后，我们就可以实现第一个较为简单理解的图神经网络了。
我们将使用一个简单的 GCN 层并在 Cora 引文数据集上复制实验。有关 GCN 的高级解释，请查看其博客。

##第一步导入必要的库
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid

##第二步导入数据集，或者建立自己的数据集
dataset = Planetoid(root='./Cora', name='Cora')
## 第三步建立模型
class GCN(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = GCNConv(dataset.num_node_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)
##第四步配置参数和模型
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = GCN().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
##第五步训练模型
model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    if epoch % 10 == 0:
        print('第{:4d}个eopch,\t loss:{:.4f}'.format(epoch+1,loss.item()))
##第六步验证
model.eval()
pred = model(data).argmax(dim=1)
correct = (pred[data.test_mask] == data.y[data.test_mask]).sum()
acc = int(correct) / int(data.test_mask.sum())
print(f'Accuracy: {acc:.4f}')

输出
第   1个eopch,	 loss:0.0136
第  11个eopch,	 loss:0.0184
第  21个eopch,	 loss:0.0123
第  31个eopch,	 loss:0.0414
第  41个eopch,	 loss:0.0114
第  51个eopch,	 loss:0.0073
第  61个eopch,	 loss:0.0304
第  71个eopch,	 loss:0.0132
第  81个eopch,	 loss:0.0245
第  91个eopch,	 loss:0.0220
第 101个eopch,	 loss:0.0215
第 111个eopch,	 loss:0.0187
第 121个eopch,	 loss:0.0070
第 131个eopch,	 loss:0.0282
第 141个eopch,	 loss:0.0197
第 151个eopch,	 loss:0.0105
第 161个eopch,	 loss:0.0235
第 171个eopch,	 loss:0.0193
第 181个eopch,	 loss:0.0167
第 191个eopch,	 loss:0.0199

模型验证
Accuracy: 0.8120

总结

以上代码均运行过，都可以跑的通。

1.edge_index.t().contiguous()的作用，通过pytorch建立图形，它只识别[2,E]形状的tensor。但是我们习惯建立[E,2]形状的tensor，所以要用edge_index.t().contiguous()转换一下。
2.我现在也不是很明白DataBatch(batch=[1082], edge_index=[2, 4066], x=[1082, 21], y=[32])中y到底是表示什么，但是好像不太耽误其他的理解。
这就算是基础入门PyG了，可以快乐的使用它进行建模了耶！
3.PyG文档