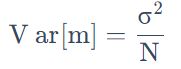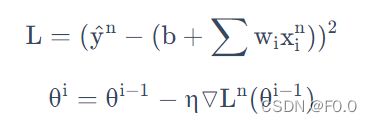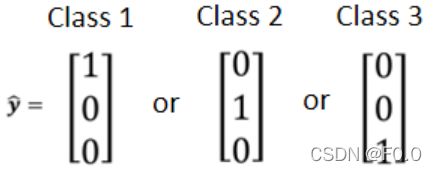李宏毅机器学习
目录
一、机器学习简介
1、机器学习流程
2、机器学习相关技术
二、回归
四、误差
4.1 偏差与方差
4.2 过拟合与欠拟合
4.3 交叉验证
4.4 N 折交叉验证
5. 梯度下降
5.1 调整学习速率
5.2 随机梯度下降
5.3 特征缩放
6 深度学习
6.1 神经网络
6.2 全连接前馈神经网络
6.3 神经网络本质
7 神经网络的训练
7.1 局部最小点与鞍点
7.1.1 如何判断
7.1.2 在鞍点确定参数更新方向
7.2 批次(Batch)和动量(Momentum)
7.2.1 Batch
7.2.2 Momentum
7.3自动调整学习速率（Learning Rate）
7.3.1 问题
7.3.2 求取σ的方式：Root Mean Square
7.3.3 RMSProp：调整“当前步”梯度与“历史”梯度的重要性
7.3.4 Learning Rate Scheduling：让LearningRate 与 “训练时间”有关
7.3.5 总结
7.4 分类（Classification）
7.4.1 Loss of Classifacation
7.5 批次标准化（Batch Normalization）
7.5.1 问题
7.5.2 解决方案：Feature Normalization(归一化)
7.5.3 Batch Normalization
7.5.4 还原
7.5.5 Testing
8 CNN
8.1 why cnn for image？
8.1.1 Small Region
8.1.2 Same Patterns
8.1.3 Subsampling（下采样）
8.2 ＣＮＮ－Convolution
８.２.１ Ｐｒｏｐｅｔｒｙ １
８.２.２ Ｐｒｏｐｅｔｒｙ ２
８.３ CNN－Ｃｏｌｏｒｆｕｌ Ｉｍａｇｅ
８.４ Convolution v.s Fully Connected
８.５CNN－Ｍａｘ Pooling
８.６ CNN－Ｆｌａｔｔｅｎ
８.７ CNN ｉｎ Ｋｅｒａｓ
一、机器学习简介
1、机器学习流程
左边的部分叫training，是学习的过程；右边的部分叫做testing，学好以后可以拿它做应用。在整个machine learning framework整个过程分成了三个步骤。第一个步骤就是找一个function，第二个步骤让machine可以衡量一个function是好还是不好，第三个步骤是让machine有一个自动的方法，有一个好演算法可以挑出最好的function。
2、机器学习相关技术
回归与分类：Regression和Classification的差别就是我们要机器输出的东西的类型是不一样。在Regression中机器输出的是一个数值，在Classification里面机器输出的是类别。假设Classification问题分成两种，一种叫做二分类输出的是是或否；另一类叫做多分类，在Multi-class中是让机器做一个选择题，等于是给他数个选项，每个选项都是一个类别，让他从数个类别里选择正确的类别。
监督学习：监督学习的问题是我们需要大量的training data。training data告诉我们要找的function的input和output之间的关系。如果我们在监督学习下进行学习，我们需要告诉机器function的input和output是什么。这个output往往没有办法用很自然的方式取得，需要人工的力量把它标注出来，这些function的output叫做label。
半监督学习：少量的labelled data，但是又有大量的Unlabeled data。
迁移学习：只有少量的有label的data。但是我们现在有大量的data，这些大量的data中可能有label也可能没有label。但是他跟我们现在要考虑的问题是没有什么特别的关系的。
无监督学习：完全没有任何labe
结构化学习：structured learning 中让机器输出的是要有结构性的，举例来说：在语音辨识里面，机器输入是声音讯号，输出是一个句子。句子是要很多词汇拼凑完成。它是一个有结构性的object。
强化学习：在reinforcement learning里面，我们没有告诉机器正确的答案是什么，机器所拥有的只有一个分数，就是他做的好还是不好。
二、回归
定义：找到一个函数，通过输入特征，输出一个数值。
模型步骤：模型假设、模型评估、模型优化
四、误差
4.1 偏差与方差
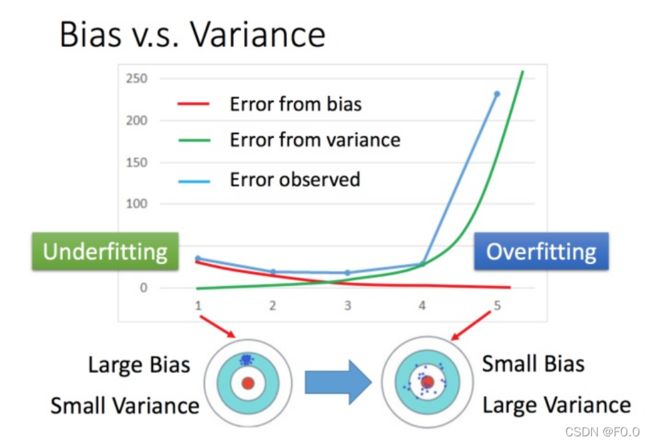
误差来源：偏差（Bias）、方差（Variance）
偏差 
方差 
不同模型的方差：一次模型的方差就比较小的，也就是比较集中，离散程度较小。而5次模型的方差就比较大。所以用比较简单的模型，方差是比较小的（就像射击的时候每次的时候，每次射击的设置都集中在一个比较小的区域内）。这也是因为简单的模型受到不同训练集的影响是比较小的。
不同模型的偏差：简单的模型函数集的space比较小，所以可能space里面就没有包含靶心，肯定射不中。而复杂的模型函数集的space比较大，可能就包含的靶心，只是没有办法找到确切的靶心在哪，但足够多的，就可能得到真正的 f¯。
偏差与方差：将误差拆分为偏差和方差。简单模型（左边）是偏差比较大造成的误差，这种情况叫做欠拟合，而复杂模型（右边）是方差过大造成的误差，这种情况叫做过拟合
4.2 过拟合与欠拟合
如果模型没有很好的训练训练集，就是偏差过大，也就是欠拟合。如果模型很好的训练训练集，即在训练集上得到很小的错误，但在测试集上得到大的错误，这意味着模型可能是方差比较大，就是过拟合。
欠拟合处理方法：重新设计模型
过拟合处理方法：更多的数据
4.3 交叉验证
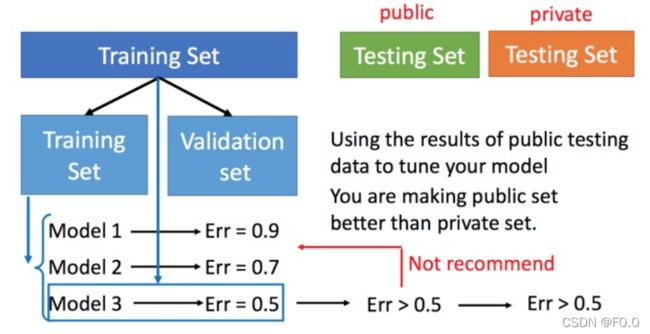
交叉验证就是将训练集再分为两部分，一部分作为训练集，一部分作为验证集。用训练集训练模型，然后再验证集上比较，确实出最好的模型之后（比如模型3），再用全部的训练集训练模型3，然后再用public的测试集进行测试，此时一般得到的错误都是大一些的。不过此时会比较想再回去调一下参数，调整模型，让在public的测试集上更好，但不太推荐这样。
4.4 N 折交叉验证
将训练集分成N份
比如在三份中训练结果Avg Err是模型1最好，再用全部训练集训练模型1。
5. 梯度下降
5.1 调整学习速率
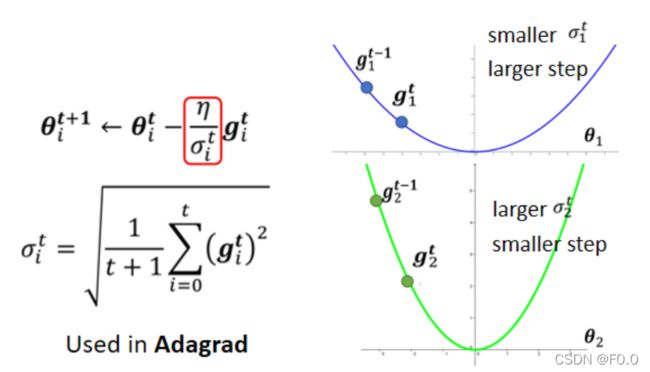
Adagrad算法：每个参数的学习率都把它除上之前微分的均方根。
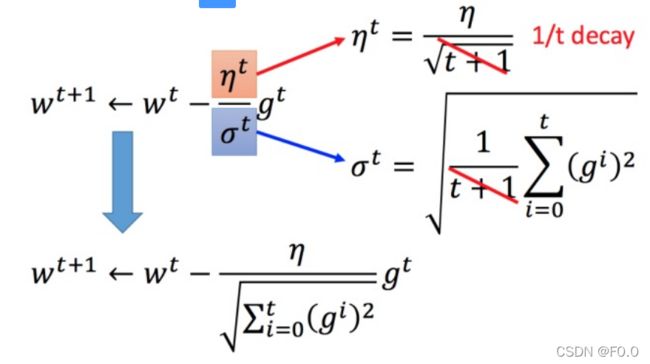
普通的梯度下降 Adagrad：σt :之前参数的所有微分的均方根，对 于每个参数都是不一样的。
将 Adagrad 的式子进行化简
最好的步伐应该是：
对于
就是希望再尽可能不增加过多运算的情况下模拟二次微分
5.2 随机梯度下降
普通梯度下降：
随机梯度下降：
随机梯度下降法更快，损失函数不需要处理训练集所有的数据。此时不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数Ln，就可以update 梯度。
5.3 特征缩放
坐标系中是两个参数的error surface（现在考虑左边蓝色），因为 w1 对 y 的变化影响比较小，所以 w1 对损失函数的影响比较小，w1 对损失函数有比较小的微分，所以 w1 方向上是比较平滑的。同理 x2 对 y 的影响比较大，所以x2 对损失函数的影响比较大，所以在x2 方向有比较尖的峡谷。
上图右边是两个参数scaling比较接近，右边的绿色图就比较接近圆形。
对于左边的情况，上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的，两个方向上需要不同的学习率，同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的，而是顺着等高线切线法线方向走的。但绿色就可以向着圆心（最低点）走，这样做参数更新也是比较有效率。
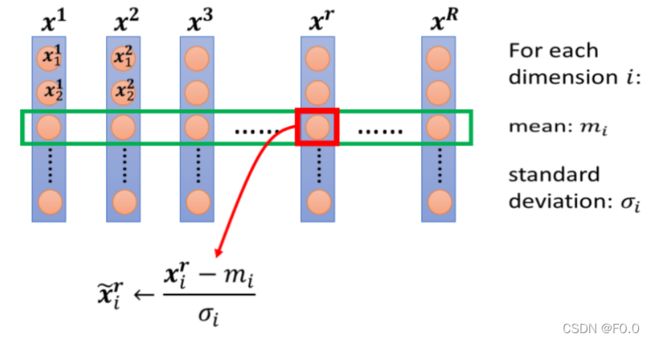
上图每一列都是一个例子，里面都有一组特征。
对每一个维度 i（绿色框）都计算平均数，记做 mi；还要计算标准差，记做 σi。
然后用第 rr个例子中的第 i个输入，减掉平均数 mi，然后除以标准差 σi，得到的结果是所有的维数都是 0，所有的方差都是 1
6 深度学习
三个步骤：神经网络、模型评估、选择最优函数
6.1 神经网络
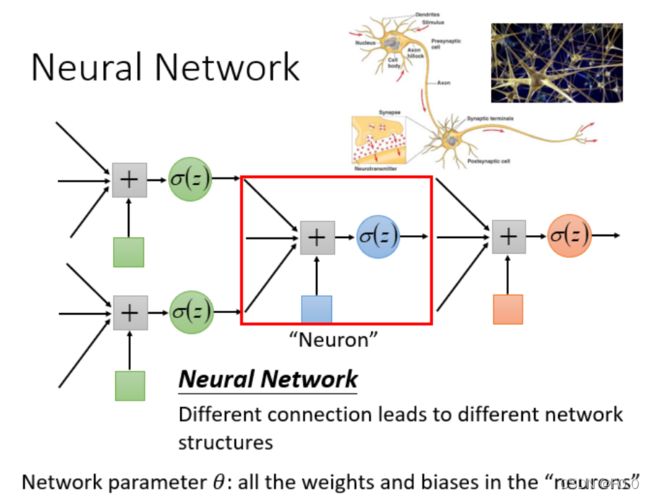
神经网络可以有很多不同的连接方式，这样就会产生不同的结构（structure）。在这个神经网络里面，我们有很多逻辑回归函数，其中每个逻辑回归都有自己的权重和自己的偏差，这些权重和偏差就是参数。
如果一个神经网络的权重和偏差已知，就可以看成一个函数，输入是一个向量，对应的输出也是一个向量。不论是做回归模型（linear model）还是逻辑回归（logistics regression）都是定义了一个函数集（function set）。我们可以给上面结构的参数设置为不同的数，就是不同的函数。这些可能的函数结合起来就是一个函数集。这时的函数集比较大，是以前的回归模型等没有办法包含的函数，所以说深度学习能表达出以前所不能表达的情况。
6.2 全连接前馈神经网络
输入层（Input Layer）：1层
隐藏层（Hidden Layer）：N层
输出层（Output Layer）：1层
因为layer1与layer2之间两两都有连接，所以叫做Fully Connect，因为现在传递的方向是由后往前传，所以叫做Feedforward。
6.3 神经网络本质
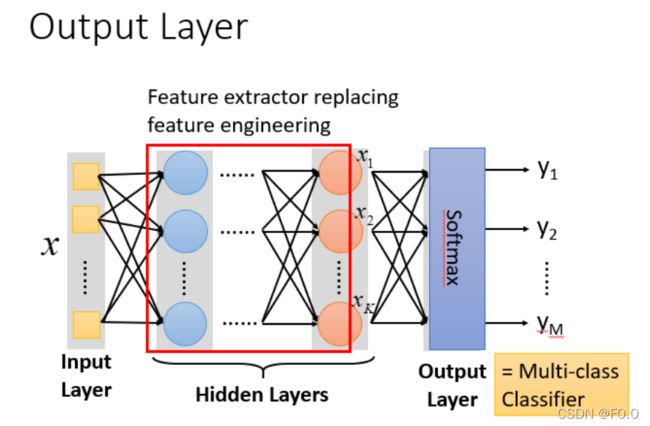
通过隐藏层进行特征转换：把隐藏层通过特征提取来替代原来的特征工程，这样在最后一个隐藏层输出的就是一组新的特征（相当于黑箱操作）。而对于输出层，其实是把前面的隐藏层的输出当做输入（经过特征提取得到的一组最好的特征）然后通过一个多分类器（可以是softmax函数）得到最后的输出y。
7 神经网络的训练
Optimization的时候,怎么把gradient descent做得更好。
7.1 局部最小点与鞍点
做Optimization时，随着参数不断更新，训练的loss不会再下降，是因为这时的参数对loss的微分为0。可能是因为卡在了局部最小点或鞍点。
7.1.1 如何判断
考察θ附近Loss的梯度→泰勒展开→海森矩阵
第一项中，当θ跟θ'很接近的时候，L(θ)和L(θ')很接近
第二项中，g代表梯度（一阶导数），可以弥补L(θ)与L(θ')之间的差距
第三项中，H表示海塞矩阵，是L的二阶导数
在Critical point附近时，第二项为0，根据第三项来判断→只需考察H的特征值
如果所有eigen value都是正的,H是positive definite （正定矩阵）,此时就是local minima；所有eigen value都是负的,H是negative definite,此时是local maxima；如果eigen value有正有负,那就代表是saddle point。
7.1.2 在鞍点确定参数更新方向
令特征值小于0，得到对应的特征向量u,在θ的位置加上u,沿著u的方向做update得到θ,就可以让loss变小。
注：Local Minima比Saddle Point少的多。
7.2 批次(Batch)和动量(Momentum)
7.2.1 Batch
在 Update 参数的时候,用B项样本数据出来算Loss和Gradient。所有的 Batch 看过一遍,叫做一个 Epoch。每个epoch开始前往往会重新分一次batch，每一个 Epoch 的 Batch 都不一样。
Small Batch v.s. Large Batch
考虑并行计算，大的BatchSize并不一定时间比较长。
因为有平行运算的能力,因此实际上,当Batch Size 小的时候，要跑完一个 Epoch,花的时间比大的 Batch Size 还要多的；反之，大的 Batch Size下，跑完一个Epoch花的时间反而是比较少的⇒Batch Size小时，Update的次数大大增加。
使用较小的BatchSize，在更新参数时会有Noisy⇒有利于训练。
使用较小的BatchSize,可以避免Overfitting⇒有利于测试(Testing)。
7.2.2 Momentum
Momentum是另外一个有可能可以对抗 Saddle Point 或 Local Minima 的技术。
一般的梯度下降，只考虑梯度的方向，向反方向移动
考虑动量的梯度下降：综合考虑梯度和前一步的方向
7.3自动调整学习速率（Learning Rate）
7.3.1 问题
1、 Training stuck ≠ Small Gradient：Loss不再下降时，未必说明此时到达Critical Point，梯度可能还很大。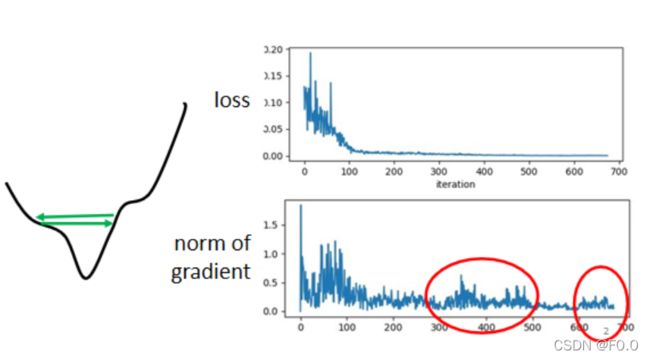
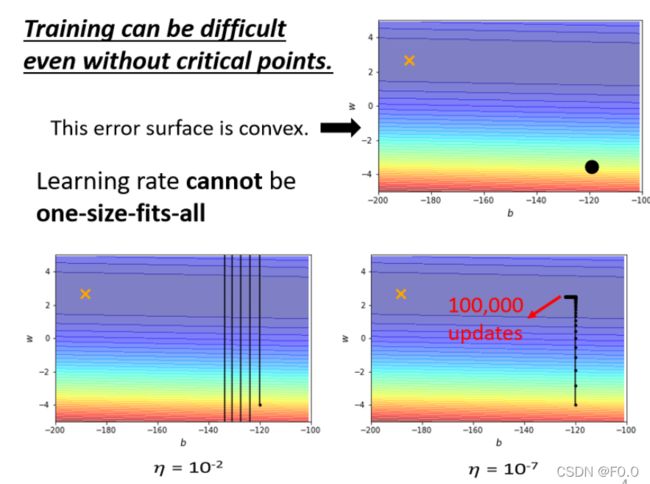
2、 如果使用“固定的”学习率，即使是在“凸面体”的优化，都会让优化的过程非常困难⇒客制化“学习率”⇒不同的参数（大小）需要不同的学习率
较大的学习率：Loss在山谷的两端震荡而不会下降
较小的学习率：梯度较小时几乎难以移动
客制化“梯度”⇒不同的参数（大小）需要不同的学习率
根据参数此时的实际情况，调整σ的大小，实现对参数θ的更新。
基本原则：
某一个方向上gradient的值很小,非常的平坦⇒learning rate调大一点；某一个方向上非常的陡峭,坡度很大⇒learning rate可以设得小一点
7.3.2 求取σ的方式：Root Mean Square
Adagrad（考虑之前所有梯度的大小）：对本次及之前计算出的所有梯度求均方根。
gradient都比较大,σ就比较大,在update的时候 参数update的量就比较小。
缺陷：不能“实时”考虑梯度的变化情况
7.3.3 RMSProp：调整“当前步”梯度与“历史”梯度的重要性
添加参数α，越大说明过去的梯度信息更重要
最常用的策略：Adam=RMSProp + Momentum
7.3.4 Learning Rate Scheduling：让LearningRate 与 “训练时间”有关
Learning Rate Scheduling：随著时间的不断地进行，随著参数不断的update，η越来越小
Warm Up：让learning rate先变大后变小
解释：σ指示某一个方向它到底有多陡/多平滑，这个统计的结果要足够多的数据才精准，一开始我们的统计是不精确的。所有一开始learning rate比较小，是让它探索收集一些有关error surface的情报，在这一阶段使用较小的learning rate，限制参数不会走的离初始的地方太远；等到σ统计得比较精准以后再让learning rate慢慢爬升。
7.3.5 总结
使用动量，考虑过去的梯度“正负”与“方向”
引入σ，考虑过去梯度的“大小”（RMS）
使用LearningRate Schedule
7.4 分类（Classification）
Class as one-hot vector
任何两个分类的距离都相同。
使用Softmax先把它们Normalize到0到1之间，这样才好跟 label 的计算相似度。
7.4.1 Loss of Classifacation
Cross-entropy比MSE更加适用于分类问题
7.5 批次标准化（Batch Normalization）
将Error Surface 铲平
7.5.1 问题
不同的参数发生变化，引起“损失函数”变化的程度不同⇒受“不同维度输入值的差异”的影响
- x1的值很小时，当参数w1有一个很小的变化，对y的影响很小，从而对Loss的影响也比较小。
- 反之，x2的值很大时，当参数w2有一个同样大小的变化，对y的影响则大得多，从而对Loss的影响也比较大。
因而，不同维度的输入值，大小的Scale差距很大，就可能产生在不同方向上，斜率、坡度非常不同的 error surface。
7.5.2 解决方案：Feature Normalization(归一化)
对不同数据样本向量的同一维进行归一化
做完 normalize 以后,这个 dimension 上面的数值就会平均是 0,然后它的 variance就会是 1，所以这一排数值的分布就都会在 0 上下；对每一个 dimension都做一样的 normalization，就会发现所有 feature 不同 dimension 的数值都在 0 上下，就制造出一个比较好的 error surface。
在深度学习中，每一层都需要一次Normalization。
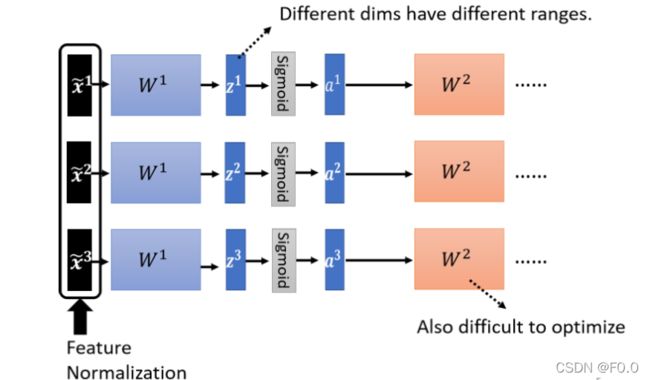
经过W1矩阵后，a 和 z数值的分布各维度仍然有很大的差异,要 train 第二层的参数W2也会有困难。需要对a或者z进行Normalization。如果选择的是 Sigmoid，比较推荐对 z 做 Feature Normalization,因为 Sigmoid 在 0 附近斜率比较大,如果对 z 做 Feature Normalization,把所有的值都挪到 0 附近，算 gradient 的时候,算出来的值会比较大。一般而言, normalization,要放在 activation function 之前或之后都是可以的。
步骤：
- 对向量的对应element做求平均、标准差的运算，求得向量μ，σ
- 对每个向z，利用μ，σ对对应element进行归一化，得到
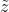
- 继续后续的步骤
7.5.3 Batch Normalization
实际上做Normalization时，只能考虑有限数量的数据⇒考虑一个Batch内的数据⇒近似整个数据集。
Batch Normalization适用于batch size 比较大时。其中data可以认为足以表示整个 corpus 的分布；从而，将对整个 corpus做 Feature Normalization 这件事情,改成只在一个 batch中做 Feature Normalization作为近似。
7.5.4 还原
引入向量γ，β，将原本被归一化到m=0，σ=1的各维度数据恢复到某一分布。
做 normalization 以后平均就一定是 0,可以视作是给 network 一些限制,也许这个限制会带来一些负面的影响，因而进行恢复操作，让模型自己学习γ，β。
训练时，初始将γ设为全为1的向量，β设为全为0的向量。在一开始训练的时候,让每一个 dimension 的分布比较接近。训练够长的一段时间,已经找到一个比较好的 error surface,走到一个比较好的地方以后,那再把γ，β 慢慢地加进去。
7.5.5 Testing
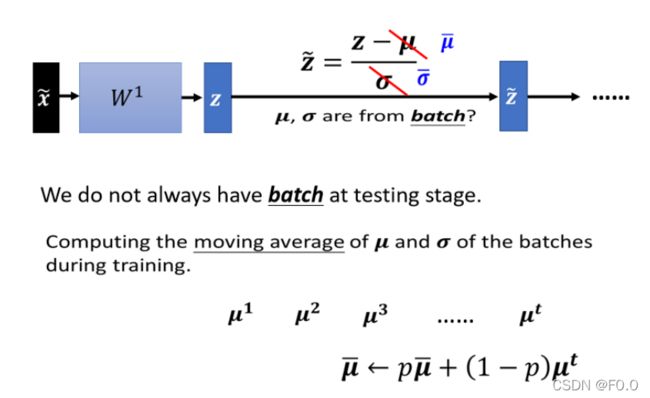
Testing 时没有Batch进行归一化⇒训练时会找到
在testing阶段，没有一个batch的数据，进行归一化。所以在 training 的时候，每一个 batch 计算出来的μ，σ ,都会拿出来算 moving average。
8 CNN
8.1 why cnn for image？
每一个neural代表一个最基本的分类器，使用全连接网络的话，100x100的彩色图片，拉成向量是100×100×3个像素，input vector假如是30000 dimension，hidden layer假设是1000个neural，那么这个hidden layer的参数就是有30000 *1000。
CNN的作用就是简化这个神经网络的结构，去掉一些用不到的weight。事实上，把原来全连接网络中的layer里的一些参数去掉就得到CNN。
8.1.1 Small Region
对于整张图来说，一些pattern是很小的。一个neural要指导一个图片里有没有一个pattern出现，并不需要取观察整张图片，而是只需要观察图片小部分即可。
所以，一个neural只需要连接到一个小块的区域就好，不需要连接到整张图。
所以，我们才可以用比较少的参数来做影像处理。
8.1.2 Same Patterns
相同的pattern会出现在图像的不同部分，但代表同样的含义。它们有同样的形状，可以用同样的neural，同样的参数就可以把patter侦测出来。
下图中，由于侦测鸟嘴的事情是相同的，所以可以共用一套参数，减少用到的参数的量。
8.1.3 Subsampling（下采样）
对像素进行下采样不会影响人对图片的理解。
例如：去除奇数行偶数列的像素之后，图片大小变成了之前的十分之一大小，不会影响人对这个图片的理解。
所以我们可以把图片变小，用更少的参数来处理图片。
8.2 ＣＮＮ－Convolution
前面的两个property可以用convolution来处理掉，最后的property可以用Max Pooling。
８.２.１ Ｐｒｏｐｅｔｒｙ １
每个filter中的值都是从训练数据中学出来的，而不是人为设计的。
每个filter如果是3* 3的detects，意味着它侦测一个3 *3的pattern(看3 *3的一个范围)。在侦测pattern的时候不看整张image，只看一个3 *3的范围内就可以决定有没有某一个pattern的出现。这个就是我们考虑的第一个Property。
将filter放在左上角，将image和filter做内积，并且不断按照stride步长移动，不断计算，直到移动到右下角。
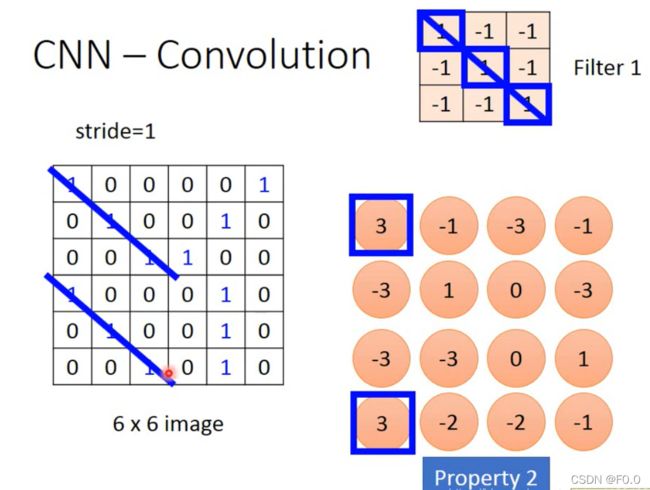
８.２.２ Ｐｒｏｐｅｔｒｙ ２
filter斜对角都是1，1，1，作用就是检测数据中有没有1，1，1。不论是左上角还是右下角，只要用一个filter即可检测出来，体现property2。
用另外一个filter得到蓝色的矩阵，红色和蓝色的矩阵结合起来，叫做feature map，有几个filter就会有多少个image。
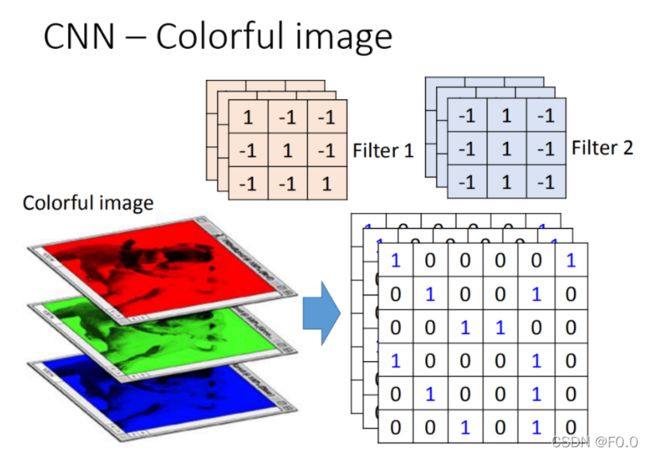
８.３ CNN－Ｃｏｌｏｒｆｕｌ Ｉｍａｇｅ
彩色图片，分成好几个矩阵叠加在一起，是一个立方体，处理彩色图片的filter也得是立方体。
卷积的值大意味着和patten相似。
８.４ Convolution v.s Fully Connected
Convolution 其实是Fully Connected layer拿掉一些weight 的结果
如图，一个neutral的weight只连接到1，2，3，7，8，9，13，14，15，其他的weight都没有。而这几个weight恰好就是filter里的参数。
在fully connect里面这两个neural本来是有自己的weight。当在做convolution时，首先把每一个neural连接的wight减少，强迫这两个neural共用一个weight，这件事就叫做shared weight。使得参数比原来的更少。
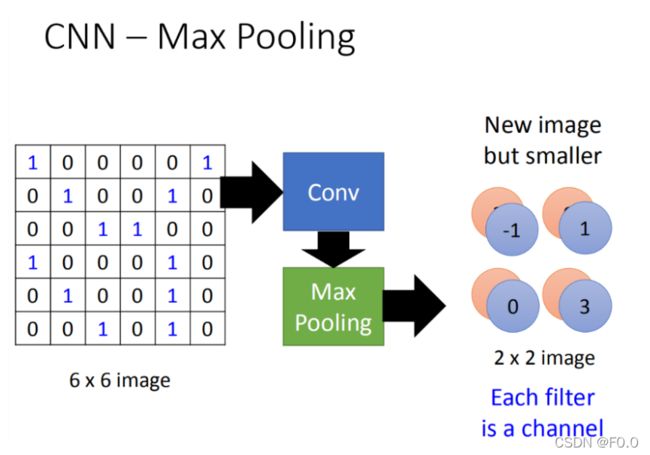
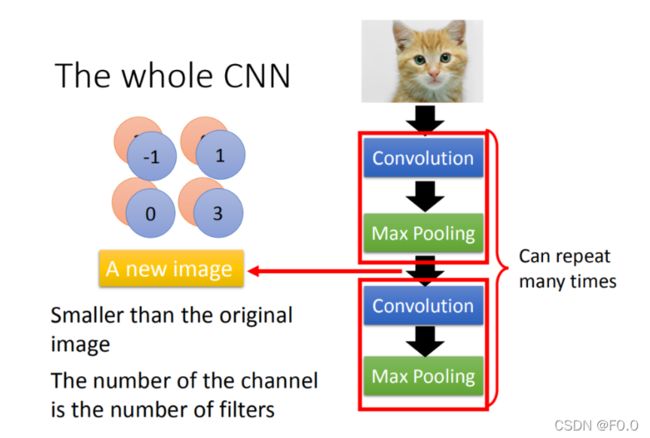
８.５CNN－Ｍａｘ Pooling
重复多次，可以得到一个新image，这个新的image比原来的小。
假设第一层filter有2个，在考虑第二层filter的ｉｎｐｕｔ时是会考虑深度的，并不是每个channel分开考虑，而是一次考虑所有的channel。所以convolution有多少个filter，output就有多少个filter(convolution有25个filter，output就有25个filter。只不过，这25个filter都是一个立方体)。
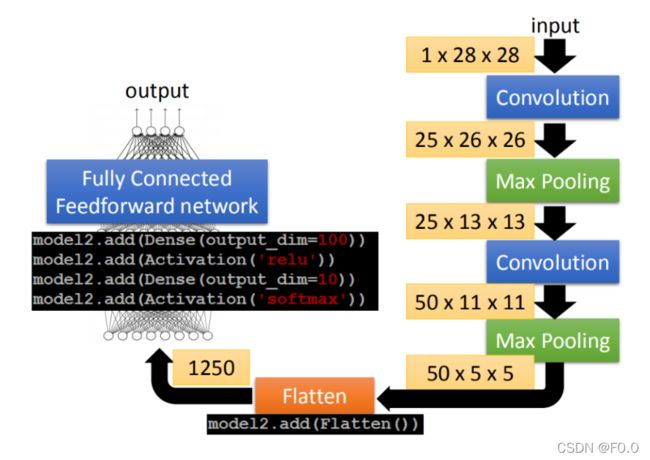
８.６ CNN－Ｆｌａｔｔｅｎ
flatten就是feature map拉直，拉直之后就可以丢到fully connected feedforward netwwork。
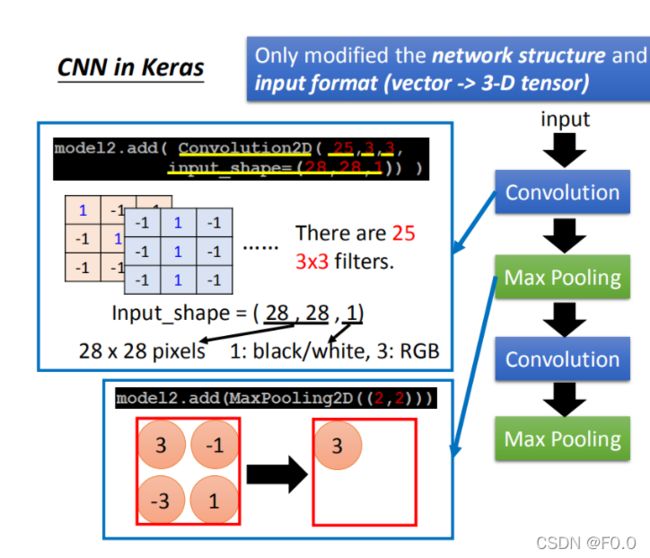
８.７ CNN ｉｎ Ｋｅｒａｓ
model.add(Convolution2D( 25, 3, 3)：25代表有25个filter，3 *3代表filter是一个3 *3的matrix
Input_shape=(28,28,1)：input是28 *28的image，每个pixel都是单一颜色。如果是黑白图为1(blacj/white)，如果是彩色的图时为3(每个pixel用三个值来表述)。
MaxPooling2D(( 2, 2 ))：2，2表示把2*2的feature map里面的pixel拿出来，选择max value
