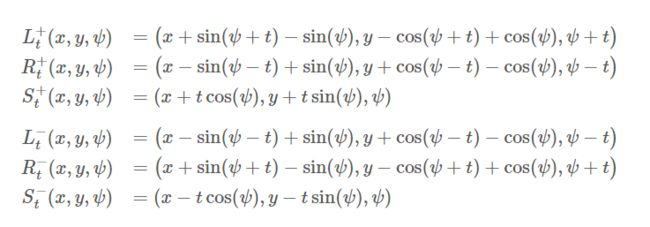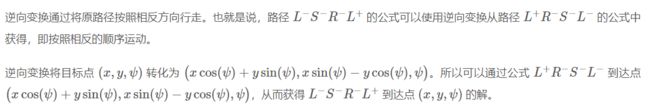Reeds-Shepp曲线学习笔记及相关思考
本篇博客主要记录在学习Reeds-Shepp曲线过程中的笔记及相关思考和概括总结
一、主要参考资料
1、提出Reeds-Shepp曲线的原始论文:【点击此处跳转】
2、路径规划 - ReedsShepp 曲线:【点击此处跳转】
3、Reeds-Shepp和Dubins曲线简介:【点击此处跳转】
4、自动驾驶-路径规划-ReedsShepp 曲线总结:【点击此处跳转】
5、【自动驾驶轨迹规划之dubins曲线与reeds-shepp曲线】:【点击此处跳转】
6、OMPL中给出的ReedsSheppStateSpace.cpp源码:【点击此处跳转】
7、Reeds-Shepp 曲线的Matlab实现:【点击此处跳转】
8、自动驾驶运动规划-Reeds Shepp曲线:【点击此处跳转】
9、HJ Sussman 和 G Tang的论文:【点击此处跳转】
二、Reeds-Shepp曲线简介
关于Dubins曲线的相关内容可查看我之前的笔记【点击此处跳转】
Reeds-Shepp曲线由 J.AReeds 和 L.A.Sheep 于 1990 年发表的论文 optimal path for a car that goes both forward and backwards中提出,是一种基于 Dubins 算法的改进算法, 详情见主要参考资料1。
相比于Dubins曲线只允许车辆向前运动,Reeds-Shepp曲线运动模型既允许车辆向前运动,也允许车辆向后运动。这就使得在某些情况下可以得出比 Dubins 曲线更优的解。如下图所示,其中左图为Dubins曲线,右图为Reeds-Shepp曲线
J Reeds和L Shepp证明Reeds Shepp Car从起点到终点的最短路径一定是下面的word的其中之一。word中的"|"表示车辆运动朝向由正向转为反向或者由反向转为正向,带π/2下标表示该段轨迹的弧长/弧长对应的角度为π/2。带β下标的相邻两段轨迹的弧长/弧长对应的角度相等,加号代表前行,减号代表倒车
展开后对应以下48种组合,尽管HJ Sussman 和 G Tang在70多页的论文中已经证明L-R+L-和R-L+R-这两种是多余的,依然还有46种组合, 详情见主要参考资料9。 相比于Dubins曲线只有6种可能的组合,Reeds-Shepp要复杂很多。
三、Reeds-Shepp曲线轨迹求解思路
1、位姿变化
在求解轨迹前,为方便运算,需要先对当前位姿和目标位姿进行变换,假设起始姿态为qi=(xi, yi,ψi),目标姿态为qg=(xg,yg, ψg),车辆转弯半径为r=ρ。首先将向量qiqg,平移到原点(0,0),平移量为(-x1,-y1)。则qi平移到(0,0),qg平移到(x2-x1,y2 -y1),然后再将向量qiqg旋转-ψ1度,(注意,是–ψ1度,很多参考资料里写的是ψ1度,是错误的),旋转后再将向量qiqg进行缩放,使其除以最小转弯半径ρ,这样就可以把最小转弯半径归一化为1,变换过程的公式如下所示:
2、六种基础运动公式
Reed-Shepp曲线允许进行倒车,因此车辆存在六种最基础的运动,即左转前进,右转前进ψ,直行前进,左转倒车,右转倒车,直行倒车,车辆从当前位姿(x,y,ψ)分别按照以上基础运动来运动弧长t(直行时代表直线距离)后对应的姿态如下所示:
(注:计算时会将最小转弯半径归一化为1,所以弧长t也对应转过的弧度制角度)
3、轨迹求解
假设经过位姿变化后的起点和目标点位姿分别为(0,0,0)和(x,y,ψ),假设要求解从起点到目标点的L+S+L+轨迹,则只需要将起点(0,0,0)代入到上面六种基础运动中的L+公式中,将结果再代入S+公式中,再将结果代入L+公式中,得到的结果与已知的目标点位姿(x,y,ψ)等价,因此可以得到3个等式,未知数便是基础运动公式中的t,代入了3次,即t1、t2、t3,或者可以用t、u、v来表示,如下面的公式所示:
同理,我们可以对其他的轨迹进行分析求解,上面举例的L+S+L+轨迹是较容易的一种,在求解其他轨迹时可能需要用到一些复杂的求解方法,我尚未找到完整的9种轨迹求解过程(为什么是9种,而不是48或46种将在下文中介绍), 主要参考资料2 中也仅仅给出了2种。(L+S+L+和L+S+R+)
4、类型变换
事实上,我们并不需要将48或者46种轨迹的求解公式都求出来,我们可以通过以下几种变换,以转换的形式以某种轨迹的求解公式来求其他轨迹的解,常见的变换有以下3种及其组合。
(1)时间变换 (timeflip)
时间变换通过交换轨迹字母上标符号+和- ,即车取反向的行进方向。举个例子, 从起点(0,0, 0)到目标点(x,y,ψ)的L-S-L-轨迹 可以通过从起点(0, 0,0)到点(-x,y,-ψ)的L+S+L+轨迹求得,因为两者关于x轴对称,如果感觉以上描述有些抽象,可以看一下 主要参考资料4 中给出的示意图。
再通俗一点讲,当我们需要求解 从起点(0,0, 0)到目标点(x,y,ψ)的L-S-L-轨迹 的时候,我们可以选择求解从起点(0, 0,0)到点(-x,y,-ψ)的L+S+L+轨迹,由于两个轨迹关于x轴对称,将得到的L+S+L+轨迹关于x轴对称变化后,即可得到我们真正想要求的轨迹,通过以上的转换,我们不再需要求解L-S-L-轨迹的求解公式,就可以得到L-S-L-轨迹。
(2)反射变换 (reflect)
反射变换通过交换轨迹字母中的R和L ,即将R变成L,将L变成R,举个例子, 从起点(0,0, 0)到目标点(x,y,ψ)的R+S+R+轨迹 可以通过从起点(0, 0,0)到点(x,-y,-ψ)的L+S+L+轨迹求得,因为两者关于y轴对称。
(3)逆向变换 (backwards)
5、类型变换的应用
通过反射变换,我们可以去掉表中所有R开头的轨迹(当然去掉L开头的轨迹也是可以的,为了与 主要参考资料6中给出的参考代码对应,我们以去掉R为例),直接去掉了24个,再通过时间变换,可以去掉剩下24个中L-开头的12种轨迹,只剩下了12种以L+开头的轨迹,如下图所示:
就拿c|c|c轨迹举例,去掉36种轨迹后,只剩下L+R-L+轨迹,利用时间变换可求被去掉的L-R+L-轨迹,通过反射变换可求被去掉的R+L-R+轨迹,通过时间+反射变换,可求被去掉的R-L+R-轨迹。
在剩下的12种轨迹中,通过时间变换+逆向变换,可以再次去掉轨迹L+R+L-和轨迹L+R-L-中的一种,这里以去掉L+R+L-为例,通过时间变换+反射变换+逆向变换,可以再次去掉轨迹8和9或去掉10和11,这里以去掉10和11为例,也就是说整个CSCC轨迹均被去掉了,这也解释了很多人疑问的程序中为什么没有CSCC轨迹代码,其实这并不是程序缺失,而是不需要有。现在就只剩下下图所示的9种轨迹了
也就是说,所有的48种轨迹均可以通过以上9种轨迹的求解公式,直接或间接的求解出来。
四、Reeds-Shepp曲线解是否一定存在
Reeds-Shepp曲线和Dubins曲线都是指没有障碍物时的最短路径。 主要参考资料3 中提到当存在障碍物时,只要存在连接起止位姿的无碰撞路径,那么就存在无碰撞的Reeds-Shepp曲线。然而这个结果对Dubins曲线却不适用。