基于matlab的球形译码的理论原理和仿真结果,对比2norm球形译码,无穷范数球形译码,ML检测
目录
1.算法描述
2.仿真效果预览
3.MATLAB部分代码预览
4.完整MATLAB程序
1.算法描述
多输入多输出(MIMO)系统通过使用考虑了时间和频率资源,多个用户,多个天线和其他资源的多个维度,可以增强通信系统的性能。在提高性能的同时,由于检测问题是NP-Complete,因此这些系统在检测方面提出了困难的计算挑战,并且对具有多项式复杂度的次优解决方案的需求也在不断增长。
机器学习领域的最新进展,特别是深度神经网络在解决几乎任何工程领域的许多问题方面的成功,表明使用机器学习进行数据驱动的检测方法可能会提供一种计算效率高的方法,以实现接近最佳的检测精度。
A. MIMO检测
MIMO检测是简单假设检验中的经典问题[1]。 最大似然(ML)检测器涉及穷举搜索,并且在最小误差联合误差的意义上是最佳检测器,用于同时检测所有符号。 不幸的是,它具有指数级的运行时复杂性,这使其在大型实时系统中不切实际。
为了克服最大似然解码器的计算成本,人们对实现次优检测算法非常感兴趣,该算法提供了更好,更灵活的精度与复杂度的权衡。在高精度条件下,球面解码算法[2] [3],[4]贝提出,基于晶格搜索,并提供了更好的计算复杂度,相对于完整搜索而言,其准确性会降低。 在另一种情况下,最常见的次优检测器是线性接收器,即匹配滤波器(MF),解相关器或迫零检测器(ZF)和最小均方误差(MMSE)检测器。 更高级的检测器基于决策反馈均衡(DFE),近似消息传递(AMP)[5]和半确定松弛(SDR)[6],[7]。当前,在许多实际情况下,AMP和SDR均可提供接近最佳的精度。AMP在实践中实现起来简单且便宜,但是它是一种迭代方法,可能会在挑战性环境中产生差异。SDR更加健壮,具有多项式复杂性,但是它所解决的设置受到限制,并且在实践中要慢得多
球形译码的基本思想是在以一个矢量x 为中心的半径为d的多维球内搜索格点,通过限制或者减少搜索半径从而减少搜索的点数,进而使得计算时间减少。球形译码算法带来的优点在于它不需要象传统的最大似然译码算法那样需要在整个格内对所有的格点进行搜索,而只需要在一个事先设定的有限球形区域进行搜索,如果该区域所包含的点数相对于整个格内的总点数是相当小的,搜索时间就会大大减少。
影响球形译码的关键问题有:(1) 怎样选择搜索半径d。如果d太大,则球内会包含太多的点,复杂度就会接近或者达到最大似然译码的指数级复杂度。如果d 太小,则球内可能一个格点都不包含,那么球形译码算法将得不到合理的解。(2) 怎样才能判断一个点是否在球内。如果这种判断需要借助每一个格点和矢量之间的距离来判断的话,那么这种方法就不太理想,因为我们需要考察所有的点,所产生的计算量也是指数级的。
球形译码解决了第2个问题,此处均考虑信号为实数,因为复数可以通过增加一倍的维数,将实部和虚部分开,要判断一个点是否在半径为d的m维球内比较困难。若将m变为1,则从球退化为一个间距,这个点就相当于某根天线发送信号的实部或虚部,这样操作就简单很多,可以知道这个点是否在这个距离内。多根发送天线上的信号的实部和虚部分成很多维,每一维上有可能取值。球形译码算法相当于构建了一棵树,树的第k层节点对应的是落在半径为d,维数为k的球内的格点。
如果要求性能完全符合最大似然检测的性能,则初始半径必须是一系列的值,选定初始值为d,如果在范围为d时寻找不到合适的点,则需要增大d的值,扩大的倍数为2倍;如果要求性能接近于最大似然检测的性能,则初始半径相比上面,要取较大,必须有一定的冗余。
对于只要求性能接近最大似然检测的性能的二范数的球形译码,初始半径的选取有公式如下:
对于性能要求达到最大似然检测的性能的二范数的球形译码,初始半径的的选取有公式如下:
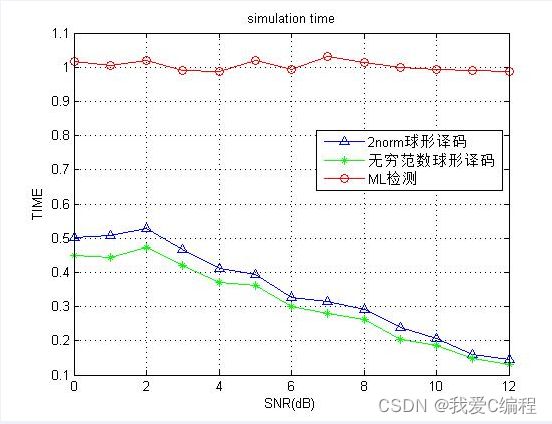
2.仿真效果预览
matlab2022A仿真结果如下:
3.MATLAB部分代码预览
msg=randint(log2(mod_num),Nt*Number/2);
h=modem.qammod('M',mod_num,'InputType','bit','symbolorder','Gray');%qam调制
s=modulate(h,msg);
constelPoints=[1+j 1-j -1+j -1-j]; %$ for ML detect
% constelPoints=[-3-3*j -3-j -3+3*j -3+j -1-3*j -1-j -1+3*j -1+j 3-3*j 3-j 3+3*j 3+j 1-3*j 1-j 1+3*j 1+j];
s1=[real(s);imag(s)]; %s1为信号的实矩阵
s2=reshape(s,Nt,Number/2); %s2为信号的Nt行的复矩阵
if mod_num==4
codebook=[-1 1]; %表示在变为实矩阵后,4qam只有两种情况1和-1
end
if mod_num==16 %表示在变为实矩阵后,16qam有4种情况
codebook=[-3 -1 1 3];
end
ss=reshape(s1,2*Nt,Number/2); %ss为信号的2*Nt行的实矩阵
% H=[real(H1(:,:,round)) -imag(H1(:,:,round));imag(H1(:,:,round)) real(H1(:,:,round))]; %将信道复矩阵变为信道实矩阵
%/%
r1=H1(:,:,round)*s2;
for ii=1:Nt %添加噪声
rr(ii,:)=awgn(r1(ii,:),snr_1(ISNR),'measured');
end %rr为接收复信号
C1=3*(2*Nt)*2*(2/(10^(snr(ISNR)/10))); %初始半径 二范数4qam
C2=16*2*(2/(10^(snr(ISNR)/10))); %初始半径无穷范数
rev1=[real(rr);imag(rr)]; %rr转变为实信号
H=[real(H1(:,:,round)) -imag(H1(:,:,round));imag(H1(:,:,round)) real(H1(:,:,round))]; %信道实矩阵
for tmp=1:Number/2 %二范数球形译码
rev=rev1(:,tmp);
tic
y_2norm_temp = spheredecode(rev, C1, H, codebook);
for jj=1:Nt
y_2norm(Nt*tmp+jj-Nt)=y_2norm_temp(jj)+j*y_2norm_temp(jj+Nt); %存储为复数形式
end
t1(ISNR)=toc+t1(ISNR);
end
H=[real(H1(:,:,round)) -imag(H1(:,:,round));imag(H1(:,:,round)) real(H1(:,:,round))]; %信道实矩阵
for tmp=1:Number/2 %二范数球形译码
rev=rev1(:,tmp);
tic
y_infnorm_temp = spheredecodeinf(rev, C2, H, codebook);
for jj=1:Nt
y_infnorm(Nt*tmp+jj-Nt)= y_infnorm_temp(jj)+j* y_infnorm_temp(jj+Nt); %存储为复数形式
end
t2(ISNR)=toc+t2(ISNR);
end
for tmp=1:Number/2
min=100000;
tic
for flag1=1:mod_num
for flag2=1:mod_num
for flag3=1:mod_num
for flag4=1:mod_num
stmp=[constelPoints(flag1);constelPoints(flag2);constelPoints(flag3);constelPoints(flag4)];
rtmp=rr(:,tmp);
Maximum=norm(rtmp-H1(:,:,round)*stmp);
if Maximum4.完整MATLAB程序
matlab源码说明_我爱C编程的博客-CSDN博客
V