IoU系列损失详解
IoU相关损失详解
IoU 计算公式及原理解析
IoU的全称为交并比(Intersection over Union),即表示为“预测边框(bounding box )”和“真实边框(ground truth)“的交集和并集的比值。即IoU的计算公式为:
I o U = ( A ∩ B ) A ∪ B IoU =\frac{(A \cap B)} {A \cup B} IoU=A∪B(A∩B)
用图像可以更直观的表示,其表示如下:

即IoU相当于两个区域交叉的部分除以两个区域的并集部分得出的结果。
当系统在训练模型的过程中,通常使用bounding box 与ground truth 之间的IoU值大小来判断该结果是不是一个好的结果;一般情况下,认为IoU > 0.5就算是一个不错的预测结果。
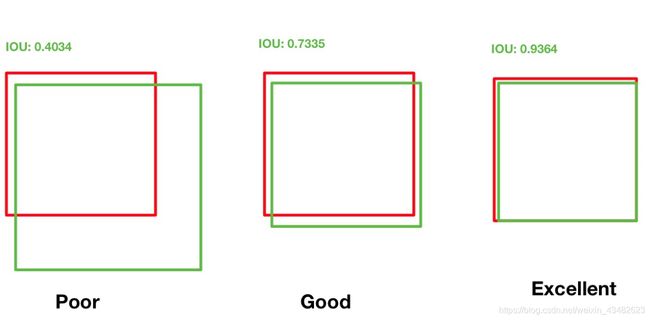
如上图所示,其中Poor所表示的是bounding box 与ground truth的IoU值为0.4034,即IOU < 0.5,所以就认为该预测结果较差,并不是系统所需要的结果(预测不准确)。
Good所表示的是bounding box 与ground truth的IoU值为0.7335,即IOU > 0.5,所以就认为该预测结果较好,且满足系统的一般需要(可将其判断预测准确)。
Excellent所表示的是bounding box 与ground truth的IoU值为0.9364,即IOU > 0.5,所以就认为该预测结果较好,满足系统的一般需要,且说明预测相当准确。
当然,该阈值的大小可根据训练的模型自行改变,但通常情况下使用0.5。
IoU Loss
IoU Loss 的提出

如上图所示,可知道 L2 loss以及 IoU loss的基本计算方式,暂时先不介绍其计算方式,先看下图。
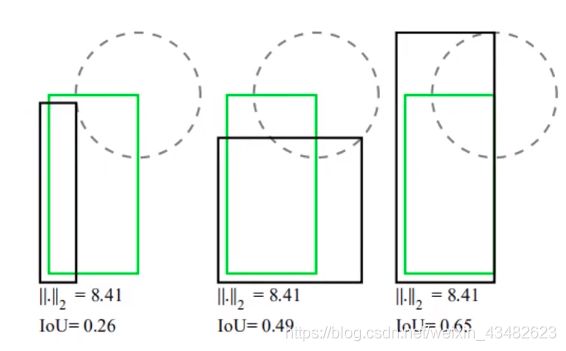
在上诉图像中,可以看出图中所有目标的L2 Loss都一样,但是第二个的IoU显然是要大于第一个,第三个的IoU显然是要大于第二个,由图像分析可知,第三个矩形框的检测结果相对来说是最好的。
当所有目标的L2 Loss是一样,但IoU却存在差异。通过4个点回归坐标框的方式是假设4个坐标点是相互独立的,没有考虑其相关性,实际4个坐标点具有一定的相关性。因此引入了IoU Loss。
IoU Loss计算方式
IoU计算公式一:
I o U L o s s = − ln ( I o U ) = − ln ( ( A ∩ B ) A ∪ B ) IoU Loss = - \ln(IoU) = - \ln(\frac{(A \cap B)} {A \cup B}) IoULoss=−ln(IoU)=−ln(A∪B(A∩B))
IoU计算公式二:
I o U L o s s = 1 − I o U = 1 − ( A ∩ B ) A ∪ B IoU Loss = 1 - IoU = 1 - \frac{(A \cap B)} {A \cup B} IoULoss=1−IoU=1−A∪B(A∩B)
其中公式二在使用过程中比较常见。
IoU Loss的优缺点
优点:
1、能够更好的反映重合程度
2、具有尺度不变性
缺点:
1、当bounding box 与 ground truth 不相交时,IoU为0,即在此情况下,将无法计算IoU Loss,因而导致其梯度为0并且无法进行优化。因而引入了GIoU Loss。
GIoU Loss(Generalized IoU)
GIoU Loss 定义

上图中绿色的边界框代表:真实的边界框(ground truth);红色的边界框代表:预测的边界框(bounding box);而蓝色的边界框代表:使用最小的矩形框将ground truth和bounding box框住,此处使用C表示。
则GIoU的公式为:
G I o U = I o U − C − ( A ∪ B ) C GIoU = IoU - \frac{C - (A \cup B)} {C} GIoU=IoU−CC−(A∪B)
由公式计算可知,其GIoU的取值范围为:
− 1 ≤ G I o U ≤ 1 -1 \leq GIoU \leq 1 −1≤GIoU≤1
当ground truth 和 bounding box 完美重合在一起的时候,则三者的面积相等,那么就有:
C − ( A ∪ B ) C = 0 \frac{C - (A \cup B)} {C} = 0 CC−(A∪B)=0
因而在此情况下 GIoU = IoU = 1。
而当ground truth 和 bounding box 不相交且两边界框相距无穷远时,则有:
C − ( A ∪ B ) C ≈ 1 \frac{C - (A \cup B)} {C} \thickapprox 1 CC−(A∪B)≈1
所以由GIoU = IoU - 1,且此时IoU = 0,即GIoU = -1。由此可得出GIoU的取值范围。
而GIoU Loss 的计算公式为:
G I o U L o s s = 1 − G I o U GIoU Loss = 1 - GIoU GIoULoss=1−GIoU
由公式计算可知,其GIoU的取值范围为:
0 ≤ G I o U L o s s ≤ 2 0 \leq GIoU Loss \leq 2 0≤GIoULoss≤2
GIoU Loss 缺点

当ground truth 和 bounding box 等宽高且处于同一水平或同一垂直线时,可知:
C − ( A ∪ B ) C = 0 \frac{C - (A \cup B)} {C} = 0 CC−(A∪B)=0
那么GIoU = IoU ,即GIoU退化为IoU。
DIoU Loss
DIoU Loss 定义
由于IoU Loss 和 DIoU Loss 存在两个问题,其一是收敛较慢(Slow Convergence);其二是回归不精确(Inaccurate Regression)。因而提出了DIoU Loss(Distence-IoU).
DIoU计算公式:

其中DIoU的取值范围为(计算方式与GIoU及计算方式相同):
− 1 ≤ D I o U ≤ 1 -1 \leq DIoU \leq 1 −1≤DIoU≤1
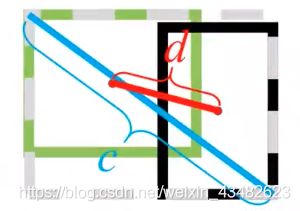
那么公式中的d 和 c 分别表示什么,如下图所示:
绿色边界框:实际边界框,即ground truth;
灰色边界框:即使用最小的矩形框将ground truth和bounding box框住的矩形框。
b:预测框的中心坐标;
b^gt:实际框的中心坐标;
d:两边界框中心点之间的欧式距离;
c:最小矩形框两对角顶点之间的欧式距离。
即DIoU Loss计算公式如下:
D I o U L o s s = 1 − D I o U DIoU Loss = 1 - DIoU DIoULoss=1−DIoU
由公式计算可知,其DIoU的取值范围为:
0 ≤ D I o U L o s s ≤ 2 0 \leq DIoU Loss \leq 2 0≤DIoULoss≤2
DIoU Loss 分析

上图中第一行使用的是GIoU损失进行网络训练,不难分析出,当其迭代到400次时,其bounding box才勉强与ground truth重合到一个较好的效果;而第二行使用的是DIoU损失训练网络,当迭代40次时,便与ground truth有重合部分;而当迭代120次时,bounding box与ground truth便已经完全重合。即使用DIoU Loss收敛速度明显快于GIoU Loss的收敛速度。

上图中同样的给出了三组预测边界框和实际边界框的重合关系,不难得出,在这三组重合关系中,其重合的位置是不同的,但是其IoU Loss与GIoU Loss是相同的,都为0.75;即说明这两种损失无法表示出bounding box与ground truth的重合关系。而DIoU Loss是不同的,其分别为0.81、0.77、0.75。
因为DIoU Loss能够直接最小化两个boxes之间的距离,因此其收敛速度比IoU Loss与GIoU Loss更快
CIoU Loss
CIoU Loss定义
一个优秀的回归定位损失应该考虑到3种几何参数:重叠面积、中心点距离、长宽比;
由此提出了CIoU Loss。
CIoU的计算公式如下:
b^gt:实际框的中心坐标;
d:两边界框中心点之间的欧式距离;
c:最小矩形框两对角顶点之间的欧式距离。
w^gt:(真实框)ground truth的宽;
h^gt:(真实框)ground truth的高;
w:(预测框)bounding box的宽;
h:(预测框)bounding box的高。
即CIoU Loss计算公式如下:
C I o U L o s s = 1 − C I o U CIoU Loss = 1 - CIoU CIoULoss=1−CIoU
各类损失实际效果对比

上述表格不难看出,由IoU损失到CIoU损失,其效果是逐渐增强的,即识别准确率逐步增加。