WGCNA总结笔记：深入研究算法及其实现原理（1）

一、前言

WGCNA全称为Weighted gene co-expression network analysis（也有叫weighted
correlation network analysis）即加权基因共表达网络分析。目的是用数学、计算机科学的思想和方法挖掘样品的基因表达量数据与其表型数据里具有生物学意义的结论。本文研究的是R语言WGCNA包的算法、计算、实现过程等，其中涉及到了关于图论、线性代数等数学知识，由于本人正在准备考取数学系研究生，因此以WGCNA为例子展开研究，也借此拓展这一领域的知识。由于我也是在学习阶段，且英语水平不高，阅读英文文献及英文书籍容易有理解错误，希望能以此文抛砖引玉，如有遗漏或错误请批评指正~
由于时间关系，对于聚类分析的数学思想和算法实现暂未研究，因此聚类分析的步骤略过，以后在假期再深入学习研究。

二、WGCNA分析流程

WGCNA根据需要计算的步骤可大致分成以下几个步骤：
1.数据前处理
2.构建加权相关性邻接矩阵
3.计算拓扑重叠矩阵
4.对基因进行层次聚类，划分模块

目前只研究了1、2、3中的一些算法实现，将来继续研究时再写一篇文进行补充。

三、数据前处理

首先，WGCNA需要的目标数据是储存有若干样本以及其对应的各基因表达量的数据集，经过数据前处理将其转化为合适的数据结构，以进行后续的分析。

格式处理

我们需要的样本为由m个样本、n个基因构成的m x n矩阵，矩阵内的元为某样本中某基因的基因表达量值。获取数据后先检查其数据是否符合格式，例如如果样本和基因行列对调了，将其矩阵转置即可。

样本聚类分析排除异常值（可选）

如果不确定样本数据是否可靠，例如是否有异常值，可以对样本数据进行一次聚类分析，若有某样本有异常值，则其在聚类分析后可视化显离群现象，可考虑将其剔除。

四、构建加权相关性邻接矩阵

计算基因表达量的相关系数

对于数据前处理构成的m x n矩阵，取每两两基因在所有样本中的表达量（即取任意两列），得两个列向量。由于基因表达量数据参差不齐，有时偏差较大，因此对列向量进行以下方法的标准化，以便后续的计算：

其中Xu为原向量，scale（X）u为标准化后的向量。其中，mean函数与var函数定义如下：


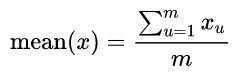
对两个标准化后的列向量以pearson相关（ Pearson correlation）进行线性相关水平计算。

可以看出这是线性代数中向量内积的计算方法，根据向量的夹角余弦值判断向量的线性相关性。区别在于在WGCNA方法中根据数据（基因表达量）本身的特点对向量进行了标准化。

（在R语言的WGCNA包中，涉及到线性相关系数计算均采用Pearson相关系数法，后文将不再赘述）

得到n x n的半对称矩阵S，其中Sij即为基因i与基因j的相关系数。

对相关系数邻接矩阵加权优化（软阈值法）

在说之前，先介绍两个概念：随机网络和无标度网络。在数学的图论中，这里提到的网络其实就是图的概念。

随机网络的概念是：在网络中所有点之间的关联性都差不多，可以看做是随机连接而形成的。

无标度网络的概念是：在网络中有极少数的中心点与网络里大部分的点连接，而大部分的点只与那些极少数的中心点连接。

再介绍一个度的概念：度可以理解为网络中某个结点相连的线段数量。

事实上，无标度网络更符合我们认知的事实：极少数的基因执行着生物体中更多的功能，而大多数的外围基因执行着较少的，较为边缘的功能。在受到外因伤害时，无标度网络下的基因会有更强的抵抗力，只要中心基因不受影响，伤害可以忽略不计；而随机网络下的基因在受到外因伤害时，其受损程度和伤害程度完全成正比。因此这也是符合生物进化论中适者生存的理论的。

无标度网络的定义是：假设在网络中任取一个结点，取到一个度数为d的结点的概率为P(d)，且P(d)与d的概率分布满足幂律分布：

由于d和p(d)取值范围均为0到正无穷，因此可以取对数变换得：

可以看出，如果网络完全符合无标度网络的特征，则其概率密度函数取对数后的logP(d)与logd线性相关。基于这个原理，我们对各个结点的度数d及该度数在所有结点度数中的占比进行pearson线性相关分析，得到关于无标度网络的适应系数（scale-free fitting index R2）。这个系数可以评定构建的网络接近无标度网络的程度，越接近1则越像无标度网络，越接近0则越像随机网络。

基于以上理论，就产生了给基因的相关系数加上一个指数β的想法。当β＞1时，不同的相关系数之间的差距会越来越大。例如基因A和基因C的相关系数为0.3，基因A和B为0.6，当给他们加上β=2的次方时，相关系数变为0.09和0.36，放大了其相关系数差异的显著程度。这个β可以根据前文提到的无标度网络适应系数进行选择，例如我们要构建无标度网络适应系数大于0.9的网络，就计算各个β值加权后网络的无标度网络适应系数，超过0.9的最小β是最优选择。

在R语言的WGCNA包中pickSoftThreshold函数已将此功能实现并可视化，可供手动选择β的值。

确定了加权的权重β后对原有的相关系数矩阵加权，得到加权基因相关性矩阵A：

至此，加权的基因相关性矩阵构建完毕。

五、计算拓扑重叠矩阵

如果直接以上一步得到的两两基因间的加权相关系数进行模块识别和划分准确性较差，且对数据的利用度也不高。因此引入拓扑重叠矩阵的概念。

这个概念可以通过一个社交网络的例子解释：假设A、B同属于同一个公司，且A与B不认识，互相无关联，但A与B都各有该公司的很多共同好友，则可以认为A与B的社交网络重叠性强，因此认为A与B在同一模块（所属的公司）。

在WGCNA中应用类似：如果基因i和基因j之间可以通过若干个中间关联的基因u而形成联系，则这个联系的强弱也会一定程度上被考虑进划分模块的依据中。在WGCNA中，拓扑重叠矩阵的计算方法为：

个人认为这一步是WGCNA分析的精髓所在。以u为遍历子，遍历基因列表里除i，j以外的所有基因，并将u与i，j之间的相关系数以上式运算，巧妙地用其他基因作为桥梁将i，j基因在网络中的表现的重叠程度数据化。若i，j在网络中连接情况越相似，则TOMij越大，i和j越有可能在同一表达模块中。

至此，拓扑重叠矩阵计算完毕。

结束语

第一部分就暂时写到这里。对于后续的层次聚类划分模块的算法，先挖个坑以后有时间再更新。最后的目标是做一个python的库实现wgcna的分析，如果有好的提议希望指出，此外文章中如有错误希望大家不吝赐教，感谢~

参考书目

Steve Horvath . Weighted Network Analysis Applications in Genomics and Systems Biology . Springer New York Dordrecht Heidelberg London . ISBN 978-1-4419-8818-8