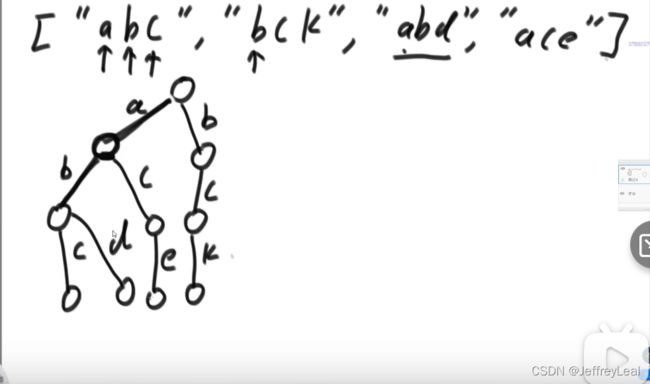一周刷爆LeetCode,算法da神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解 笔记
一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解 笔记
- 教程与代码地址
- P1 出圈了!讲课之外我们来聊聊算法和数据结构!以及未来!
- P2 1.认识复杂度和简单排序算法
-
- 基础第一课题目二:选择排序、冒泡排序
-
- 选择排序
- 冒泡排序
- 基础第一课题目五:异或运算
-
- 例题
- 基础第一课题目三:插入排序
- 基础第一课题目四:二分法的详解与扩展
- 基础第一课题目六:对数器的概念和使用
- P3 2.认识O(NlogN)的排序
-
- 基础第一课题目七:递归排序
- 基础第二课题目一:归并排序
- 基础第二课题目二:归并排序的扩展
-
- 小和问题
- 逆序对问题
- 基础第二课题目六:荷兰国旗问题
- 基础第二课题目七:快速排序
- P4 3.详解桶排序以及排序内容大总结
-
- 基础第二课题目五:堆排序扩展题目
- 基础第三课题目二:桶排序
- P5 4.链表
-
- 基础第三课题目三:排序算法的稳定性及其汇总
- 基础第四课题目一:哈希表的简单介绍
- 基础第四课题目二:有序表的简单介绍
- 基础第四课题目九:按某值划分单向链表
- 基础第四课题目十:复制含有随机指针节点的链表
- P6 5.二叉树
-
- 基础第四课题目十一:两个单链表相交
- 基础第五课题目一:二叉树节点结构
- P7 6. 图
-
- 基础第五课题目二:二叉树的相关概念及其实现判断
-
- 判断是否搜索二叉树
- 判断是否完全二叉树
- 判断是否是满二叉树
- 判断是否是平衡二叉树
- 树形DP
- 基础第五课题目三:二叉树的公共祖先
- 基础第五课题目四:二叉树的后继节点
- 基础第五课题目五:二叉树的序列化和反序列化
- 基础第五课题目六:折纸问题
- P8 7.详解前缀树和贪心算法
-
- 基础第六课题目一:图的存储方式
- 基础第六课题目二:优先遍历
-
- 图的宽度优先遍历
- 广度优先遍历
- 基础第六课题目三:拓扑排序
- 基础第六课题目四:kruskal算法
- 基础第六课题目五:prim算法
- 基础第六课题目六:Dijkstra算法
- P9 8. 暴力递归
-
- 基础第七课题目一:前缀树
- 基础第七课题目二:贪心算法
- 基础第七课题目七:会议室宣讲安排
- 基础第七课题目三:贪心算法解题套路
- 基础第七课题目四:字符串拼接题目证明
- 基础第七课题目六:金条分割
- 基础第七课题目八:银行家问题
- 基础第七课题目九:找中位数
- 基础第八课题目九:N皇后问题
- P10 9. 补充视频
-
- 基础第六课题目六:Dijkstra算法补充
- 基础第八课题目二:汉诺塔问题
- 基础第八课题目三:打印子集
- 基础第八课题目四:打印字符串全部排列
- 基础第八课题目八:2玩家左右抽牌
- 基础第八课题目五:逆序栈
- 基础第八课题目六:数组转字符
- 基础第八课题目七:装载最大价值
- P11 10.基础提升 哈希函数与哈希表等
- P12 11.基础提升 有序表、并查集等
- P13 12.基础提升 KMP、Manacher算法等
- P14 13.基础提升 滑动窗口、单调栈结构等
- P15 14.基础提升 二叉树的Morris遍历等
- P16 15.基础提升 大数据题目等
- P17 16.基础提升 暴力递归(上)等
- P18 17.基础提升 暴力递归(下)等
- P19 18.中级提升班-1
- P20 19.中级提升班-2
- P21 20.中级提升班-3
- P22 21.中级提升班-4
- P23 22.中级提升班-5
- P24 23.中级提升班-6
- P25 24.中级提升班-7
- P26 25.中级提升班-8
- P27 26.中级提升班-9
- P28 27.中级提升班-10
- P29 28.高级进阶班-1
- P30 29.高级进阶班-2
- P31 30.高级进阶班-3
- P32 31.高级进阶班-4
- P33 32.高级进阶班-5
- P34 33.高级进阶班-6
- P35 34.高级进阶班-7
- P36 35.高级进阶班-8
- P37 36.高级进阶班-9
- P38 37.高级进阶班-10
- P39 38.高级进阶班-11
教程与代码地址
笔记中,图片和代码基本源自up主的视频和代码
视频地址:一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解
代码地址:
讲义地址:
如果想要爬虫视频网站一样的csdn目录,可以去这里下载代码:https://github.com/JeffreyLeal/MyUtils/tree/%E7%88%AC%E8%99%AB%E5%B7%A5%E5%85%B71
P1 出圈了!讲课之外我们来聊聊算法和数据结构!以及未来!
P2 1.认识复杂度和简单排序算法
数组在内存空间中,是连续的区域;
列表在内存中不是连续的,而是一个指针指向下一个指针。
常数时间的操作:一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。比如数组的寻址操作,得到arr[i]的值,只需要起始地址+i就能算到该位置的地址,得到该位置上得值,是常数操作。而列表的寻址,就要逐个遍历,才得到list[i],这就不是常数操作。
基础第一课题目二:选择排序、冒泡排序
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零:

先找最小,次小,次次小…如此类推,一共n轮排序,每轮排序记录次轮比较中最小元素的位置,然后交换。
复杂度,在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,常数操作复杂度为 O ( N 2 ) O(N^2) O(N2):

看:看了多少眼;
比:2数比较,比较应该比看要少一次;
swap:交换,比较的过程只记录第i轮排序和第j个位置的下标,所以每一轮只交换了一次。
代码:
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。 它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。

两两比较,大的右移,比较窗口滑动,直到最大的数放到最后,结束一轮比较,再开始下一轮。
此算法时间复杂度也为 O ( N 2 ) O(N^2) O(N2)。
基础第一课题目五:异或运算
异或运算,异或操作性质:一个数与自身异或=自身

位运算,先转换为2进制表示,运算完后,再转回10进制:
public class Test {
public static void main(String[] args) {
int a = 7;
int b = 4;
int c = a^b;
int d = a^b^a;
System.out.println(c);
System.out.println(d);
}
}
控制台:
3
4
Process finished with exit code 0
下面三行代码跑完,2个数完成互换:

这么做的前提2个交换数的内存地址不能一样,不然就是自身与自身异或,结果是0。
例题
1)数组中,一个数出现了奇数次,其他数出现了偶数次,要找奇数次的数
答案:将所有数都异或,最后只剩下奇数次的数。
public static void printOddTimesNum1(int[] arr) {
int eO = 0;
for (int cur : arr) {
eO ^= cur;
}
System.out.println(eO);
}
1)数组中,2个数a,b出现了奇数次,其他数出现了偶数次,要找奇数次的数
答案:将所有数都异或,得到eor=a异或b;因为a!=b,所以eor!=0,必造成eor有一个位上为1,那个位就能用来区分a和b。
eor & (~eor + 1);//选出e0最右边的一个1:

public static void printOddTimesNum2(int[] arr) {
int eO = 0, eOhasOne = 0;
for (int curNum : arr) {
eO ^= curNum;
}
int rightOne = eO & (~eO + 1);//选出e0最右边的一个1,
for (int cur : arr) {
if ((cur & rightOne) != 0) {
eOhasOne ^= cur;//最后得到的这个数,是这一个位上有1的数,与其他数的异或
}
}
System.out.println(eOhasOne + " " + (eO ^ eOhasOne));
}
基础第一课题目三:插入排序
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
算法步骤:
0~1范围有序;
0~2范围有序,将第二个位置的数插入到前面,排好序就停下,所以比较的次数与数据的结构有关。
算法复杂度,只计算最坏情况的复杂度。此算法时间复杂度也为 O ( N 2 ) O(N^2) O(N2)。
![]()
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
//判断条件,j >= 0:换到最后就停,arr[j] > arr[j + 1]排好序就停
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
基础第一课题目四:二分法的详解与扩展
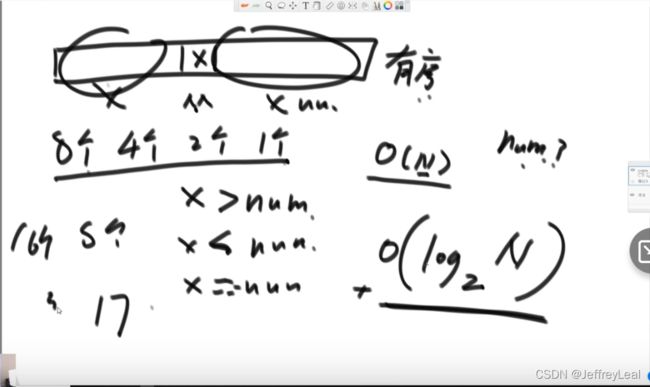
2)在一个有序数组中,找>=某个数最左侧的位置
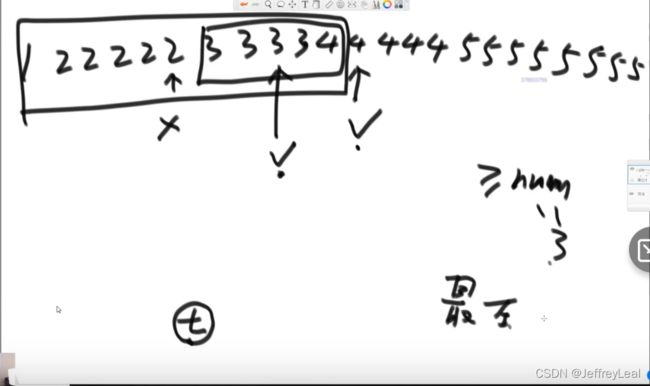
2分找到数,还要继续,直到最左侧停止。
3)局部最小值问题,数组无序,任何两个相邻的数不相等,局部最小值定义为既小于左边数,也小于右边数。
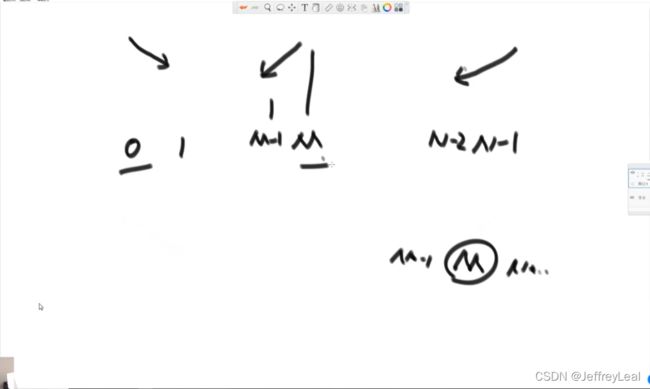
用的是零点定理的思想,上图中,3个位置的趋势,左边两个趋势,中间必有最小值。
基础第一课题目六:对数器的概念和使用
算法c是自己写的,算法b是系统提供的排序算法,使用随机数组,2种算法对比,看c是否有错。不依赖线上测试平台,自己就能测出来。
对数器:
public static void comparator(int[] arr) {
Arrays.sort(arr);
}
P3 2.认识O(NlogN)的排序
基础第一课题目七:递归排序
用递归方法找一个数组中的最大值,系统上到底是怎么做的?
求中点,第一行L+R可能会溢出,第三行使用右移一位就是除以2。
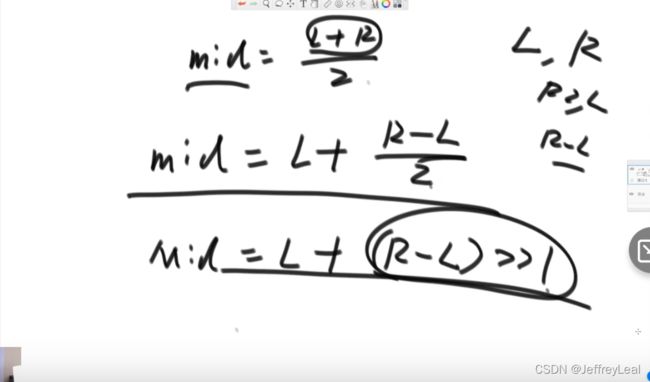
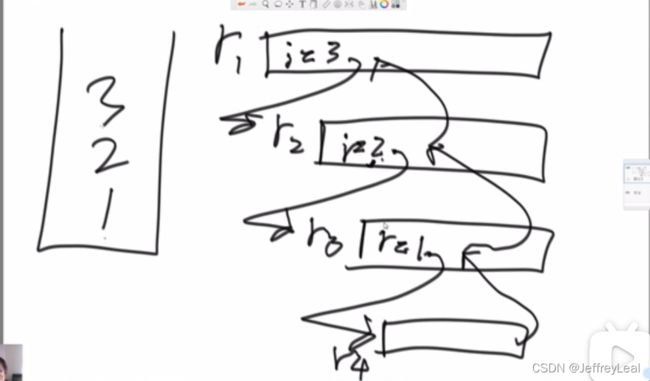
递归函数的拆分:

由上往下,不断进栈,多叉树,每一条叉都会进栈出栈,实现遍历。
public static int getMax(int[] arr) {
return process(arr, 0, arr.length - 1);
}
public static int process(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
int mid = L + ((R - L) >> 1);
int leftMax = process(arr, L, mid);
int rightMax = process(arr, mid + 1, R);
return Math.max(leftMax, rightMax);
}

使用此公式的前提是子问题的规模要一致。

左边是母问题的复杂度,右边第一项是子问题的复杂度,第二项为其余操作的复杂度。
上述代码,2个子问题的规模都是N/2,加上一次if,一次算中点,一次比较,这3个常数操作的总复杂度是 O ( 1 ) O(1) O(1)。
基础第二课题目一:归并排序
归并排序的主要思想是分治法。主要过程是: 将n个元素从中间切开,分成两部分。(左边可能比右边多1个数) 将步骤1分成的两部分,再分别进行递归分解。直到所有部分的元素个数都为1。 从最底层开始逐步合并两个排好序的数列


public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {//一直往help里面黏贴,同时p1或p2指针一直右移直至越界
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p1++];
}
while (p2 <= r) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {//把排好序的help数组黏贴到原始数组的位置
arr[l + i] = help[i];
}

子问题mergeSort的规模都是N/2,merge的复杂度是N,母问题的复杂度为 O ( N ∗ log N ) + O ( N ) O(N*\log N)+O(N) O(N∗logN)+O(N)。选择排序,冒泡排序,插入排序,都是有大量重复的比较,浪费了比较的信息,而归并排序,用空间换了时间,每次比较都没有被浪费,每次比较都进行排序,所以复杂度低。

基础第二课题目二:归并排序的扩展
小和问题

直接遍历的复杂度:
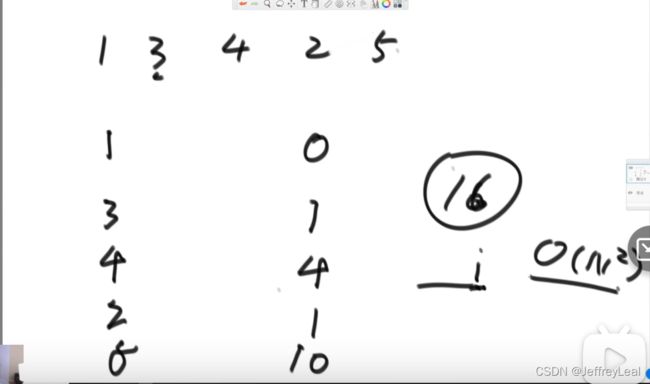
问题可以转换为,算一个数,右边有多少个数比他大:比1大有4个,比3大有2个…

其实就是在递归合并里面加了一行代码,计算右边数组中,有多少个数比p1指针所指的数要大。
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return mergeSort(arr, 0, arr.length - 1);
}
public static int mergeSort(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return mergeSort(arr, l, mid) //左侧排序求小和
+ mergeSort(arr, mid + 1, r) //右侧侧排序求小和
+ merge(arr, l, mid, r);//2侧排序求小和
}
public static int merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;//记录右边的数组有几个数比左边当前数要大
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];//一直往help里面黏贴,同时p1或p2指针一直右移直至越界,将2个数组合并重排
}
while (p1 <= m) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p1++];
}
while (p2 <= r) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {//把排好序的help数组黏贴到原始数组的位置
arr[l + i] = help[i];
}
return res;
}
逆序对问题
在一个数组中,左边的数如果比右边的数大,则折两个数构成一个逆序对,请打印所有逆序对。
只要涉及数组中,两两比较,再进行操作的,都可以用归并排序。
基础第二课题目六:荷兰国旗问题
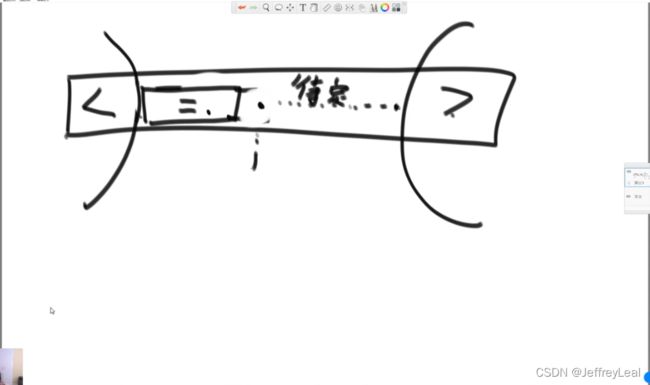
![]()

小于区域不断往右扩展,遇到比num大的数,就与未比较的区域的数交换,把大于num的数扔到右边,直到小于区域与右边的大于区域相遇。
基础第二课题目七:快速排序
1.0版本,用上面问题一和递归的结合

2.0版本,用上面问题二(荷兰国旗问题)和递归的结合
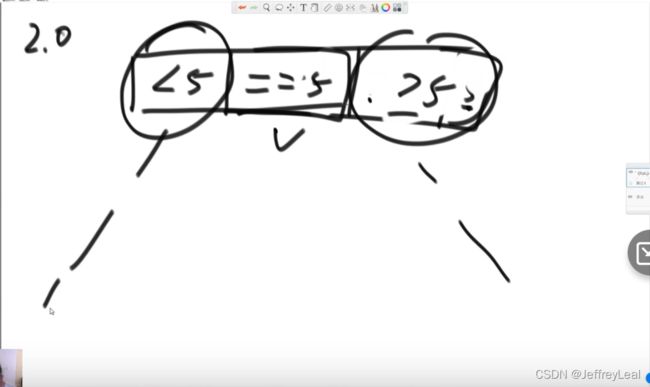
1.0,2.0版本,都有可能遇到划分的极端情况,左边区域很大,右边很小,复杂度就为 O ( N 2 ) O(N^2) O(N2)。
3.0版本,随机选择一个数来划分,那个极端好和极端坏的情况都是等概率事件,复杂度与概率求期望,得到期望复杂度为 O ( N log N ) O(N\log N) O(NlogN)。
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int l, int r) {
if (l < r) {
//将末位数字随机打乱
swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
int[] p = partition(arr, l, r);
quickSort(arr, l, p[0] - 1);
quickSort(arr, p[1] + 1, r);
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);//把当前数归到less区域
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);//把当前数归到more区域
} else {
l++;//推着equal区域右移
}
}
swap(arr, more, r);//把num放到equal区域
return new int[] { less + 1, more };//返回less区域和equal区域的边界,equal区域和more区域的边界
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
P4 3.详解桶排序以及排序内容大总结
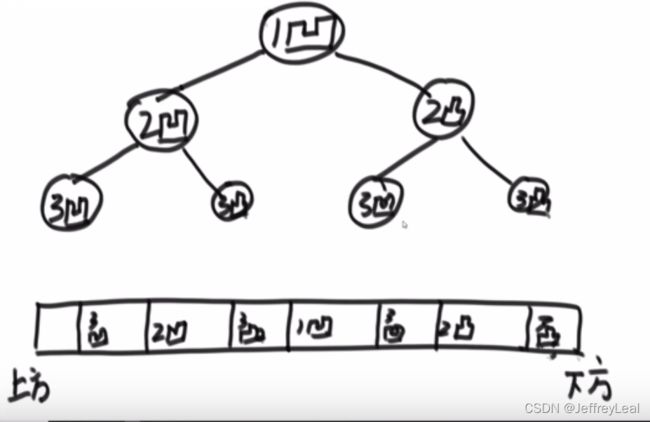
不完全二叉树示例:
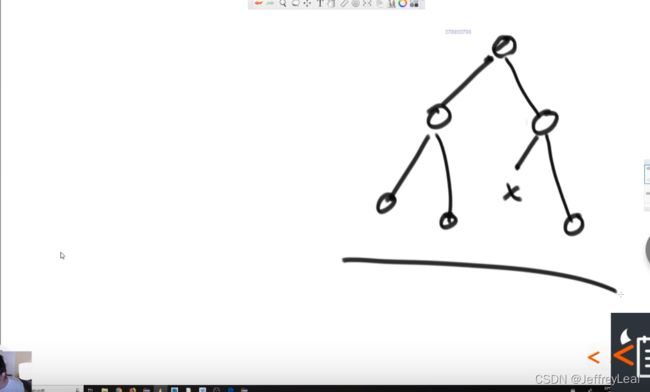
二叉树结构:

大根堆:父节点的数比子节点的数要大,示例:

利用![]()
新进堆的数与父节点比较,形成大根堆
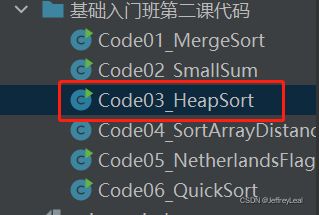
把新的数插入到堆中,就是上移:
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {//当前节点数值大于父节点位置
swap(arr, index, (index - 1) /2);
index = (index - 1)/2 ;
}
}
某数a在index位置,将其往下移动,至堆结构符合大根堆要求,,就是下移:
//某数a在index位置,将其往下移动
public static void heapify(int[] arr, int index, int size) {//size为数组长度
int left = index * 2 + 1;//左孩子位置
while (left < size) {//判断孩子是否存在
//只有当右孩子存在且大于左孩子时,才取右孩子作为最大值;
//其余情况选左孩子,包括
// 1.右孩子不存在
// 2.右孩子存在但没左孩子大
//largest记录最大值的位置
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
//比较父节点和大孩子之间谁大,记录下大的值的位置
largest = arr[largest] > arr[index] ? largest : index;
//如果父节点比较大,堆结构排好,退出
if (largest == index) {
break;
}
//孩子比较大,交换父和孩子的位置
swap(arr, largest, index);
//记录某数a的新位置
index = largest;
//记录处于新位置的某数a的左孩子
left = index * 2 + 1;
}
}
新增一个数,或删除最大值,调整的复杂度都是 O ( log N ) O(\log N) O(logN)。
用大根堆来排序:
所有数字先入大根堆,然后将最大数字于heapsize最后一个元素交换,heapsize减一,然后第一个数做heapify的下移操作,如此反复,就能将全部数字排序,调整的复杂度都是 O ( N log N ) O(N\log N) O(NlogN)。

public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//将所有数字搞成大根堆
for (int i = 0; i < arr.length; i++) {// O(N)
heapInsert(arr, i);// O(logN)
}
int size = arr.length;
//0位置上的数与heapsize最后一个数交换
swap(arr, 0, --size);
while (size > 0) {// O(N)
//0位置上的数重新调整位置
heapify(arr, 0, size);// O(logN)
//0位置上的数与heapsize最后一个数交换,heapsize减小
swap(arr, 0, --size);// O(1)
}
}
第一步,全部数字变成大根堆,有优化做法,最小的树做heapify,然后次小…:
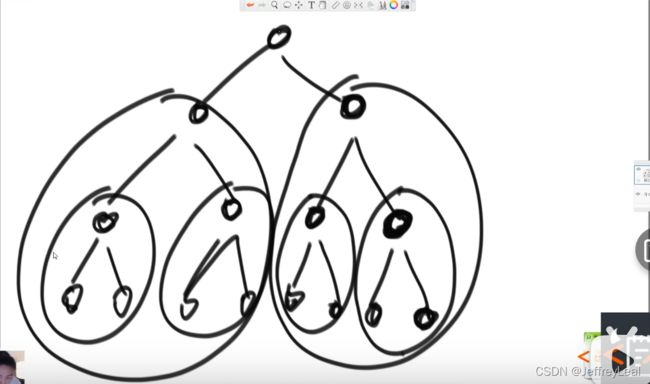
假设最底层代价是1,倒数第二层代价是二,如此类推:
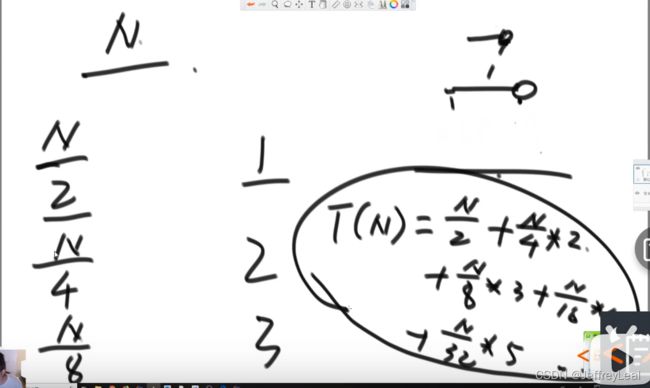
复杂度使用错位相加法:

最终复杂度为 O ( N ) O( N) O(N)。
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//将所有数字搞成大根堆
//做法1:
// for (int i = 0; i < arr.length; i++) {// O(N)
// heapInsert(arr, i);// O(logN)
// }
//做法2:
for (int i = arr.length-1; i >= 0 ; i--) {
heapify(arr, i, arr.length);
}
int size = arr.length;
//0位置上的数与heapsize最后一个数交换
swap(arr, 0, --size);
while (size > 0) {// O(N)
//0位置上的数重新调整位置
heapify(arr, 0, size);// O(logN)
//0位置上的数与heapsize最后一个数交换,heapsize减小
swap(arr, 0, --size);// O(1)
}
}
基础第二课题目五:堆排序扩展题目

因为0位置上的正确数一定在0-6这七个数中,所以将这7个数在小根堆中排好序,最小值就可以弹出放到0位置上,然后再加入下一个数,进行重复操作。复杂度为 O ( N log k ) O( N\log k) O(Nlogk)。
public static void main(String[] args) {
PriorityQueue<Integer> heap = new PriorityQueue<>();
heap.add(8);
heap.add(3);
heap.add(6);
heap.add(2);
heap.add(4);
while (!heap.isEmpty()){
System.out.println(heap.poll());
}
}
输出
2
3
4
6
8
Process finished with exit code 0
public void sortedArrDistanceLessK(int[] arr, int k) {
PriorityQueue<Integer> heap = new PriorityQueue<>();
int index = 0;
//k个数形成小根堆
for (; index < Math.min(arr.length, k); index++) {
heap.add(arr[index]);
}
int i = 0;
for (; index < arr.length; i++, index++) {
heap.add(arr[index]);//加一个数
arr[i] = heap.poll();//弹出一个最小值
}
while (!heap.isEmpty()) {//依次弹出k个最小值
arr[i++] = heap.poll();
}
}
小根堆会遇到不够空间时扩容,扩容就会复制一次,长度为多少,复杂度就为多少,一共扩容 logN 次,总扩容复杂度为 O ( N log N ) O( N\log N) O(NlogN),均摊下来每个元素,复杂度为 O ( log N ) O( \log N) O(logN)。
系统提供的堆,只能给一个数,弹出一个数,不能做到上述的高效操作,要实现有高效操作的,必须自己写。
基础第三课题目二:桶排序
基于词频,频率的统计,然后还原成有序的数组:

计数排序:

基数排序:
先按个位数放进桶,然后从左往右,先进先出导出,再按十位数排序,重复,再按百位
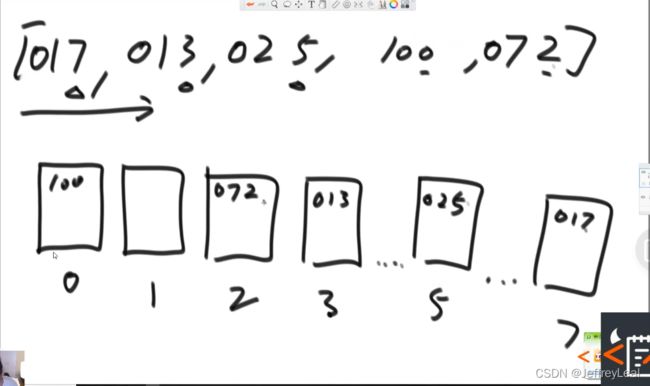
2:22:00开始看,代码的实现count不是记录桶 i i i 里面有多少个数,而是记录 ≤ i \leq i ≤i 里面有多少个数。
// only for no-negative value
public static void radixSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
//计算最大的十进制位是第几位
public static int maxbits(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);//寻找数组中最大的数
}
int res = 0;
while (max != 0) {
res++;
max /= 10;//自动整除,因为max是int
}
return res;
}
public static void radixSort(int[] arr, int begin, int end, int digit) {
final int radix = 10;
int i = 0, j = 0;
int[] bucket = new int[end - begin + 1];
//digit多少哥十进制位,也代表入桶出桶的次数
for (int d = 1; d <= digit; d++) {
int[] count = new int[radix];
//用于记录当前位上等于0,...,等于9的各有多少个数
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);//确认当位上的数是多少
count[j]++;//等于该位上的数,统计加1
}
//用于记录当前位上小于等于0,...,小于等于9的各有多少个数
//同时也记录了当前位上等于0,...,等于9的数组最后一个数出桶后的位置
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];//出桶后的位置上放该数
count[j]--;//该桶上的数减一
}
for (i = begin, j = 0; i <= end; i++, j++) {
//把bucket的数组导入arr中,相当于保留了这次桶排序
arr[i] = bucket[j];
}
}
}
P5 4.链表
基础第三课题目三:排序算法的稳定性及其汇总
不具备稳定性的例子:选择排序
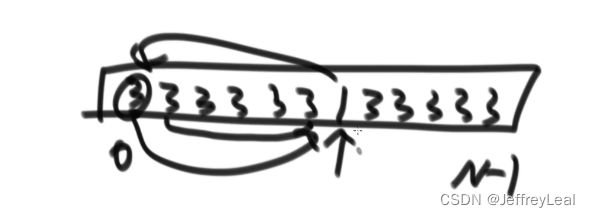
快速排序:
![]()
只要有跨度的交换,就会丧失稳定性。
相邻交换的则不会。
具备稳定性的例子:冒泡排序

插入排序:

归并排序关键在于merge的时候,要先拷贝左边的数,而用归并解决小和问题的时候,要先拷贝右边的数,则丧失稳定性:


总结
![]()
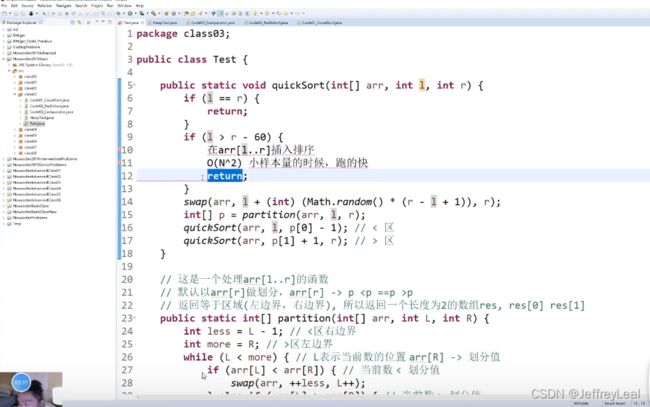
下面都是没有必要的**改进


在快速排序中,当样本量小于60的时候,插入排序时间复杂度相当,当常数操作复杂度极低,因此可以将2种混合起来。
基础第四课题目一:哈希表的简单介绍
hashset 和 hashmap

String、Integer这些都算基础类型。
基础第四课题目二:有序表的简单介绍



把列表扔到栈,然后弹出一个比对一个
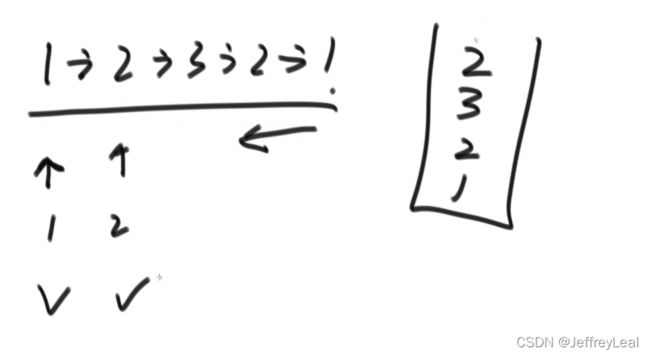
使用快慢指针,快指针结束的时候,慢指针走到中点。这个coding要练熟。
// need O(1) extra space
public static boolean isPalindrome3(Node head) {
if (head == null || head.next == null) {
return true;
}
Node n1 = head;//慢指针
Node n2 = head;//快指针
//快慢指针找末尾和中点
while (n2.next != null && n2.next.next != null) { // find mid node
n1 = n1.next; // n1 -> mid
n2 = n2.next.next; // n2 -> end
}
n2 = n1.next; // n2 -> right part first node
n1.next = null; // mid.next -> null
Node n3 = null;//用于记录n2原本的下一个node
//右半部分逆序
while (n2 != null) { // right part convert
n3 = n2.next; // n3 -> save next node,保留未改变的链表
n2.next = n1; // next of right node convert,改变链表指向
//n1,n2两个指针完成改变指向操作后,同时右移,准备下一个元素的链表指向逆序
n1 = n2; // n1 move
n2 = n3; // n2 move
}
n3 = n1; // n3 -> save last node
n2 = head;// n2 -> left first node
boolean res = true;
while (n1 != null && n2 != null) { // check palindrome
//每走一步,都验证
if (n1.value != n2.value) {
res = false;
break;
}
//n1,n2从中间开始走
n1 = n1.next; // left to mid
n2 = n2.next; // right to mid
}
n1 = n3.next;
n3.next = null;
//最后将逆序的链表变回来
while (n1 != null) { // recover list
n2 = n1.next;
n1.next = n3;
n3 = n1;
n1 = n2;
}
return res;
}
基础第四课题目九:按某值划分单向链表

笔试:创建node数组,把链表的node烤进去,再做partition,快速排序,即归并的3.0版本。
面试:使用6个变量指针,小于区域的头和尾,等于区域的头和尾,大于区域的头和尾,最后将3个区域连起来的时候,要注意是否有区域为空。

public static Node listPartition2(Node head, int pivot) {
Node sH = null; // small head
Node sT = null; // small tail
Node eH = null; // equal head
Node eT = null; // equal tail
Node bH = null; // big head
Node bT = null; // big tail
Node next = null; // save next node
// every node distributed to three lists
while (head != null) {
next = head.next;
head.next = null;
if (head.value < pivot) {
if (sH == null) {
sH = head;
sT = head;
} else {
sT.next = head;
sT = head;
}
} else if (head.value == pivot) {
if (eH == null) {
eH = head;
eT = head;
} else {
eT.next = head;
eT = head;
}
} else {
if (bH == null) {
bH = head;
bT = head;
} else {
bT.next = head;
bT = head;
}
}
head = next;
}
// small and equal reconnect
if (sT != null) {
sT.next = eH;
eT = eT == null ? sT : eT;
}
// all reconnect
if (eT != null) {
eT.next = bH;
}
return sH != null ? sH : eH != null ? eH : bH;
}
基础第四课题目十:复制含有随机指针节点的链表

做法1:第一次遍历旧链表,使用哈希map,key为旧链表,value为新链表,新链表只是单纯地串起来并拷贝int value值,rand没有设置;第二次遍历旧链表,调用key-value,设置rand node。
做法2:第一次遍历旧链表,不用哈希map,在旧map中,插入克隆node,拷贝int value值;第二次遍历链表,一对一对处理,设置rand node;第三次遍历,把旧节点删除。省去了hashmap的空间。

P6 5.二叉树
基础第四课题目十一:两个单链表相交

leetcode142题。
判断有环还是无环:
使用额外空间方法:使用hashset,把元素放进集合,判断是否存在;
不使用额外空间的方法:使用快慢指针,快指针走到空,就是无环,快慢指针相遇,就是有环。快慢指针第一次相遇之后,将快指针重置由头开始,慢指针在相遇处,同时再次出发,相遇的地方,就是环的入口。


判断环入口节点代码:
//获取环的入口
public static Node getLoopNode(Node head) {
if (head == null || head.next == null || head.next.next == null) {
return null;
}
Node n1 = head.next; // n1 -> slow
Node n2 = head.next.next; // n2 -> fast
while (n1 != n2) {
//判断快指针是否走完
if (n2.next == null || n2.next.next == null) {
return null;
}
n2 = n2.next.next;
n1 = n1.next;
}
n2 = head; // n2 -> walk again from head
while (n1 != n2) {
n1 = n1.next;
n2 = n2.next;
}
return n1;
}
情况1:2个链表都是无环,只可能是2条线,或者y型线,不可能是x型,x型就是节点处next指针指向2个地方,这是不可能的。2个链表如果相交,那么他们end端一定是地址一样的,2个链表都遍历。如果相交,要找到节点处,长的列表先走 ∣ l e n l o n g − l e n s h o r t ∣ |len_{long}-len_{short}| ∣lenlong−lenshort∣ 步,然后一起走,一定会在交点处相遇。
public static Node noLoop(Node head1, Node head2) {
if (head1 == null || head2 == null) {
return null;
}
Node cur1 = head1;
Node cur2 = head2;
int n = 0;//用于记录长度,先记录链表1长度,然后
//减去链表2的长度,差值的绝对值,就是长度差值
while (cur1.next != null) {
n++;
cur1 = cur1.next;
}
while (cur2.next != null) {
n--;
cur2 = cur2.next;
}
if (cur1 != cur2) {
return null;
}
cur1 = n > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
n = Math.abs(n);
while (n != 0) {//长链表先走差值步
n--;
cur1 = cur1.next;
}
while (cur1 != cur2) {
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
}
情况2:一个为无环,一个有环,那么必然不想交;
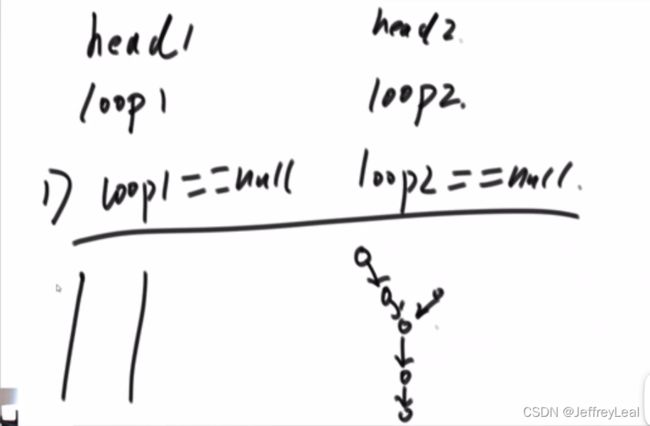
情况3:2个都是有环,又分3种情况:
情况3-1:2个不同的有环;
情况3-2:入环节点是同一个,最好判断,分别找到入环节点,如果入环节点不同就是情况3-1或者3-3,如果入环节点相同,就使用上面的无环代码去找相交节点;
情况3-3:入环节点不是同一个;让loop1继续走,在走会自己之前,判断会不会遇到loop2这个入口节点,遇到就是情况3-3,没有就是情况3-1;
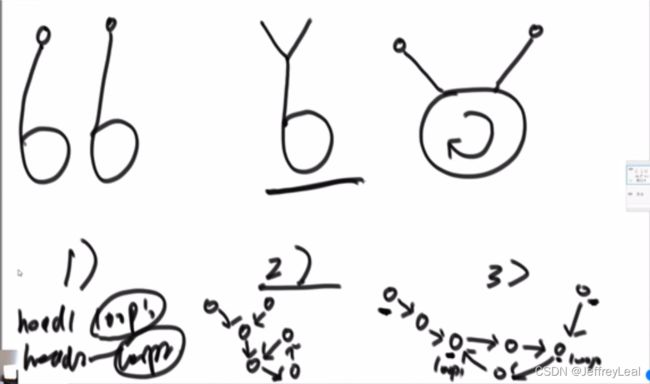
//两个有环链表。返回第一个相交节点,如果不想交返回null
//loop1,loop2分别为2个链表的环入口处节点
public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
Node cur1 = null;
Node cur2 = null;
if (loop1 == loop2) {//如果入环节点相同,是情况3-2
cur1 = head1;
cur2 = head2;
int n = 0;
while (cur1 != loop1) {
n++;
cur1 = cur1.next;
}
while (cur2 != loop2) {
n--;
cur2 = cur2.next;
}
cur1 = n > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
n = Math.abs(n);
while (n != 0) {
n--;
cur1 = cur1.next;
}
while (cur1 != cur2) {
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
} else {//如果入环节点不同,是情况3-1或3-3
cur1 = loop1.next;
while (cur1 != loop1) {
if (cur1 == loop2) {
return loop1;//情况3-3
}
cur1 = cur1.next;
}
return null;//情况3-1
}
}
基础第五课题目一:二叉树节点结构

1:06:00附近解释先序中序后续,遍历会3次遇到同一个节点,第几次遇到时打印,就是什么序。
更详细的可以看代码随想录 刷题攻略 二叉树 笔记
递归代码:
//先序遍历
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
//中序遍历
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
//后序遍历
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
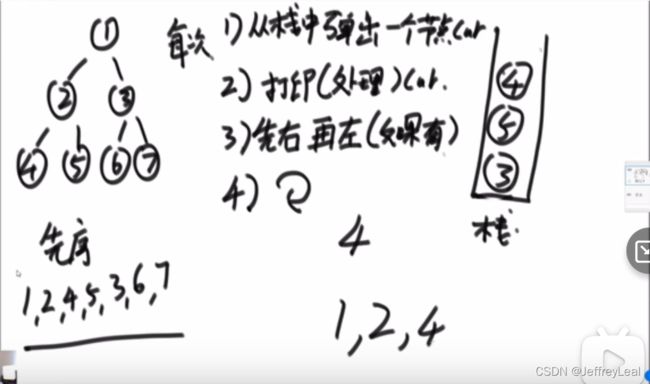
//非递归先序遍历,头左右的顺序
public static void preOrderUnRecur(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
//1.弹出一个节点
head = stack.pop();
System.out.print(head.value + " ");
//2.往栈加入节点,先右子节点后左子节点(如果有)
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
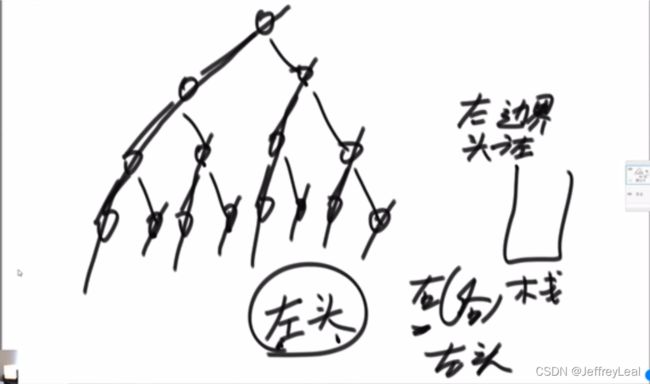
//非递归中序遍历,左头右的顺序
public static void inOrderUnRecur(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
//1.所有的左子节点全部进栈
stack.push(head);
head = head.left;
} else {
//2.弹出栈一个节点,如果有右子节点,对右子节点周而复始上述操作
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
//非递归后序遍历,左右头的顺序
public static void posOrderUnRecur1(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();//收集栈
s1.push(head);
while (!s1.isEmpty()) {
//1.从s1弹出一个节点,放入收集站s2
head = s1.pop();
s2.push(head);
//2.先压左子节点进收集站,后压右子节点进收集站
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}

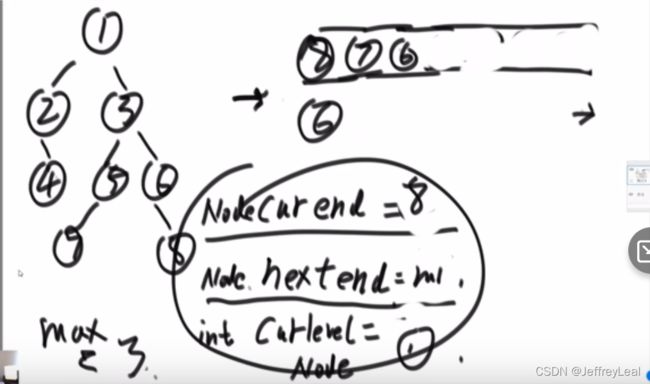
也叫层次遍历,使用队列而不是栈,队列是先进先出。
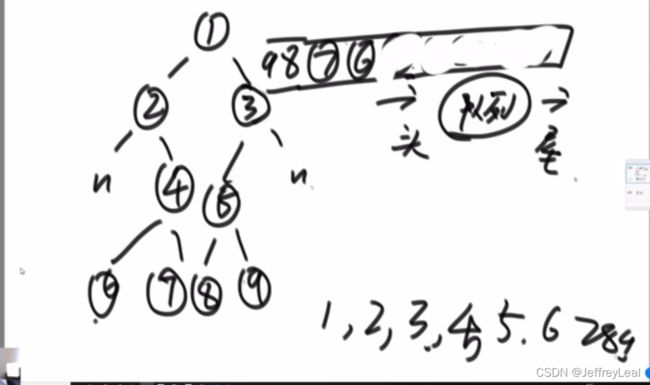
1:58:30附近,求最大宽度,方法1,使用hashmap

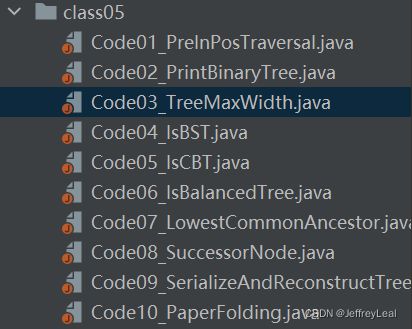
对于二叉树来说,深度优先遍历就是先序遍历
P7 6. 图
基础第五课题目二:二叉树的相关概念及其实现判断
判断是否搜索二叉树
搜索二叉树,每个节点的左子节点及其子树都比自己小,右子节点及其子树都比自己大:
中序遍历,结果升序,就是搜索二叉树。把中序遍历的打印操作换成比较值的大小。
public static boolean isBST(Node head) {
if (head == null) {
return true;
}
LinkedList<Node> inOrderList = new LinkedList<>();
//保留中序次序
process(head, inOrderList);
int pre = Integer.MIN_VALUE;
//遍历中序次序,看是否由小到大
for (Node cur : inOrderList) {
if (pre >= cur.value) {
return false;
}
pre = cur.value;
}
return true;
}
//递归中序遍历,把原来的打印换成把节点添加到新列表,保留中序次序
public static void process(Node node, LinkedList<Node> inOrderList) {
if (node == null) {
return;
}
process(node.left, inOrderList);
inOrderList.add(node);
process(node.right, inOrderList);
}
使用黑盒递归套路:
![]()
先更新最大最小值,再做违规判断,返回true or false:
//黑盒子方法套路判断是否是搜索二叉树
public static boolean isBST1(Node head) {
return process(head).isBST;
}
//由于递归的返回值有3个,所有要构造一个类接受这3个返回值
public static class ReturnType {
public boolean isBST;//是否是搜索二叉树
public int min;
public int max;
public ReturnType(boolean isBST, int min, int max) {
this.isBST = isBST;
this.min = min;
this.max = max;
}
}
public static ReturnType process(Node x) {
if (x == null) {//base情况,空节点的返回值
return null;
}
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
int min = x.value;
int max = x.value;
//先用子树的最大最小值更新此节点的最大最小值
if(leftData != null){
min = Math.min(min,leftData.min);
max = Math.max(max,leftData.max);
}
if(rightData != null){
min = Math.min(min,rightData.min);
max = Math.max(max,rightData.max);
}
boolean isBST = true;
//判断子树是否违规,违规条件:
//违规情况1:左子树存在,且它的最大值大于父节点或者
//左子树不是搜索二叉树
if(leftData != null &&(!leftData.isBST || leftData.max >= x.value)){
isBST = false;
}
//违规情况2:右子树存在,且它的最小值小于父节点或者
//右子树不是搜索二叉树
if(rightData != null &&(!rightData.isBST || rightData.max <= x.value)){
isBST = false;
}
return new ReturnType(isBST, min,max);
}
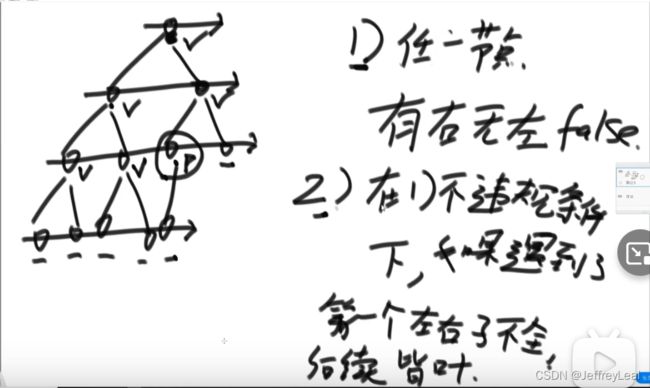
判断是否完全二叉树
//按宽度遍历,即按层遍历
public static boolean isCBT(Node head) {
if (head == null) {
return true;
}
LinkedList<Node> queue = new LinkedList<>();
boolean leaf = false;//用来记录是否出现过某个节点左右子节点不全的情况
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
if (
//情况二,在不违反情况一的条件下,在首次出现
//某个节点左右子节点不全的情况后,后续节点必
//须都是叶节点,如果不满足,则返回false
(leaf && (l != null || r != null))
||
//情况一:右节点存在,左节点不存在,返回false
(l == null && r != null)) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
} else {
//情况二,在不违反情况一的条件下,在首次出现
//某个节点左右子节点不全的情况后,标记事件
leaf = true;
}
}
return true;
}
判断是否是满二叉树
判断是否是平衡二叉树
定义:任何一棵子树,它的左树高度和右树高度的高度差不能超过1

使用黑盒递归套路:列举判断条件,从子树收集信息
public static boolean isBalanced(Node head) {
return process(head).isBalanced;
}
//由于递归的返回值有2个,所有要构造一个类接受这两个返回值
public static class ReturnType {
public boolean isBalanced;//是否是平衡二叉树
public int height;//高度多少
public ReturnType(boolean isB, int hei) {
isBalanced = isB;
height = hei;
}
}
public static ReturnType process(Node x) {
if (x == null) {//base情况,空节点的返回值
return new ReturnType(true, 0);
}
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
int height = Math.max(leftData.height, rightData.height);
boolean isBalanced =
//左树是平衡二叉树
leftData.isBalanced
&&
//右树是平衡二叉树
rightData.isBalanced
&&
//左右子树高度差不超过1
Math.abs(leftData.height - rightData.height) < 2;
return new ReturnType(isBalanced, height);
}
树形DP
只要从左树右树获取信息,大部分可以用这个套路来解。
基础第五课题目三:二叉树的公共祖先
// 方法1,思路抽象,只有2种情况
// 情况1:o1为o2的祖先,或o2为o1的祖先
// 情况2:都不是对方的祖先
public static Node lowestAncestor(Node head, Node o1, Node o2) {
// head == null 是base情况,其余情况遇到o1返回o1,遇到
// o2返回o2
if (head == null || head == o1 || head == o2) {
return head;
}
// 下面2行的返回值只可能是null、o1、o2
Node left = lowestAncestor(head.left, o1, o2);
Node right = lowestAncestor(head.right, o1, o2);
// 左右2边返回值都是null,说明子节点没有o1,o2,所以返回head
if (left != null && right != null) {
return head;
}
// 2个节点不都为空的情况,左边不为空返回左边,左边为空返回右边
return left != null ? left : right;
}
// 方法2,思路简单
public static class Record1 {
private HashMap<Node, Node> map;
public Record1(Node head) {
map = new HashMap<Node, Node>();
if (head != null) {
//把头结点也放到hashmap中
map.put(head, null);
}
setMap(head);
}
//遍历,记录每个节点的父节点,放到hashmap中
private void setMap(Node head) {
if (head == null) {
return;
}
if (head.left != null) {
map.put(head.left, head);
}
if (head.right != null) {
map.put(head.right, head);
}
setMap(head.left);
setMap(head.right);
}
public Node query(Node o1, Node o2) {
HashSet<Node> path = new HashSet<Node>();
//把o1节点及其父节点全部放到新的hashmap中
while (map.containsKey(o1)) {
path.add(o1);
o1 = map.get(o1);
}
//检查o2及其父节点是否在新的hashmap中,在则是公共祖先
while (!path.contains(o2)) {
o2 = map.get(o2);
}
return o2;
}
}
基础第五课题目四:二叉树的后继节点

后继节点:中序遍历中,一个点的下一个节点就是后继节点。
前驱节点与其相反。
此node类型具有指向父节点的指针。
中序遍历的复杂度为 O ( N ) O(N) O(N),但希望可以优化成 O ( k ) O(k) O(k),k为2个点在树上的距离。
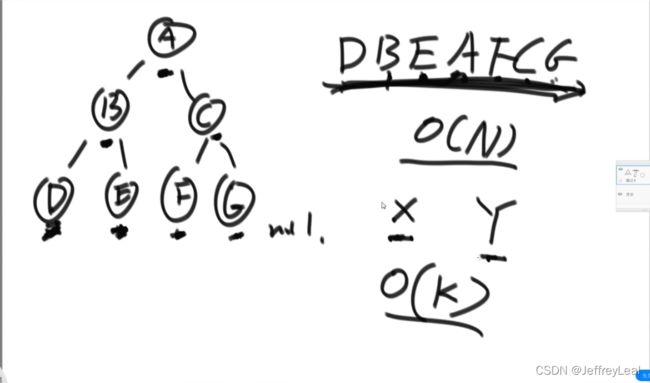
后继节点的2种情况:
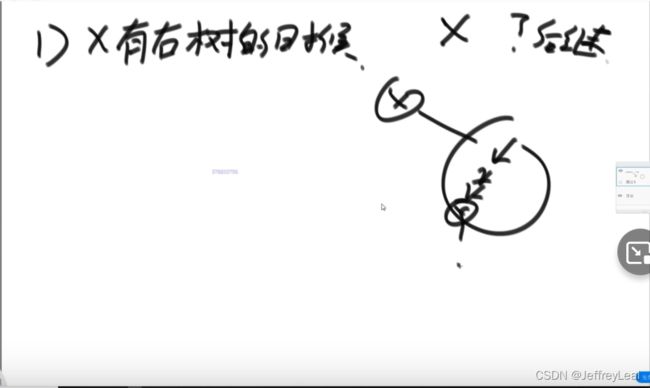

public static Node getSuccessorNode(Node node) {
if (node == null) {
return node;
}
if (node.right != null) {
//右子节点不为空,则后继节点必为右子节点子树的最左节点
return getLeftMost(node.right);
} else {
//右子节点为空,一直往上找父节点,直到父节点不为别人的右子节点
Node parent = node.parent;
while (parent != null && parent.left != node) {
node = parent;
parent = node.parent;
}
return parent;
}
}
public static Node getLeftMost(Node node) {
if (node == null) {
return node;
}
while (node.left != null) {
node = node.left;
}
return node;
}
基础第五课题目五:二叉树的序列化和反序列化
内存变成字符串叫序列化

先序遍历序列化示例:
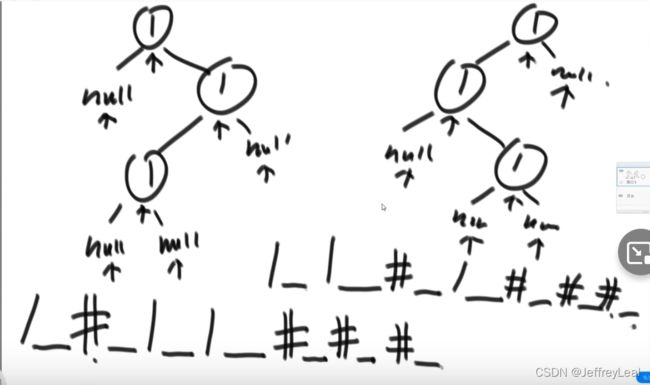
先序遍历反序列化
怎么样遍历序列化,就怎么样遍历反序列化
//先序遍历序列化
public static String serialByPre(Node head) {
if (head == null) {
return "#!";
}
String res = head.value + "!";
res += serialByPre(head.left);
res += serialByPre(head.right);
return res;
}
//先序遍历反序列化
public static Node reconByPreString(String preStr) {
String[] values = preStr.split("!");
Queue<String> queue = new LinkedList<String>();
for (int i = 0; i != values.length; i++) {
queue.offer(values[i]);
}
return reconPreOrder(queue);
}
public static Node reconPreOrder(Queue<String> queue) {
String value = queue.poll();
if (value.equals("#")) {
return null;
}
Node head = new Node(Integer.valueOf(value));
head.left = reconPreOrder(queue);
head.right = reconPreOrder(queue);
return head;
}
基础第五课题目六:折纸问题
public static void printProcess(int i, int N, boolean down) {
if (i > N) {
return;
}
printProcess(i + 1, N, true);
System.out.println(down ? "down " : "up ");
printProcess(i + 1, N, false);
}
public static void main(String[] args) {
int N = 1;
printAllFolds(N);
}
P8 7.详解前缀树和贪心算法
基础第六课题目一:图的存储方式
邻接表法表示无向图:
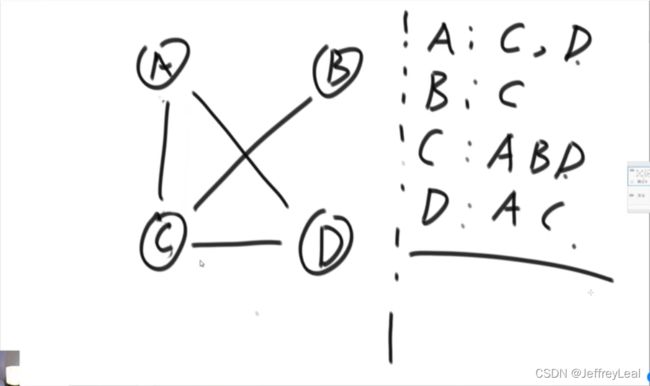
矩阵表法:
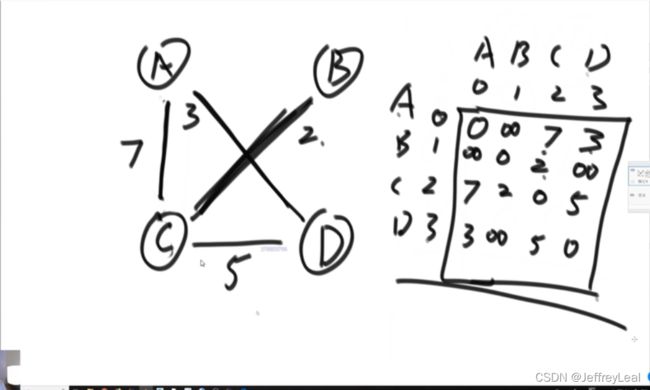
有向无环图:

图的难点在于:图的算法不难,但是图的结构有多种表达,在这类题的技巧在于,先用一种图结构a实现所有算法,把其他遇到的图结构转换成图结构a,在代入算法。
左神常用图结构:
public class Graph {
//integer 是索引
public HashMap<Integer,Node> nodes;
public HashSet<Edge> edges;
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
节点结构:
public class Node {
public int value;
public int in;//有多少个节点指向这个点
public int out;//这个点指向有多少个其他点
public ArrayList<Node> nexts;
public ArrayList<Edge> edges;
public Node(int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}
边的结构:无向边只要2个反向边一拼就可以了
public class Edge {
public int weight;//边的长度
public Node from;
public Node to;
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}
图接口的实现:
public class GraphGenerator {
//matrix的每一行结构为:源城市编号,目标城市编号,距离
//将它转换为我的图结构表示
public static Graph createGraph(Integer[][] matrix) {
Graph graph = new Graph();
for (int i = 0; i < matrix.length; i++) {
Integer weight = matrix[i][0];//距离
Integer from = matrix[i][1];//源城市编号
Integer to = matrix[i][2];//目标城市编号
if (!graph.nodes.containsKey(from)) {
//如果源城市第一次出现,则加入到图中,创立新节点
graph.nodes.put(from, new Node(from));
}
if (!graph.nodes.containsKey(to)) {
//如果目标城市第一次出现,则加入到图中,创立新节点
graph.nodes.put(to, new Node(to));
}
Node fromNode = graph.nodes.get(from);//源城市节点
Node toNode = graph.nodes.get(to);//目标城市节点
//创建源城市与目标城市之间的边
Edge newEdge = new Edge(weight, fromNode, toNode);
//完善源城市节点信息
fromNode.nexts.add(toNode);
fromNode.out++;
fromNode.edges.add(newEdge);
//完善目标城市节点信息
toNode.in++;
//完善图结构信息
graph.edges.add(newEdge);
}
return graph;
}
}
基础第六课题目二:优先遍历
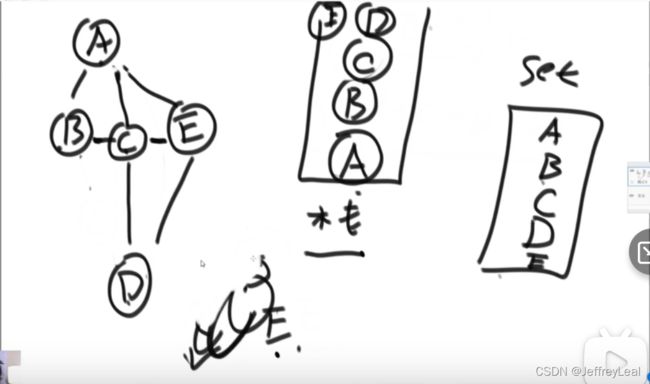
图的宽度优先遍历
public static void bfs(Node node) {
if (node == null) {
return;
}
//用来储存所有节点
Queue<Node> queue = new LinkedList<>();
//确保上面的队列储存的节点不要重复
HashSet<Node> map = new HashSet<>();
queue.add(node);
map.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
for (Node next : cur.nexts) {
//不重复,则添加到队列和set中
if (!map.contains(next)) {
map.add(next);
queue.add(next);
}
}
}
}
广度优先遍历
基础第六课题目三:拓扑排序

解决依赖之间,有互相依赖的情况,哪一个优先编译

依次找到入度为0的点,把它和它的指向都擦掉,如此循环:

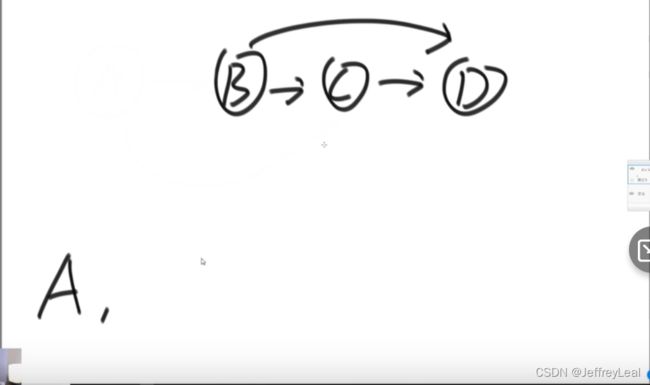
// directed graph and no loop
public static List<Node> sortedTopology(Graph graph) {
//记录节点,及其入度
HashMap<Node, Integer> inMap = new HashMap<>();
//收集当前入度为0的节点
Queue<Node> zeroInQueue = new LinkedList<>();
for (Node node : graph.nodes.values()) {
inMap.put(node, node.in);
if (node.in == 0) {
zeroInQueue.add(node);
}
}
//记录节点输出顺序
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
//弹出一个当前入度为0的节点
Node cur = zeroInQueue.poll();
//加入到输出中
result.add(cur);
//将此节点的指向全部擦去,指向的节点入度全部减一
for (Node next : cur.nexts) {
inMap.put(next, inMap.get(next) - 1);
//若入度减一后变为入度为0的节点,加入到收集队列中
if (inMap.get(next) == 0) {
zeroInQueue.add(next);
}
}
}
return result;
}
基础第六课题目四:kruskal算法

和prim功能一样,但出发点不同,kruskal从边的角度出发
消除多余的边,同时保证连通性
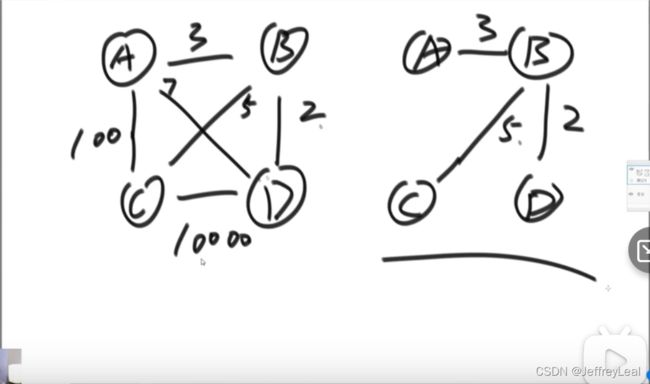
从最小的边开始考虑,加上这条边,看有没有形成环,有环就不加,没环就保留。
查看有没有环:集合查询和集合合并的机制,使用并查集

1:37:00附近
// Union-Find Set
public static class UnionFind {
private HashMap<Node, Node> fatherMap;
private HashMap<Node, Integer> rankMap;
public UnionFind() {
fatherMap = new HashMap<Node, Node>();
rankMap = new HashMap<Node, Integer>();
}
private Node findFather(Node n) {
Node father = fatherMap.get(n);
if (father != n) {
father = findFather(father);
}
fatherMap.put(n, father);
return father;
}
public void makeSets(Collection<Node> nodes) {
fatherMap.clear();
rankMap.clear();
for (Node node : nodes) {
fatherMap.put(node, node);
rankMap.put(node, 1);
}
}
public boolean isSameSet(Node a, Node b) {
return findFather(a) == findFather(b);
}
public void union(Node a, Node b) {
if (a == null || b == null) {
return;
}
Node aFather = findFather(a);
Node bFather = findFather(b);
if (aFather != bFather) {
int aFrank = rankMap.get(aFather);
int bFrank = rankMap.get(bFather);
if (aFrank <= bFrank) {
fatherMap.put(aFather, bFather);
rankMap.put(bFather, aFrank + bFrank);
} else {
fatherMap.put(bFather, aFather);
rankMap.put(aFather, aFrank + bFrank);
}
}
}
}
//用于比较边长大小
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> kruskalMST(Graph graph) {
UnionFind unionFind = new UnionFind();
unionFind.makeSets(graph.nodes.values());
//此队列的作用是收集所有边,让边从小到大弹出
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
for (Edge edge : graph.edges) {
priorityQueue.add(edge);
}
Set<Edge> result = new HashSet<>();
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();
//如果这两个节点不在一个集合中,即没有形成环
if (!unionFind.isSameSet(edge.from, edge.to)) {
result.add(edge);
//把这两个节点放到一个集合中
unionFind.union(edge.from, edge.to);
}
}
return result;
}
基础第六课题目五:prim算法

和kruskal功能一样,但出发点不同,prim从node的角度出发
1:49:00附近
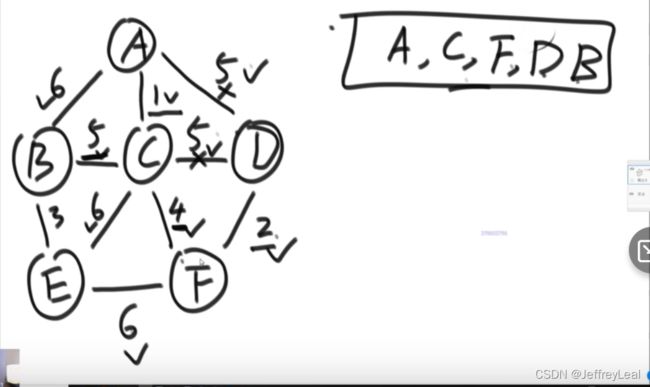
假设从A开始,解锁了3条边,然后选最小的,就到了C,再解锁4条边,选最小的,到F,解锁2条边,选最小,到D,没有解锁新边,从剩余已解锁的边选最小的,到B,解锁一条新的边,到E。
public static Set<Edge> primMST(Graph graph) {
// 把解锁的边放入小根堆,小根堆会从小到大将元素弹出,
// 定义个比较器,用于比较边的大小
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(
new EdgeComparator());
// 考察过的点都放入这个集合里面
HashSet<Node> set = new HashSet<>();
Set<Edge> result = new HashSet<>();
// values(),返回一个collection迭代器
// 这个for循环是为了解决多个连通区域不连通的问题
for (Node node : graph.nodes.values()) {//随便挑一个点开始
// 如果这个点没考察过,记录到集合中
if (!set.contains(node)) {
set.add(node);
// 遍历这个点的所有边,放入小根堆
for (Edge edge : node.edges) {
priorityQueue.add(edge);
}
while (!priorityQueue.isEmpty()) {
// 小根堆的边从小到大一次弹出
Edge edge = priorityQueue.poll();
Node toNode = edge.to;
// 看边指向的点是否考察过
if (!set.contains(toNode)) {
set.add(toNode);
result.add(edge);
for (Edge nextEdge : toNode.edges) {
priorityQueue.add(nextEdge);
}
}
}
}
}
return result;
}
基础第六课题目六:Dijkstra算法

用于记录一个点出发,到其他点的最小距离,可以使用小根堆的优化。

// 从head出发到所有点的最小距离
public static HashMap<Node, Integer> dijkstra1(Node head) {
// key : 从head出发到达key
// value : 从head出发到达key的最小距离
HashMap<Node, Integer> distanceMap = new HashMap<>();
// 头结点到自己的距离为0
distanceMap.put(head, 0);
// 求过距离的节点,存在selectedNodes中,以后再也不碰,锁住了
// head到selectedNode的距离不会再更新
HashSet<Node> selectedNodes = new HashSet<>();
// 一开始,所有节点都没锁,所以返回的节点必然是head
Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
while (minNode != null) {
int distance = distanceMap.get(minNode);
for (Edge edge : minNode.edges) {
Node toNode = edge.to;
// 如果head到tonode的距离从来没有计算过,那么距离就是head到
// 当前节点距离,加上当前节点到tonode距离
if (!distanceMap.containsKey(toNode)) {
distanceMap.put(toNode, distance + edge.weight);
}
// 如果head到tonode的距离计算过,那么距离就是(head到当前节点距离加上
// 当前节点到tonode距离),或者(head到tonode距离距离)之间较小的一个
distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
}
// 并将当前节点锁住
selectedNodes.add(minNode);
// 在没有被锁死的点中,再次找到离head距离最小的点
minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
}
return distanceMap;
}
// 在没有被锁死的点中,找到离head距离最小的点
public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap,
HashSet<Node> touchedNodes) {
Node minNode = null;
int minDistance = Integer.MAX_VALUE;// 距离正无穷
for (Entry<Node, Integer> entry : distanceMap.entrySet()) {
Node node = entry.getKey();
int distance = entry.getValue();
// 如果head节点到当前终点节点距离的计算没有被锁死,并且距离是最小
// 的,把这个点选出来,作为下一轮距离计算的起点
if (!touchedNodes.contains(node) && distance < minDistance) {
minNode = node;
minDistance = distance;
}
}
return minNode;
}
P9 8. 暴力递归
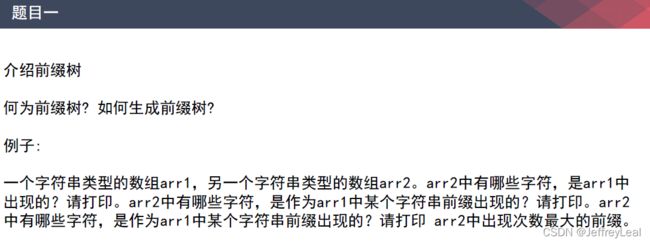
基础第七课题目一:前缀树
节点代码与视图
public static class TrieNode {
public int path;// 这个节点被通过了多少次
public int end;// 它是多少个字符串的结尾节点
public TrieNode[] nexts;// 它的下一个节点
public TrieNode() {
path = 0;
end = 0;
nexts = new TrieNode[26];
}
}

查询有没有某个字符串,hashset也可以做,但是以某个字符串为前缀的功能就完成不了了,前缀树就可以。如果next的种类特别多,可以用hashset。
public static class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
//添加新词
public void insert(String word) {
if (word == null) {
return;
}
char[] chs = word.toCharArray();
TrieNode node = root;
node.path++;
int index = 0;
for (int i = 0; i < chs.length; i++) {// 遍历字符
index = chs[i] - 'a';// 计算当前字符属于0-25哪条路径
if (node.nexts[index] == null) {//没有路径就新建路径
node.nexts[index] = new TrieNode();
}
// node变为路径上的下一个节点
node = node.nexts[index];
node.path++;
}
node.end++;
}
public void delete(String word) {
// 如果加入过这个词,才做删除
if (search(word) != 0) {
char[] chs = word.toCharArray();
TrieNode node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
// 如果在删除路径的过程中,遇到path为0了,后续路径
// 可以直接丢弃
if (--node.nexts[index].path == 0) {
node.nexts[index] = null;
return;
}
node = node.nexts[index];
}
node.end--;
}
}
public int search(String word) {
if (word == null) {
return 0;
}
char[] chs = word.toCharArray();
TrieNode node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
//到节点末端都没找到,就是加入了0次
if (node.nexts[index] == null) {
return 0;
}
node = node.nexts[index];
}
return node.end;
}
// 有多少哥词以pre为前缀
public int prefixNumber(String pre) {
if (pre == null) {
return 0;
}
char[] chs = pre.toCharArray();
TrieNode node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.nexts[index] == null) {
return 0;
}
node = node.nexts[index];
}
return node.path;
}
}
基础第七课题目二:贪心算法
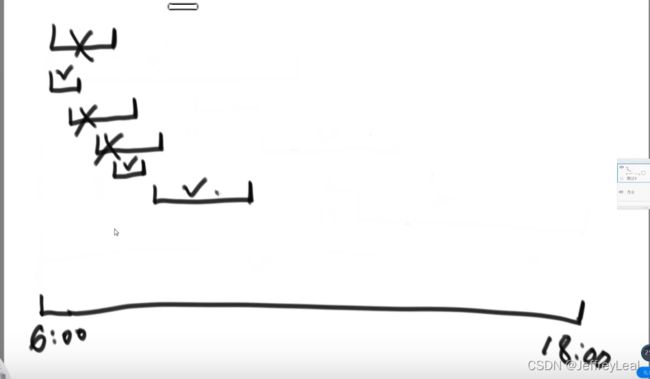
基础第七课题目七:会议室宣讲安排
public static int bestArrange(Program[] programs, int start) {
// 会议按结束时间,有小到大排列
Arrays.sort(programs, new ProgramComparator());
int result = 0;
for (int i = 0; i < programs.length; i++) {
// 看当前会议的开始时间有没有比上一个安排的会议结束时间
// 要晚,如果是,则安排此会议,并更新结束时间
if (start <= programs[i].start) {
result++;
start = programs[i].end;
}
}
return result;
}
public static void main(String[] args) {
}
基础第七课题目三:贪心算法解题套路
基础第七课题目四:字符串拼接题目证明
拼接运算变成数学运算
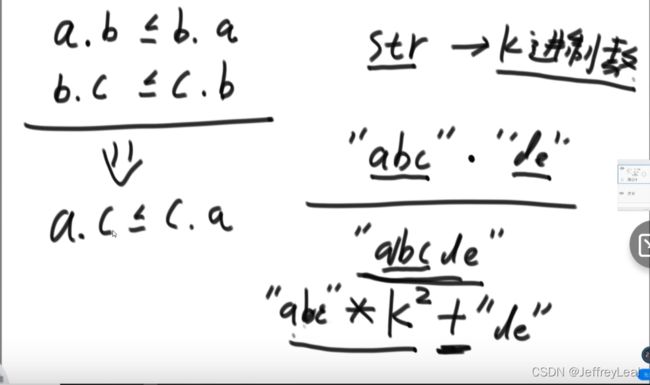
先证比较传递性

再证不挨着的2个字符串也能比较
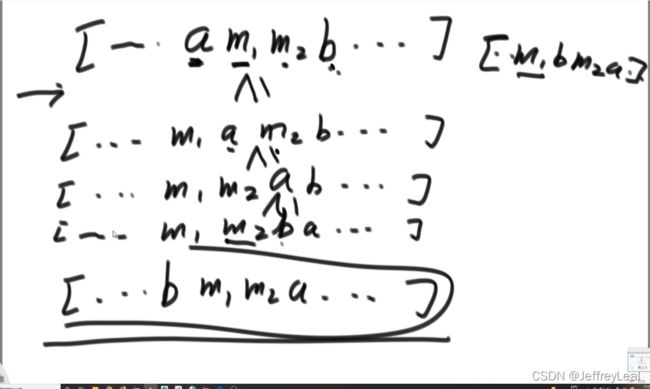
数学归纳法继续证明
基础第七课题目六:金条分割

哈夫曼树编码问题,小根堆弹出2个最小的数,重新放到小根堆中,重复此操作。
public static int lessMoney(int[] arr) {
PriorityQueue<Integer> pQ = new PriorityQueue<>();
// 放入小根堆中
for (int i = 0; i < arr.length; i++) {
pQ.add(arr[i]);
}
int sum = 0;
int cur = 0;
while (pQ.size() > 1) {
// 弹出最小的2个数,计算代价
cur = pQ.poll() + pQ.poll();
sum += cur;
// 将这2个数合并后重新放入小根堆
pQ.add(cur);
}
return sum;
}
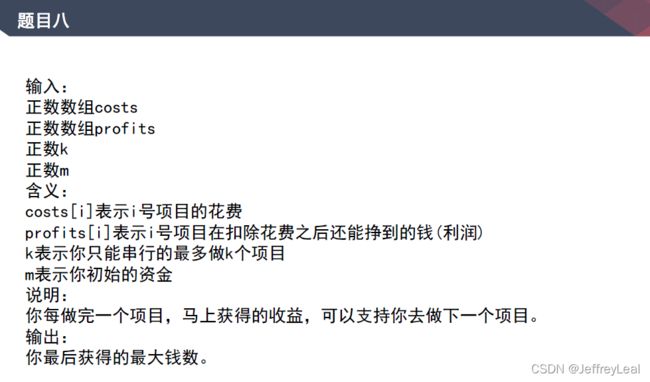
基础第七课题目八:银行家问题
花费与收益,按照花费放入小根堆,锁住花费大于M的项目,弹出花费小于M的项目,放入大根堆,按照利润排序,大根堆弹出利润最大的一个,更新M值,重复操作。
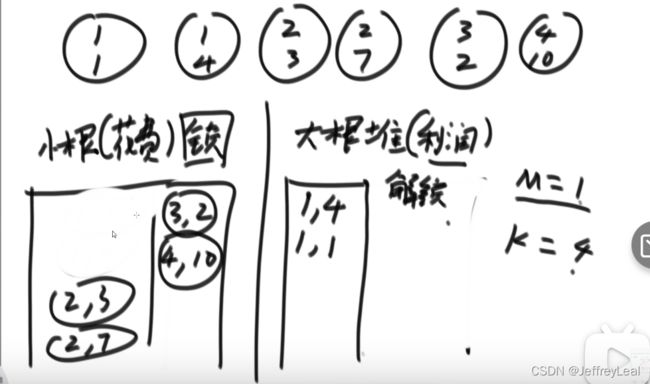
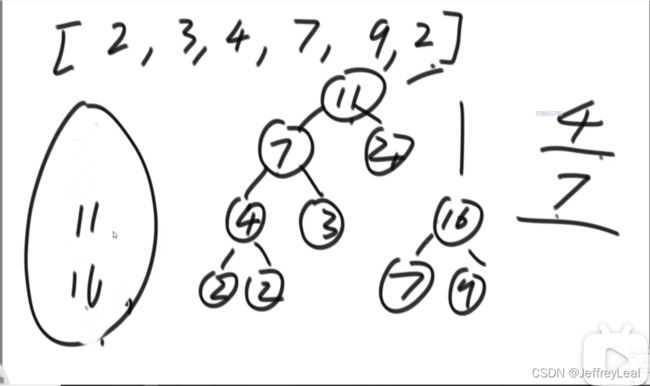
基础第七课题目九:找中位数
![]()
基础第八课题目九:N皇后问题
public static int num1(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n];
return process1(0, record, n);
}
// i:目前是第几行
// record:记录[0,...,i-1]行在第几列放皇后,并且符合题目要求
// n:棋盘一共多少行
// return:有多少种合理的摆法
public static int process1(int i, int[] record, int n) {
if (i == n) {// 来到终止行就代表找到了一种
return 1;
}
int res = 0;
// 遍历当前行的每个列位置作为起点,各有多少种
for (int j = 0; j < n; j++) {
// 判断当前列位置作为起点是否符合要求
if (isValid(record, i, j)) {
record[i] = j;
// 基于当前record作为起点,后续有多少种可能
res += process1(i + 1, record, n);
}
}
return res;
}
public static boolean isValid(int[] record, int i, int j) {
for (int k = 0; k < i; k++) {
if (j == record[k] // 共列
||
// 斜率的绝对值等于1就是共斜线
Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
复杂度为 O ( N N ) O(N^N) O(NN),只有常数时间可以优化。常数优化版本,使用位运算来优化。
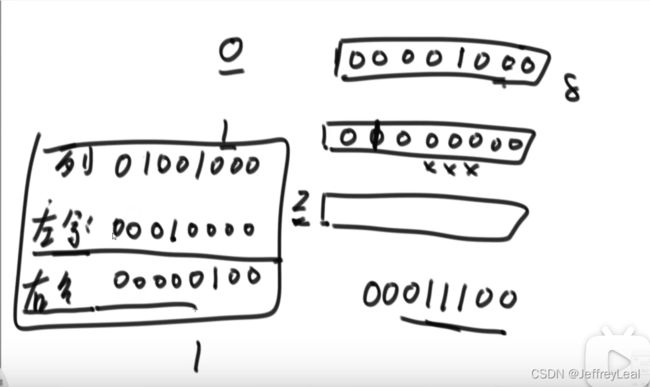
1皇后——32皇后问题,改进isValid()函数的判断,使用3个量表示下一行不能在哪个位置上填数,列位置,左对角线位置,右对角线位置。
pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));
public static int num2(int n) {
if (n < 1 || n > 32) {// 1皇后——32皇后问题
return 0;
}
// n皇后问题,就用n位2进制数表示下一行位置上的限制
// 位上为1代表能试
int upperLim = n == 32 ? -1 : (1 << n) - 1;
return process2(upperLim, 0, 0, 0);
}
public static int process2(int upperLim, int colLim, int leftDiaLim,
int rightDiaLim) {
if (colLim == upperLim) {// 所有皇后都填上了
return 1;
}
int pos = 0;
int mostRightOne = 0;
// pos 代表能填皇后的位置,与upperLim与运算为了屏蔽高位无关信息
// 位上为1代表能试
pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));
int res = 0;
while (pos != 0) {
mostRightOne = pos & (~pos + 1);// 提取最右位置上的1来填皇后
pos = pos - mostRightOne;// 提取完把那个位减掉
// 并将这个位加入到列限制,左对角线限制,右对角线限制中
res += process2(upperLim, colLim | mostRightOne,
(leftDiaLim | mostRightOne) << 1,
(rightDiaLim | mostRightOne) >>> 1);
}
return res;
}
P10 9. 补充视频
基础第六课题目六:Dijkstra算法补充
原本遍历来找最小值,可以用堆进行找最小值的优化,弹出最小值后,对堆里的数进行更新,要更新之后,仍保持堆的结构,就要修改堆的算法。
public static class NodeRecord {
public Node node;
public int distance;
public NodeRecord(Node node, int distance) {
this.node = node;
this.distance = distance;
}
}
public static class NodeHeap {
private Node[] nodes;
private HashMap<Node, Integer> heapIndexMap;// 节点在堆的位置
private HashMap<Node, Integer> distanceMap;// 节点的值
private int size; // 一共多少个节点
public NodeHeap(int size) {
nodes = new Node[size];
heapIndexMap = new HashMap<>();
distanceMap = new HashMap<>();
this.size = 0;
}
public boolean isEmpty() {
return size == 0;
}
public void addOrUpdateOrIgnore(Node node, int distance) {
// 如果点在堆中,没有被弹出
if (inHeap(node)) {
// 更新distance
distanceMap.put(node, Math.min(distanceMap.get(node), distance));
// 更新完之后,重新调整其在堆中的位置
insertHeapify(node, heapIndexMap.get(node));
}
// 如果点不在堆中,也从来没有进来过,则新建记录
// 如果点不在堆中,但进来过,就什么都不做,不执行下面代码
if (!isEntered(node)) {
// 新增这个点
nodes[size] = node;
heapIndexMap.put(node, size);
distanceMap.put(node, distance);
// 插入到应该有的位置
insertHeapify(node, size++);
}
}
public NodeRecord pop() {
// 记录弹出的节点及其距离
NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));
// 交换最大值和最小值位置
swap(0, size - 1);
// 该弹出的点,即最小值的点索引记为-1
heapIndexMap.put(nodes[size - 1], -1);
// 移除该节点
distanceMap.remove(nodes[size - 1]);
// 移除该节点
nodes[size - 1] = null;
// 将最大值重新插入
heapify(0, --size);
return nodeRecord;
}
private void insertHeapify(Node node, int index) {
while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {
swap(index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private void heapify(int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])
? left + 1 : left;
smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;
if (smallest == index) {
break;
}
swap(smallest, index);
index = smallest;
left = index * 2 + 1;
}
}
// node有没有进来过堆
private boolean isEntered(Node node) {
return heapIndexMap.containsKey(node);
}
// 点在不在堆中
private boolean inHeap(Node node) {
// 在堆中:曾经进来过,并且没有弹出
// 如果弹出了,就会将索引设置为-1
return isEntered(node) && heapIndexMap.get(node) != -1;
}
// 交换2个节点在堆中的位置
private void swap(int index1, int index2) {
// 先交换索引的位置
heapIndexMap.put(nodes[index1], index2);
heapIndexMap.put(nodes[index2], index1);
// 再交换在堆中的位置
Node tmp = nodes[index1];
nodes[index1] = nodes[index2];
nodes[index2] = tmp;
}
}
// 对堆进行改进后的算法
public static HashMap<Node, Integer> dijkstra2(Node head, int size) {
// size:一共多少个点
NodeHeap nodeHeap = new NodeHeap(size);
// head到节点没有记录,则创造新记录
// 如果有记录,则更新distance,如果值比原值要大,则不更新
nodeHeap.addOrUpdateOrIgnore(head, 0);
HashMap<Node, Integer> result = new HashMap<>();
while (!nodeHeap.isEmpty()) {
// 弹出最小值的点以及它的值
NodeRecord record = nodeHeap.pop();
Node cur = record.node;
int distance = record.distance;
// 遍历更新最小值的点延伸出去的边,更新其他点的路径
for (Edge edge : cur.edges) {
nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);
}
// 把不再更新的达到最小值路径的点保存
result.put(cur, distance);
}
return result;
}
基础第八课题目二:汉诺塔问题
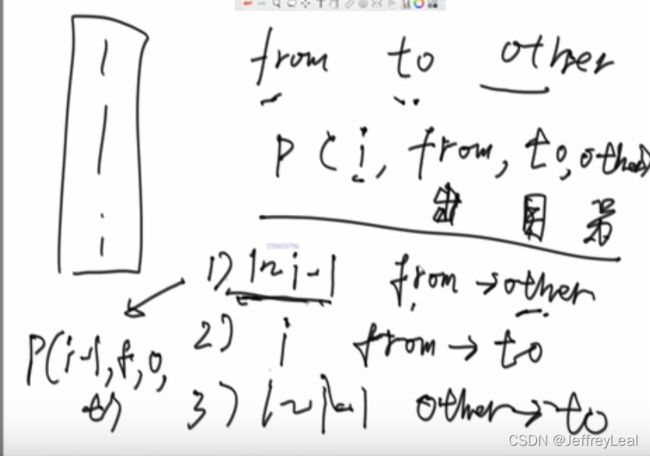
// rest:移动多少个
// down:底部数值是多少
// from:从哪里
// to:移动到哪里
// other:辅助位置
public static void func(int rest, int down, String from, String help, String to) {
if (rest == 1) {
//移动的堆大小为1,底部为down,即移动一个单独的圆盘
System.out.println("move " + down + " from " + from + " to " + to);
} else {
//移动的堆大小为rest-1,底部为down-1,从from移动到help
func(rest - 1, down - 1, from, to, help);
//移动的堆大小为1,底部为down,从from移动到to
func(1, down, from, help, to);
//移动的堆大小为rest-1,底部为down-1,从help移动到to
func(rest - 1, down - 1, help, from, to);
}
}
基础第八课题目三:打印子集
public static void printAllSubsquence(String str) {
char[] chs = str.toCharArray();
process(chs, 0);
}
public static void process(char[] chs, int i) {
if (i == chs.length) {
System.out.println(String.valueOf(chs));
return;
}
// 第i位上的字符打印
process(chs, i + 1);
// 第i位上的字符不打印
char tmp = chs[i];
chs[i] = 0;
process(chs, i + 1);
chs[i] = tmp;
}
public static void function(String str) {
char[] chs = str.toCharArray();
process(chs, 0, new ArrayList<Character>());
}
// res:记录所有结果
public static void process(char[] chs, int i, List<Character> res) {
if(i == chs.length) {
printList(res);
}
List<Character> resKeep = copyList(res);
resKeep.add(chs[i]);
process(chs, i+1, resKeep);
List<Character> resNoInclude = copyList(res);
process(chs, i+1, resNoInclude);
}
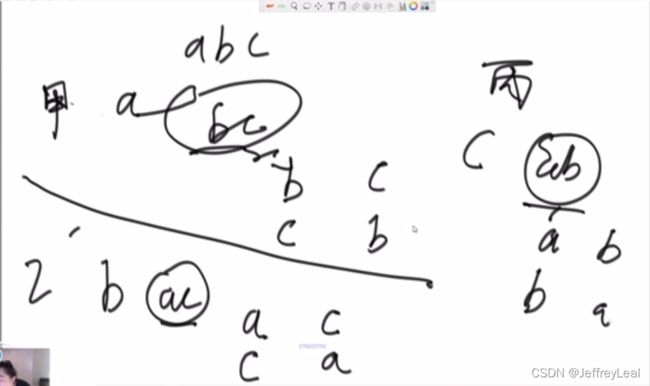
基础第八课题目四:打印字符串全部排列
public static void process(char[] chs, int i, ArrayList<String> res) {
if (i == chs.length) {
// 把所有结果记录到res中
res.add(String.valueOf(chs));
}
// 用来记录这个字符有没有试过,为了去掉重复的
// 例如aaabb,交换0位置和0位置时,会记录
boolean[] visit = new boolean[26];
for (int j = i; j < chs.length; j++) {
if (!visit[chs[j] - 'a']) {
visit[chs[j] - 'a'] = true;
swap(chs, i, j);
process(chs, i + 1, res);
swap(chs, i, j);
}
}
}
基础第八课题目八:2玩家左右抽牌
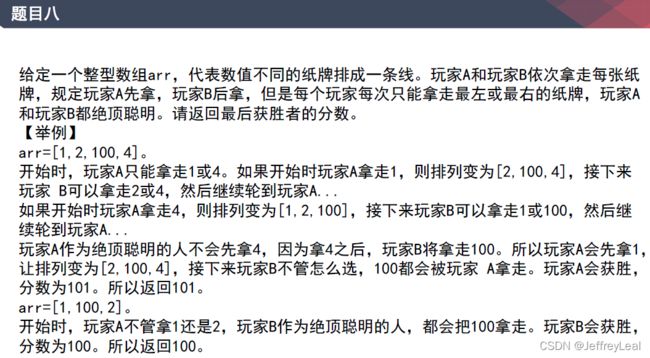
先手函数的返回值,为先手玩家获得的分数:

后手函数的返回值,为先手玩家在后手玩家拿牌后获得的分数:

// 先手玩家获得的分数
public static int win1(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
}
// 先手函数,为先手玩家在拿牌时获得的分数
public static int f(int[] arr, int i, int j) {
if (i == j) {
return arr[i];
}
return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
}
// 后手函数,为先手玩家在后手拿牌后可获得的分数
public static int s(int[] arr, int i, int j) {
if (i == j) {
return 0;
}
return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));
}
基础第八课题目五:逆序栈
// 逆序
public static void reverse(Stack<Integer> stack) {
if (stack.isEmpty()) {
return;
}
// 弹出底部元素并获取
int i = getAndRemoveLastElement(stack);
// 剩余元素逆序
reverse(stack);
// 底部元素放到顶部
stack.push(i);
}
// 栈的结构:栈顶最小,栈底最大
// 将栈底元素弹出
public static int getAndRemoveLastElement(Stack<Integer> stack) {
// 每次递归都弹出顶部元素
int result = stack.pop();
if (stack.isEmpty()) {
return result;
} else {
int last = getAndRemoveLastElement(stack);
// 每次递归都将弹出的顶部元素重新放回去
stack.push(result);
// 每次返回同一个底部元素
return last;
}
}
基础第八课题目六:数组转字符
public static int process(char[] chs, int i) {
if (i == chs.length) {
return 1;// 之前做的决定是有效的,返回1种
}
if (chs[i] == '0') {
return 0;// 10,20已经包含在下面2种判断了
}
if (chs[i] == '1') {
int res = process(chs, i + 1);
if (i + 1 < chs.length) {
res += process(chs, i + 2);
}
return res;
}
if (chs[i] == '2') {
int res = process(chs, i + 1);
if (i + 1 < chs.length && (chs[i + 1] >= '0' && chs[i + 1] <= '6')) {
res += process(chs, i + 2);
}
return res;
}
// 以上代码都不满足,才会执行这行,也就是去到数组末端
return process(chs, i + 1);
}
基础第八课题目七:装载最大价值
public static int maxValue1(int[] weights, int[] values, int bag) {
return process1(weights, values, 0, 0, bag);
}
// 此算法有问题
public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) {
if (alreadyweight > bag) {
return 0;
}
if (i == weights.length) {
return 0;
}
return Math.max(
process1(weights, values, i + 1, alreadyweight, bag),
values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
}
public static int process2(int[] weights, int[] values, int i,
int alreadyweight, int alreadyValue, int bag) {
if (alreadyweight > bag) {
return 0;
}
if (i == weights.length) {
return alreadyValue;
}
return Math.max(
process2(weights, values, i + 1, alreadyweight,
alreadyValue, bag),
process2(weights, values, i + 1,
alreadyweight + weights[i],
alreadyValue + values[i], bag));
}