SVM支持向量机算法

概述

支持向量机(Support Vecor Machine, SVM)本身是一个二元分类算法，是对感知器算法模型的一种扩展，现在的SVM算法支持线性分类和非线性分类的分类应用，并且也能够直接将SVM应用于回归应用中 。我们也可以将SVM应用在多元分类领域中。

概念

• 线性可分(Linearly Separable)：在数据集中，如果可以找出一个超平面，将两组数据分开，那么这个数据集叫做线性可分数据。
• 线性不可分(Linear Inseparable)：在数据集中，没法找出一个超平面，能够将两组数据分开，那么这个数据集就叫做线性不可分数据。
• 分割超平面(Separating Hyperplane)：将数据集分割开来的直线/平面叫做分割超平面。
• 间隔(Margin)：数据点到分割超平面的距离称为间隔。
• 支持向量(Support Vector)：离分割超平面最近的那些点叫做支持向量

数学知识

梯度下降

• 梯度下降法(Gradient Descent， GD)常用于求解无约束情况下凸函数(Convex Function)的极小值，是一种迭代类型的算法，因为凸函数只有一个极值点，故求解出来的极小值点就是函数的最小值点。
• 最优化问题一般是指对于某一个函数而言，求解在其指定作用域上的全局最小值问题，一般分为以下三种情况(备注：以下几种方式求出来的解都有可能是局部极小值，只有当函数是凸函数的时候，才可以得到全局最小值) ：
  • 无约束问题：求解方式一般求解方式梯度下降法
  • 等式约束条件：求解方式一般为拉格朗日乘子法
  • 不等式约束条件：求解方式一般为KKT条件

拉格朗日乘数法

拉格朗日乘子法就是当我们的优化函数存在等值约束的情况下的一种最优化求解方式；其中参数α被称为拉格朗日乘子，要求α不等于0。

对偶问题

在优化问题中，目标函数f(x)存在多种形式，如果目标函数和约束条件都为变量x的线性函数，则称问题为线性规划；如果目标函数为二次函数，则称最优化问题为二次规划；如果目标函数或者约束条件为非线性函数，则称最优化问题为非线性优化。每个线性规划问题都有一个对应的对偶问题。

对偶问题具有以下几个特性：

1. 对偶问题的对偶是原问题；
2. 无论原始问题是否是凸的，对偶问题都是凸优化问题；
3. 对偶问题可以给出原始问题的一个下界；
4. 当满足一定条件的时候，原始问题和对偶问题的解是完美等价的

KKT条件

• KKT条件是泛拉格朗日乘子法的一种形式；主要应用在当我们的优化函数存在不等值约束的情况下的一种最优化求解方式；KKT条件即满足不等式约束情况下的条件
  $$\begin{gathered} \underset{x}{\min }f(x) \\ \text{ s.t }:h_k(x)=0,k=1,2,\dots ,p \\ {g}_j(x)\le 0,j=1,2,\dots ,q \\ L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^p{\alpha }_i{h}_i(x)+\sum _{i=1}^q{\beta }_i{g}_i(x);{\alpha }_i\ne 0,{\beta }_i\ge 0 \\ \underset{x}{\min }L(x,\alpha ,\beta ) \end{gathered}$$

• 可行解必须在约束区域g(x)之内，由图可知可行解x只能在g(x)<0和g(x)=0的区域取得.

  • 当可行解x在g(x)<0的区域中的时候，此时直接极小化f(x)即可得到
  • 当可行解x在g(x)=0的区域中的时候，此时直接等价于等式约束问题的求解
    

• 当可行解在约束内部区域的时候，令β=0即可消去约束

  • 对于参数β的取值而言，在等值约束中，约束函数和目标函数的梯度只要满足平行即可，而在不等式约束中，若β≠0，则说明可行解在约束区域的边界上，这个时候可行解应该尽可能的靠近无约束情况下的解，所以在约束边界上，目标函数的负梯度方向应该远约束区域朝无约束区域时的解，此时约束函数的梯度方向与目标函数的负梯度方向应相同；从而可以得出β>0
    
    $$\begin{gathered} \underset{x}{\min }f(x) \\ \text{ s.t }:g_j(x)\le 0,j=1,2,\dots ,q \\ L(x,\beta )=f(x)+\sum _{i=1}^q{\beta }_i{g}_i(x);{\beta }_i\ge 0 \end{gathered}$$
    $$\begin{array}{l}\begin{array}{l}{\beta }_i\ge 0\\ g_i(x)\le 0\end{array}\}\Rightarrow {\beta }_i{g}_i(x)\le 0\\ \therefore f(x)={\max }_{\beta }L(x,\beta )\\ \therefore {\min }_{x}f(x)={\min }_x{\max }_{\beta }L(x,\beta )\end{array}$$
    $$\begin{array}{l}{\max }_{\beta }{\min }_{x}L(x,\beta )={\max }_{\beta }\left[{\min }_{x}f(x)+{\min }_x\beta g(x)\right]\\ ={\max }_{\beta }{\min }_{x}f(x)+{\max }_{\beta }{\min }_x\beta g(x)={\min }_{x}f(x)+{\max }_{\beta }{\min }_x\beta g(x)\\ \because \begin{array}{l}{\beta }_i\ge 0\\ g_i(x)\le 0\end{array}\}\Rightarrow {\min }_x{\beta }_i{g}_i(x)=\{\begin{array}{l}0,\beta \text{ 为0或者 }g(x)\text{ 为 }0\\ -\infty ,\beta >0\text{ 且 }g(x)<0\end{array}\\ \therefore {\max }_{\beta }{\min }_x{\beta }_i{g}_i(x)=0\\ \therefore {\min }_{x}f(x)={\max }_{\beta }{\min }_{x}L(x,\beta );\beta =0\text{ 或者 }g(x)=0\end{array}$$
    

硬间隔SVM

目标函数推导

考虑二分类问题，y的值为+1、-1

• 设置分隔超平面：$y(x)=w^T\Phi (x)+b$
• 可以得到
  $$\{\begin{array}{l}y\left(x_i\right)>0\iff y_i=+1\\ y\left(x_i\right)<0\iff y_i=-1\end{array}\Rightarrow y_i\cdot y\left(x_i\right)>0$$
• SVM使用距离进行切分的，并进行缩放可得到
  $$dist=\frac{|A{x}_0+B{y}_0+C|}{\sqrt{(}{A}^2+B^2)}\Rightarrow dist=\frac{|f(X_0)|}{||\theta |{|}_2}\Rightarrow \frac{y_i\cdot y(x_i)}{||w||}=\frac{y_i\cdot (w^T\Phi (x_i)+b)}{||w||}$$
• 目的：找到距离分割超平面最近的样本，让它与超平面距离最远
  $$argma{x}_{w,b}mi{n}_i\frac{y_i\cdot (w^T\Phi (x_i)+b}{||w||}\Rightarrow argma{x}_{w,b}\{\frac{1}{||w||}mi{n}_i\left[y_i\cdot (w^T\Phi (x_i)+b)\right]\}$$
• 可以通过等比缩放的方法w的方法，使得正负类别点的函数值都满足$|y|\ge 1$，即$y_i\cdot (w^T\Phi (x_i)+b)\ge 1$，那么
  $$argma{x}_{w,b}\{\frac{1}{||w||}mi{n}_i\left[y_i\cdot (w^T\Phi (x_i)+b)\right]\}\Rightarrow argma{x}_{w,b}\frac{1}{||w||}$$
• 而以上形式不方便求最大值，所以我们将求最大的目标函数修改为求最小的目标函数，为：
  $$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2 \\ \text{ s.t. }{y}_i\left(w^T\cdot \Phi \left(x_i\right)+b\right)\ge 1,i=1,2,\cdots ,n \end{gathered}$$
• 根据拉格朗日乘数法：
  $$L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^n{\alpha }_i{y}_i\left(w^T\cdot \Phi \left(x_i\right)+b)-1\right)$$
• 对原问题进行对偶转换
  $$mi{n}_{w,b}ma{x}_{\alpha }L(w,b,\alpha )\Rightarrow ma{x}_{\alpha }mi{n}_{w,b}L(w,b,\alpha )$$
• 拉格朗日函数对w,b求偏导，并等于0，得：
  $$\begin{gathered} \frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^n{\alpha }_i{y}_i\Phi (x_i) \\ \frac{\partial L}{\partial b}=0\Rightarrow 0=\sum _{i=1}^n{\alpha }_i{y}_i \end{gathered}$$
• 代入
  $$\begin{array}{rl}L(w,b,\alpha )=& \frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^n{\alpha }_i\left(y_i\left(w^T\cdot \Phi \left(x_i\right)+b\right)-1\right)\\ =& \frac{1}{2}{w}^{T}w-w^T\sum _{i=1}^n{\alpha }_i{y}_i\Phi \left(x_i\right)-b\sum _{i=1}^n{\alpha }_i{y}_i+\sum _{i=1}^n{\alpha }_i\\ =& \frac{1}{2}{w}^T\sum _{i=1}^n{\alpha }_i{y}_i\Phi \left(x_i\right)-w^T\sum _{i=1}^n{\alpha }_i{y}_i\Phi \left(x_i\right)-b\cdot 0+\sum _{i=1}^n{\alpha }_i\\ =& \sum _{i=1}^n{\alpha }_i-\frac{1}{2}{\left(\sum _{i=1}^n{\alpha }_i{y}_i\Phi \left(x_i\right)\right)}^T\sum _{i=1}^n{\alpha }_i{y}_i\Phi \left(x_i\right)\\ =& \sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\Phi }^T\left(x_i\right)\Phi \left(x_j\right)\\ a^{\ast }=& \underset{\alpha }{\mathrm{argmax}}\left(\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\Phi }^T\left(x_i\right)\Phi \left(x_j\right)\right)]\end{array}$$
• 对$\alpha$求极大值，添加负号，改为求最小值
  $$\begin{gathered} \underset{\alpha }{\min }-\left(\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\Phi }^T\left(x_i\right)\Phi \left(x_j\right)\right)] \\ \text{ s.t. }{\alpha }_i,i=1,2,\cdots ,n \\ \sum _{i=1}^n{\alpha }_i{y}_i=0 \end{gathered}$$
• 对此等值约束问题求出$\alpha$的最优解
• 通过以上步骤，计算
  $$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\Phi \left(x_i\right)\\ b^{\ast }& =y_i-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(\Phi \left(x_i\right)\cdot \Phi \left(x_j\right)\right)\end{array}$$
• 求得分离超平面：$w^{\ast }\Phi (x)+b^{\ast }=0$
• 则分类函数为：$f(x)=sign(w^{\ast }\Phi (x)+b^{\ast })$

总结

• 要求数据必须是线性可分的；
• 纯线性可分的SVM模型对于异常数据的预测可能会不太准；
• 对于线性可分的数据，SVM分类器的效果非常不错。

软间隔SVM

• 原因：有时候不能满足所有训练集样本点分类正确，这样会降低泛化能力。

如果数据线性不可分，加上松弛因子$\xi \ge 0$，让函数加上松弛因子大于等于1，修改后的约束条件变为：
$$y_i(w\cdot x_i+b)\ge 1-{\xi }_i$$
目标函数修改为：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i \\ \underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i \\ \text{ s.t. }{y}_i\left(w\cdot x_i+b\right)\ge 1-{\xi }_i,i=1,2,\cdots ,n \\ {\xi }_i\ge 0,i=1,2,\cdots ,n \end{gathered}$$
拉格朗日函数为：
$$L(w,b,\xi ,\alpha ,\mu )\equiv \frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^n{\xi }_i-\sum _{i=1}^n{\alpha }_i\left(y_i\left(w\cdot x_i+b\right)-1+{\xi }_i\right)-\sum _{i=1}^n{\mu }_i{\xi }_i$$
对参数求偏导得：
$$\begin{gathered} \frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^n{\alpha }_i{y}_i\varphi \left(x_n\right) \\ \frac{\partial L}{\partial b}=0\Rightarrow 0=\sum _{i=1}^n{\alpha }_i{y}_i \\ \frac{\partial L}{\partial \xi }=0\Rightarrow C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
代入L中，得：
$$mi{n}_{w,b\xi }L(w,b,\xi ,\alpha ,\mu )=-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^n{\alpha }_i$$
求$\alpha$极大值转化为：
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^n{\alpha }_i \\ \text{ s.t. }\sum _{i=1}^n{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C,i=1,2,\dots ,n \end{gathered}$$
对等值约束求最优解$\alpha$

核函数

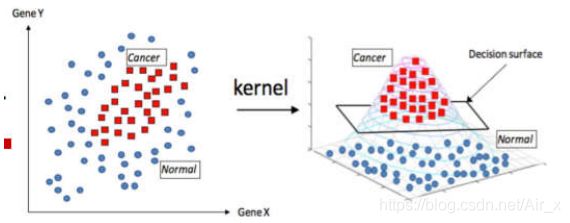
• 可以使用核函数，将原有的空间映射到更高维的空间，从而可以将线性不可分问题处理到在核空间中可分的状态

1. 多项式核函数：$K(x_1,x_2)=(\alpha ||x_q-x_2|{|}^a+r{)}^b,\alpha ,a,b,r为常数$
2. 高斯核函数RBF：$K(x_1,x_2)=e^{-\frac{||x_1-x_2|{|}^2}{2{\sigma }^2}}$
3. Sigmoid核函数：$K(x_1,x_2)=tanh(\gamma \cdot ||x_1-x_2|{|}^a+r),\gamma ,a,r为常数$

• 正常情况下需要使用网格搜索进行处理得到最优的核函数
  

python实现

API

• 分类
  • sklearn.svm.SVC(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’, coef0=0.0, shrinking=True,probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1,decision_function_shape=None,random_state=None)
  • C：C-SVC的惩罚参数C?默认值是1.0 C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的
    惩罚增大
  • kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’,‘sigmoid’, ‘precomputed’
    • RBF函数：高斯核函数
    • sigmoid：sigmoid函数
  • degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略
• 回归
  • 与分类类似
  • sklearn.svm.SVR（kernel =‘rbf’，degree = 3，gamma =‘auto_deprecated’，coef0 = 0.0，tol =0.001，C = 1.0，epsilon = 0.1，shrinking = True，cache_size = 200，verbose = False，max_iter= -1 ）

例子

分类

import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.svm import SVC # SVM分类包
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib as mpl
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

data = pd.read_csv(r'..\datas\iris.txt', header=None)
x = data.iloc[:, :2]
y = data.iloc[:, -1:]
label = LabelEncoder()
y = label.fit_transform(y)

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
# 惩罚项系数， 高斯核函数进行处理   gamma=20
clf = SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')
clf.fit(x_train, y_train.ravel())
y_train_hat = clf.predict(x_train)
print(accuracy_score(y_train, y_train_hat))
y_test_hat = clf.predict(x_test)
print(accuracy_score(y_test, y_test_hat))

iris_feature = '花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'
x1_min, x1_max = x.iloc[:, 0].min(), x.iloc[:, 0].max()  # 第0列的范围
x2_min, x2_max = x.iloc[:, 1].min(), x.iloc[:, 1].max()  # 第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:500j, x2_min:x2_max:500j]  # 生成网格采样点
grid_test = np.stack((x1.flat, x2.flat), axis=1)  # 测试点
Z = clf.decision_function(grid_test)  # 样本到决策面的距离
print(Z)
grid_hat = clf.predict(grid_test)  # 预测分类值
print(grid_hat)
#可视化
grid_hat = grid_hat.reshape(x1.shape)  # 使之与输入的形状相同
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
x1_min, x1_max = x.iloc[:, 0].min(), x.iloc[:, 0].max()  # 第0列的范围
x2_min, x2_max = x.iloc[:, 1].min(), x.iloc[:, 1].max()  # 第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:500j, x2_min:x2_max:500j]  # 生成网格采样点
grid_test = np.stack((x1.flat, x2.flat), axis=1)  # 测试点
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)

plt.scatter(x.iloc[:, 0], x.iloc[:, 1], c=y, edgecolors='k', s=50, cmap=cm_dark)  # 样本
plt.scatter(x_test.iloc[:, 0], x_test.iloc[:, 1], s=120, facecolors='none', zorder=10)  # 圈中测试集样本
plt.xlabel(iris_feature[0], fontsize=13)
plt.ylabel(iris_feature[1], fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u'鸢尾花SVM二特征分类', fontsize=15)
plt.grid()
plt.show()

回归

import numpy as np
from sklearn.svm import SVR # svm做回归的包
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

N = 50
np.random.seed(0)
#进行排序处理， 为了后期画图
x = np.sort(np.random.uniform(0, 6, N), axis=0)
y = 2*np.sin(x) + 0.1*np.random.randn(N)# 加噪声
x = x.reshape(-1, 1)

#高斯核svm回归
svr_rbf = SVR(kernel='rbf', gamma=0.2, C=100)
svr_rbf.fit(x, y)
#线性核svm回归
svr_linear = SVR(kernel='linear', C=100)
svr_linear.fit(x, y)
#多项式核svm回归  提升维度3
svr_poly = SVR(kernel='poly', degree=3, C=100)
svr_poly.fit(x, y)
x_test = np.linspace(x.min(), 1.2*x.max(), 100).reshape(-1, 1)
y_rbf = svr_rbf.predict(x_test)
y_linear = svr_linear.predict(x_test)
y_poly = svr_poly.predict(x_test)
#可视化
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(9, 8), facecolor='w')
plt.plot(x_test, y_rbf, 'r-', linewidth=2, label='高斯核')
plt.plot(x_test, y_linear, 'g-', linewidth=2, label='线性核')
plt.plot(x_test, y_poly, 'b-', linewidth=2, label='多项式核')
plt.plot(x, y, 'mo', markersize=6)
plt.scatter(x[svr_rbf.support_], y[svr_rbf.support_], s=130, c='r', marker='*', 
            label='高斯核支持向量')
plt.legend(loc='lower left')
plt.title('SVR', fontsize=16)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()