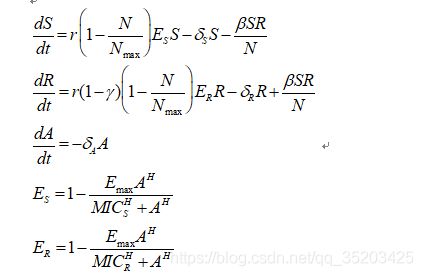Python的Scipy库解微分方程

微分方程：

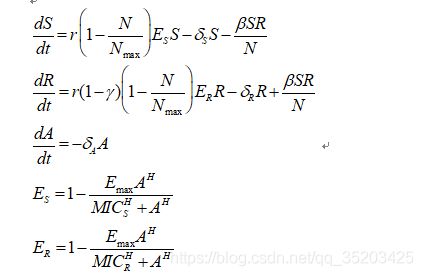
初始值：

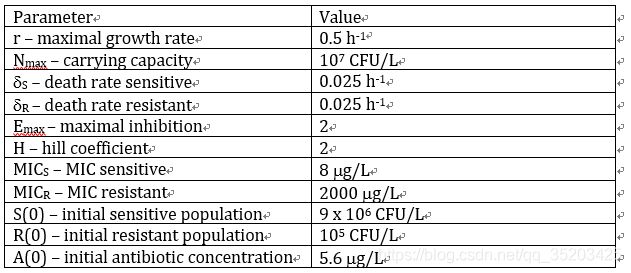
问题：

求解其他三个参数：

代码实现：

import numpy as np
from numpy import zeros, linspace, arange
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def read_data(path):
    with open(path, 'r') as f:
        data = f.read()
    time, num = [], []
    data = data.strip().split('\n')
    for items in data:
        t, n = items.split()
        time.append(float(t))
        num.append(float(n))
    return time, num


# dS/dt
def funcS(S, R, A, r, Nmax, ds, beta, Emax, MICs, H):
    Es = 1 - Emax * np.power(A, H) / (np.power(MICs, H) + np.power(A, H))
    return r * (1 - (R + S) / Nmax) * Es * S - ds * S - beta * S * R / (S + R)


# dR/dt
def funcR(S, R, A, r, Nmax, dr, beta, Emax, MICr, H, gamma):
    Er = 1 - Emax * np.power(A, H) / (np.power(MICr, H) + np.power(A, H))
    return r * (1 - gamma) * (1 - (R + S) / Nmax) * Er * R - dr * R - beta * S * R / (S + R)


# dA/dt
def funcA(A, da):
    return -da * A


# function that need some parameters
def func_all(y, t, parameters):
    S, R, A = y
    r, Nmax, ds, dr, Emax, H, MICs, MICr, beta, gamma, da = parameters
    func1 = funcS(S, R, A, r, Nmax, ds, beta, Emax, MICs, H)
    func2 = funcR(S, R, A, r, Nmax, dr, beta, Emax, MICr, H, gamma)
    func3 = funcA(A, da)
    return np.array([func1, func2, func3])


path = './amrdata.txt'
time, num = read_data(path)
print(time)
print(num)

# set up a parameters
r = 0.5
Nmax = 1.0e7
ds = 0.025
dr = 0.025
Emax = 2
H = 2
MICs = 8
MICr = 2000

# guess
beta = 1.0e-11
gamma = 0.05
da = 0.001

# set up initial conditions
S0 = 9 * 1.0e6
R0 = 1.0e5
A0 = 5.6
y0 = [S0, R0, A0]

# beta_size = 10
# beta_range = []
# for i in range(beta_size):
#     beta_range.append(beta)
#     beta *= 10
# print(beta_range)
bmin, bmax = 1.0e-6, 1.0e-4
gmin, gmax = 0.01, 0.2
amin, amax = 0.001, 0.03

# grid
beta_range = arange(bmin, bmax, (bmax - bmin) / 30)
print(beta_range)
gamma_range = arange(gmin, gmax, (gmax - gmin) / 30)
print(gamma_range)
da_range = arange(amin, amax, (amax - amin) / 30)
print(da_range)

MIN_RMSE = 1000

# find parameters
best_beta = beta
best_gamma = gamma
best_da = da

# grid search
for b in beta_range:
    for g in gamma_range:
        for a in da_range:
            beta = b
            gamma = g
            da = a
            parameters = [r, Nmax, ds, dr, Emax, H, MICs, MICr, beta, gamma, da]
            # Solve the equations using built-in SciPy ODE solver odeint
            sol = odeint(func_all, y0, time, (parameters,))

            S, R, A = sol[:, 0], sol[:, 1], sol[:, 2]  # sensitive bacteria, resistant bacteria and antibiotic
            N = 100 * R / (S + R)  # equal to 100*R/(S + R)

            res = 0
            for i in range(len(num)):
                res += (num[i] - N[i]) ** 2
            RMSE = np.sqrt(res) / len(num)
            # print(RMSE)
            # print("beta= %f, gamma= %f, da= %f" % (beta, gamma, da))
            if RMSE < MIN_RMSE:
                MIN_RMSE = RMSE
                best_beta = beta
                best_gamma = gamma
                best_da = da
                print("---------MIN_RMSE-------\n RMSE= %f" % MIN_RMSE)
                print("beta= %f, gamma= %f, da= %f" % (beta, gamma, da))

parameters = [r, Nmax, ds, dr, Emax, H, MICs, MICr, best_beta, best_gamma, best_da]
sol = odeint(func_all, y0, time, (parameters,))
S, R, A = sol[:, 0], sol[:, 1], sol[:, 2]  # sensitive bacteria, resistant bacteria and antibiotic
N = 100 * R / (S + R)  # equal to 100*R/(S + R)

# fig = plt.figure()
# ax = Axes3D(fig)
# print(sol)
# ax.plot(sol[:, 0], sol[:, 1], sol[:, 2])
# ax.set_xlabel("S concentration ")
# ax.set_ylabel("R concentration ")
# ax.set_zlabel("A concentration ")

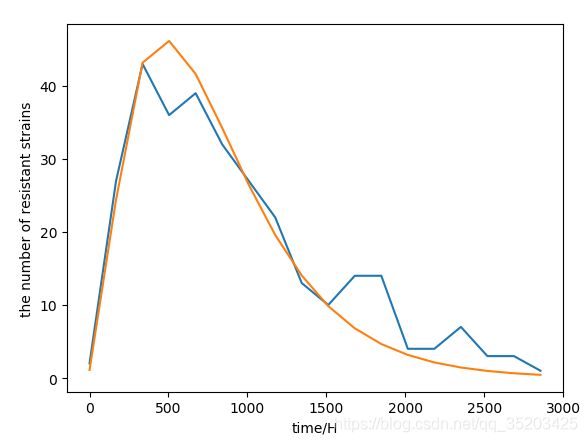
plt.plot(time, num)
plt.plot(time, N)
plt.xlabel("time/H")
plt.ylabel("the number of resistant strains")
plt.show()

拟合情况：

可以看到两条曲线很接近，效果很好。