【ML23】浅谈 Adam Algorithm 解决学习率 α

One step of Gradient Descent

$w_j=w_j-\alpha \frac{d}{dw}J(w,b)$

$b_j=b_j-\alpha \frac{d}{db}J(w,b)$

$J(w,b)=\frac{1}{2m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$

梯度下降 的最终目的是为了能使得预测值最接近实际结果，也就是说，需要 $min(J(w,b))$ 需要将损失函数做到最小，再深入一些，那就是找到损失函数的 global minimum 。

$w=w-\alpha \frac{d}{dw}J(w,b)=w-\alpha \frac{1}{m}\sum _{i=1}^m((f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}$
$b=b-\alpha \frac{d}{db}J(w,b)=w-\alpha \frac{1}{m}\sum _{i=1}^m((f_{w,b}(x^{(i)})-y^{(i)})$

而在 梯度下降 (Gradient Descent) 中，决定每次下降走多少的是 学习率 α (learning rate)。学习率为常数，一般取值 0 - 1 之间，常用为 0.01。

事实证明，学习率的大小不宜大也不宜小，太大容易错过我们的最小值目标，太小能找到最小值但是太慢了。
而为了解决这种问题，学习率的值的设定衍生出一个算法，名称为：Adam Algorithm

相关内容博客：

损失函数： https://blog.csdn.net/weixin_43098506/article/details/127125098
梯度下降： https://blog.csdn.net/weixin_43098506/article/details/127127273
特征缩放： https://blog.csdn.net/weixin_43098506/article/details/127133809
学习率： https://blog.csdn.net/weixin_43098506/article/details/127136108

---

Adam Algorithm

“Adam” : Adaptive Moment estimation 自适应调整 $\alpha$ 学习率大小。

Introduction

下面简单介绍一下 Adam Algorithm，具体内容将在 【DL】即 Deep Learning 的部分划一章详细介绍讲解。

首先 Adam Algorithm 自适应学习率 算法的目的是为了解决值不合适的 学习率 α 导致错过损失函数最小值以及梯度下降过于慢的问题。

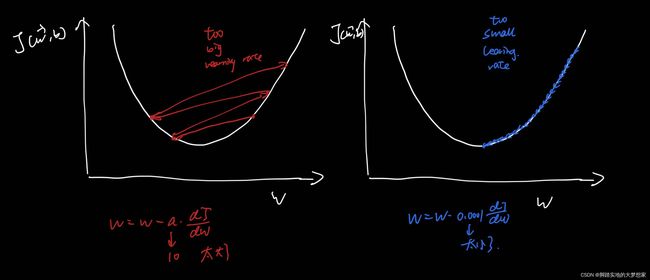
图片来源：吴恩达《Advanced Machine Learning》

如图所示：如果学习率 α 过于小时，Adam 会将其放大，提高效率；如果学习率 α 过于大（右图）时，Adam 会减小学习率 α，使得能最终找到损失函数最小值的点。

假设想要找到一个线性回归函数损失最小的时候参数的值，即：

$f_{(w_1,w_2,...,w_n,b)}(x^{(i)})=w_i{x}_i+b$

那么有：

$w_1=w_1-{\alpha }_1\frac{d}{dw}J(w,b)$

$w_2=w_2-{\alpha }_2\frac{d}{dw}J(w,b)$

$w_3=w_3-{\alpha }_3\frac{d}{dw}J(w,b)$
…
$w_n=w_n-{\alpha }_n\frac{d}{dw}J(w,b)$

与梯度下降不同的是，Adam 对于每一个不同的 $w$ ，有不同的学习率 $\alpha$ 的值。

---

Tensorflow with Adam

在 Tensenflow.teras 中，包含关于 Adam算法 的调用，在深度学习中可以调用其。

假设深度学习模型为：

Code

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense

model = Sequential([
	tf.keras.layers.Dense(units=25, activation='sigmoid', name='layer_1')
	tf.keras.layers.Dense(units=15, activation='sigmoid', name='layer_2')
	tf.keras.layers.Dense(units=10, activation='linear', name='layer_3')
])

model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate = 1e-3),
	loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True))

model.fit(X,Y,epochs=100)

更多关于Adam，会在后期在【DL】中更新！

2022.10.6 国庆节假期，于香港九龙
—>end