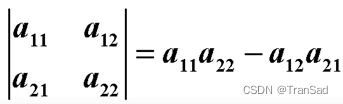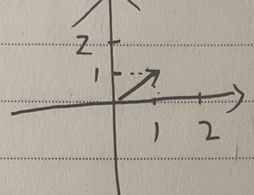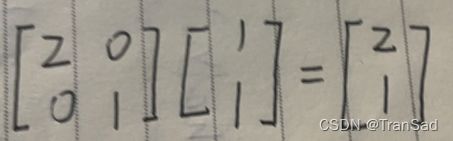矩阵的秩,特征值和特征向量 矩阵基础概念

  矩阵是非常重要而基础的数学知识了。大学课上学线性代数基本就是在学矩阵的各种操作和运算。在深度学习里，几乎所有的参数也都是存放在矩阵中，并通过矩阵来做各种运算。大概把矩阵的基本知识点复习和总结一下。

行列式和矩阵的区别：

行列式和矩阵特别像，行列式长这样（两边是竖线）：

矩阵长这样：

或这样：（两边是个括号）

1.行列式是一个具体的值，他的值表示为：

这是二阶行列式，还有三阶，四阶行列式等，都可以用一套公式结论去求出值。 

行列式我们只说它是“几阶”的，所以行列式的行数和列数是相等的。n阶行列式有n方个元素。

2.矩阵是一堆数值的分布，是一个数值表。矩阵一般有m*n个元素，行数可以和列数不等。

罗列几个我觉得矩阵当中比较重要的小点（一句一条）：

  一般n行1列的矩阵，就是一个列向量；1行n列的矩阵，就是一个行向量；

  如果行列数量一样，则这个矩阵也可以叫做方阵；

  矩阵的主对角线：从左上角到右下角的一条线；

 若主对角线下方全为0，上方不为0，则是上三角矩阵；若主对角线上方全是0，则是下三角矩阵。

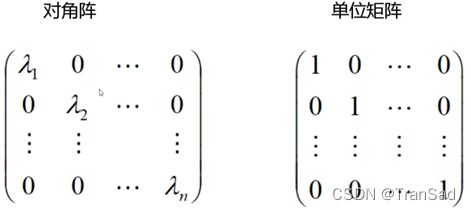
  如果主对角线有值，且其他全是0，则这个矩阵是对角阵。在此基础之上，如果主对角线的值全都是1，则这个矩阵就是单位矩阵。

  矩阵的运算（加法，乘法）之类的就略去了。但特别注意的是矩阵没有交换律（即AB！=BA），但矩阵有结合律 （AB）C=A（BC）和分配律A（B+C）=AB+AC。

  矩阵的转置：行变列，列变行。如果A的转置=A，则A是对称矩阵。

  矩阵求逆：如果AB=BA=1（单位矩阵），则A是B的逆矩阵。AA-1=1。（-1写在右上角）

  向量的内积：a1=(x1,x2,x3),a2=(y1,y2,y3),则向量的内积表示为[a1,a2]=(x1y1,x2y2,x3y3)

矩阵的秩，特征值和特征向量

1.矩阵的秩

  把一个m*n的矩阵拿出来，可以得到它的行向量组（每一行是一个向量，共m个向量）或者列向量组（每一列是一个向量，共n个向量）。

  我们就拿行向量组来分析：

  假如这m个向量，互相全都是线性无关的，则这个矩阵的秩就是m。其实就是：有几个线性无关，则这个矩阵的秩就是几。什么是“线性无关呢”，举个例子，向量[1,2,1]和向量[2,4,2]一看就知道是*2的关系，则这两者“现行有关”；若是向量[1,2,1]和向量[1,5,2],则这两个矩阵线性无关。

  要判断a1,a2,a3是否线性无关，可以令k1a1+k2a2+k3a3=0，通过解方程的方式来判断是否a1，a2，a3线性无关。若k1=k2=k3=0，则线性无关。

  这里有个规律：不管是拿矩阵的行向量组还是列向量组来计算，最终得到的秩都是一样的。

  我的理解：矩阵的秩就是矩阵当中互不相关的向量的个数。

2.矩阵的特征值和特征向量

  首先明确，矩阵乘以向量，可以对向量起到拉伸和旋转的作用。

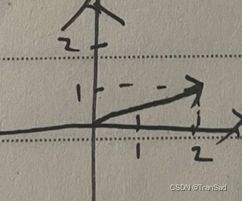
  比如我现在有一个向量（1，1）

  则它现在是这样的：

若拿一个矩阵乘以这个向量（1，1），比如拿这个矩阵来乘：

 可以看出我们会得到结果（2，1），画在图上就是这个效果：

  可以发现这里我们只用了一个对角矩阵，实现了对原向量在横坐标上的一个拉伸。再进一步思考，其实如果矩阵的右上角不为0，或者左下角不为0（假设是个正值），则分别会导致原向量向右旋转或向左旋转。可以得到结论：矩阵可以作用到一个向量，使其旋转或拉伸。

  那有没有一类向量，我使用一个矩阵去作用之后，它的方向不变呢？有！通过这样就可以引出特征值和特征向量来：

  对于一个矩阵A，我们寻找一个非零向量x，使得A作用后的x（即Ax）与x平行，并且大小上满足Ax=λx（λ是个常数）。一旦找到这样的存在，则x就是特征向量，λ就是特征值。

  换个通俗的说法：我们用矩阵A去作用（乘以）世界上所有的向量。其中矩阵A作用后的大部分向量都会被旋转和拉伸，只有矩阵A的特征向量能够独善其身（保持原有的方向）~

  其实，特征向量就代表了矩阵当中的“某一方向”，它能够代表矩阵的关键信息。所以这样两个拥有同样特征的存在相互作用，方向自然不会改变了。而且他们“方向”越一致（越是同道中人~），作用的结果就会越大，λx当中的特征值λ也会越大，因此特征值λ的大小也代表了这个特征向量的重要程度（相比于这一矩阵的其他特征向量）。我记得学习和接触PCA降维的时候，特征值越大的特征向量就越重要，因为这样的向量更能代表图像特征，就是这个意思。

  一个矩阵有多个特征向量，我们用特征空间来表示所有这些。即特征空间包含了所有的特征向量。

  关于矩阵的最常使用的一些概念就整理到此，我最大的感受还是温故而知新，条理清晰了不少。