【深度学习】5 优化算法:mini-batch、Momentum、RMSprop、Adam、学习率衰减
1 引言
历经调试,我们已经建立了一个精确的信息汇总以及决策生成的组织架构,但是光精准还是不够的,要讲究效率。于是我们成立了不同的部门,将公司千千万的员工划归至不同的部门,对于某个时间,各个部门以其专业视角来看待问题。除此之外,还有什么能提高决策生成的效率的方法呢?迭代是一个高度依赖经验的过程,但是也存在一些手段提高迭代的效率。本文内容主要包括两个方面,一是 m i n i − b a t c h mini-batch mini−batch,二是 a d a m adam adam算法。
2 mini-batch
作者本人在深度学习的过程中,由初学时的半知半解,到慢慢深入体会,经历了一个联想的过程,即将抽象的数学表达与现实生活相联系,并将以这一思想贯穿深度学习的写作中。
我们回归至公司情景,设想此时公司有十万人,各自为职,互不相干,公司遇到一个问题,这十万个人唯一对应的这个大老板要求得到一个解决方案。作为公司员工,这个决策生成的方式有哪些呢?
2.1 Batch Gradient Descent
最机械最原始的最单纯的想法,这十万个员工,公说公有理婆说婆有理,最后所有想法艰难汇集成一个方案,然后被老板驳回,反复迭代,可想而知,在时间一定的情况下,迭代的次数会很少,代价最后也会很高,但是这是团体的智慧,集体的意见,能代表所有员工的想法,因此,代价与迭代次数是成反比的,如果做出曲线图,将是非常平滑的。
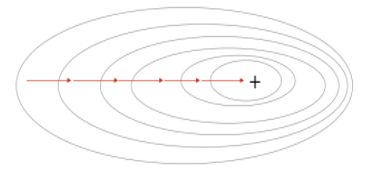
B a t c h G r a d i e n t D e s c e n t Batch Gradient Descent BatchGradientDescent实现的就是这个效果, b a t c h batch batch,英文意思是一批,即将所有的样本打包,统一处理,容易知道,当样本量很小的时候,我们这么做没问题,但是当样本量变得特别大的时候,这对我们电脑的算力提出了非常严峻的挑战,及其影响处理效率。我们先前的实验数据,样本都是百位级别的样子。当面对百万级别的数据时,就得换别的处理方式了。
2.2 mini-batch Gradient Descent
人口扩展到一定规模,就会产生组织,就会形成阶级,这是生物繁衍生产的规律,也是为了提高繁衍生产效率的必然要求。前文所提到的机械原始单纯的处理方式只是一个极端方法,现实生活中我们不会这么做,正如我们所看见的,一个公司由不同部门构成,各个部门包含若干人,一个部门负责相对应的任务,这样可能汇总出来的方案也有所瑕疵,但是效率大大的提升了。

m i n i − b a t c h G r a d i e n t D e s c e n t mini-batch Gradient Descent mini−batchGradientDescent实现的就是这个效果,将样本划归为若干batch,对每个batch依次实行迭代,当所有batch迭代一次后,整体样本就完成了一次迭代,我们称之为one echo。
具体实现方法如下:
1 ) 1) 1)将样本随机重新排列保证随机性;
2 ) 2) 2)设置BatchSize,将样本划分,不能整除的部分作为一个mini-batch
3 ) 3) 3)为神经网络新增一个for循环,用以遍历所有batch实现一次echo。
3 Adam算法
A d a m Adam Adam算法是在 m i n i − b a t c h G r a d i e n t D e s c e n t mini-batch Gradient Descent mini−batchGradientDescent基础上的进一步优化,经过 m i n i − b a t c h G r a d i e n t D e s c e n t mini-batch Gradient Descent mini−batchGradientDescent,我们得到了参数的梯度,在学习率即步长确定的情况下,我们需要通过对梯度的优化进一步解决迭代速度。
3.1 Gradient descent with Momentum
动量梯度下降法,运行速度几乎总是快于标准的梯度下降算法,简而言之,基本的想法就是计算梯度的指数加权平均数,并利用该梯度更新你的权重。
3.1.1 指数加权平均数
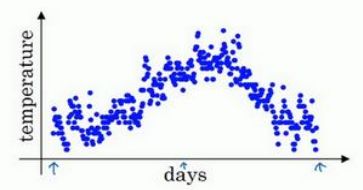
如图为某地一年气温值每日气温设为 θ i \theta_i θi,对应的指数加权平均数设为 v i v_i vi,参数设为 β \beta β。计算步骤如下:
1 ) 1) 1)设 v 0 = 0 v_0=0 v0=0;
2 ) 2) 2) v i = β ∗ v i − 1 + ( 1 − β ) ∗ θ i v_i=\beta*v_{i-1} + (1-\beta)*\theta_i vi=β∗vi−1+(1−β)∗θi;
3 ) 3) 3)(备选)偏差修正,令 v i = v i 1 − β i v_i =\frac{v_i}{1-\beta^i} vi=1−βivi
为 β \beta β设置不同的值,我们得到了如下曲线,其中红线代表 β = 0.9 \beta=0.9 β=0.9,绿线代表 β = 0.98 \beta=0.98 β=0.98,黄线代表 β = 0.5 \beta=0.5 β=0.5。
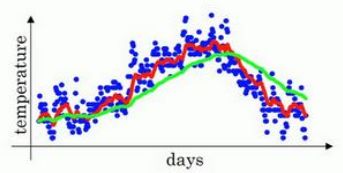
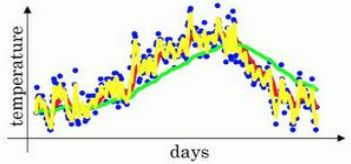
为何会出现这样的曲线呢?我们设 i = 100 i=100 i=100,将上文所述的式子展开可得:
v 100 = β ∗ v 99 + ( 1 − β ) ∗ θ 100 = β ( β ∗ v 98 + ( 1 − β ) ∗ θ 99 ) + ( 1 − β ) ∗ θ 100 v_{100}=\beta*v_{99}+(1-\beta)*\theta_{100}=\beta(\beta*v_{98}+(1-\beta)*\theta_{99})+(1-\beta)*\theta_{100} v100=β∗v99+(1−β)∗θ100=β(β∗v98+(1−β)∗θ99)+(1−β)∗θ100
. . . ... ...
= ( 1 − β ) ∗ θ 100 + β ( 1 − β ) ∗ θ 99 + β ( 1 − β ) 2 ∗ θ 98 + β ( 1 − β ) 3 ∗ θ 97 + . . . β ( 1 − β ) 99 ∗ θ 1 =(1-\beta)*\theta_{100}+\beta(1-\beta)*\theta_{99}+\beta(1-\beta)^2*\theta_{98}+\beta(1-\beta)^3*\theta_{97}+...\beta(1-\beta)^{99}*\theta_{1} =(1−β)∗θ100+β(1−β)∗θ99+β(1−β)2∗θ98+β(1−β)3∗θ97+...β(1−β)99∗θ1
当 β \beta β逐渐变大接近 1 1 1 时,当日温度对于指数加权平均值的影响趋近于0,完全受先前的指数加权平均数的影响;而当 β \beta β逐渐变小接近0时,先前的指数加权平均数的影响趋近于零,其值将完全受制于当日温度,致使曲线噪声增多。我们要做的就是确定好 β \beta β的值,使之能够充分利用历史数据,将先前状态对于当前状态的影响纳入计算,一般设置 β = 0.9 \beta=0.9 β=0.9。
偏差修正如何起作用呢?在最开始,由于初始值设为零,会导致曲线变化较大,将 v i v_i vi除以 1 − β i 1-\beta^i 1−βi后能有效缓解这种情况,且当 i i i增大到一定程度后, 1 − β i 1-\beta^i 1−βi会逐渐趋向1,即越往后,效果会越小。
3.1.2 动量梯度下降法
算法思想为计算梯度的指数加权平均数,并利用该梯度更新你的权重,步骤如下:
1 ) 1) 1)神经网络前向传播以及反向传播完成,得到梯度值计为 d W i , d b i , dW^i,db^i, dWi,dbi,设 V d W 0 = V d b 0 = 0 V_{dW^0}=V_{db^0}=0 VdW0=Vdb0=0;
2 ) 2) 2)利用公式 V d W i = β V d W i − 1 + ( 1 − β ) d W i V_{dW^i}=\beta V_{dW^{i-1}}+(1-\beta)dW^i VdWi=βVdWi−1+(1−β)dWi V d b i = β V d b i − 1 + ( 1 − β ) d b i V_{db^i}=\beta V_{db^{i-1}}+(1-\beta)db^i Vdbi=βVdbi−1+(1−β)dbi计算 V d W i , V d b i V_{dW^i},V_{db^i} VdWi,Vdbi;
3 ) 3) 3)利用公式 W : = W − a ∗ V W i W:=W-a*V_{W^i} W:=W−a∗VWi b : = b − a ∗ V b i b:=b-a*V_{b^i} b:=b−a∗Vbi更新神经网络权重;
3.2 RMSprop
root mean square prop 算法,通过修正梯度下降时的震荡以加快迭代效率。
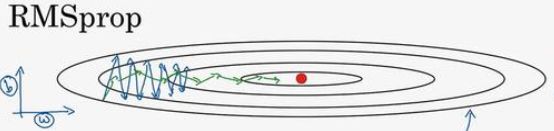
假设未经修正的神经网络迭代路径(即靠近最小代价值的过程)如蓝线所示,这条路径由若干线段组成,这些线段的长度就是学习率,我们通过 R M S p r o p RMSprop RMSprop即可使路径由蓝线变为红线(线段条数变少)。
如何进行优化呢?观察路径线段,我们发现其倾斜程度是最关键的影响因素,我们假设 b b b代表y轴的偏移 W W W代表x轴的偏移,由图可知,此时 b b b很大,我们需要减小 b b b,增大 W W W。 R M S p r o p RMSprop RMSprop算法解决了这个问题,算法步骤如下:
1 ) 1) 1)神经网络前向传播以及反向传播完成,得到梯度值计为 d W i , d b i , dW^i,db^i, dWi,dbi,设 S d W 0 = S d b 0 = 0 S_{dW^0}=S_{db^0}=0 SdW0=Sdb0=0;
2 ) 2) 2)利用公式 S d W i = β S d W i − 1 + ( 1 − β ) d W i S_{dW^i}=\beta S_{dW^{i-1}}+(1-\beta)dW^i SdWi=βSdWi−1+(1−β)dWi S d b i = β S d b i − 1 + ( 1 − β ) d b i S_{db^i}=\beta S_{db^{i-1}}+(1-\beta)db^i Sdbi=βSdbi−1+(1−β)dbi计算 S d W i , S d b i S_{dW^i},S_{db^i} SdWi,Sdbi;
3 ) 3) 3)利用公式 W : = W − a S W i W:=W-\frac{a}{\sqrt {S_{W^i}}} W:=W−SWia b : = b − a S b i b:=b-\frac{a}{\sqrt {S_{b^i}}} b:=b−Sbia更新神经网络权重;
如此使得W的更新变快而b的更新变慢,蓝线变为了红线。
3.3 Adam
A d a m Adam Adam算法将 R M S p r o p RMSprop RMSprop和 M o m e n t u m Momentum Momentum融合实现,步骤如下:
1 ) 1) 1)神经网络前向传播以及反向传播完成,得到梯度值计为 d W i , d b i , dW^i,db^i, dWi,dbi,设 S d W 0 = S d b 0 = 0 S_{dW^0}=S_{db^0}=0 SdW0=Sdb0=0; V d W 0 = V d b 0 = 0 V_{dW^0}=V_{db^0}=0 VdW0=Vdb0=0;
2 ) 2) 2)利用公式 S d W i = β 1 S d W i − 1 + ( 1 − β 1 ) d W i S_{dW^i}=\beta_1 S_{dW^{i-1}}+(1-\beta_1 )dW^i SdWi=β1SdWi−1+(1−β1)dWi S d b i = β 1 S d b i − 1 + ( 1 − β 1 ) d b i S_{db^i}=\beta _1 S_{db^{i-1}}+(1-\beta_1 )db^i Sdbi=β1Sdbi−1+(1−β1)dbi V d W i = β 2 V d W i − 1 + ( 1 − β 2 ) d W i V_{dW^i}=\beta_2 V_{dW^{i-1}}+(1-\beta_2)dW^i VdWi=β2VdWi−1+(1−β2)dWi V d b i = β 2 V d b i − 1 + ( 1 − β 2 ) d b i V_{db^i}=\beta_2 V_{db^{i-1}}+(1-\beta_2)db^i Vdbi=β2Vdbi−1+(1−β2)dbi计算 S d W i , S d b i S_{dW^i},S_{db^i} SdWi,Sdbi V d W i , V d b i V_{dW^i},V_{db^i} VdWi,Vdbi(依据个人情况选择是否加入偏差修正);
3 ) 3) 3)利用公式 W : = W − a V W i S W i W:=W-a\frac{V_{W^i}}{\sqrt {S_{W^i}}} W:=W−aSWiVWi b : = b − a V b i S b i b:=b-a\frac{V_{b^i}}{\sqrt {S_{b^i}}} b:=b−aSbiVbi更新神经网络权重;
算法完成。
b a t c h , m o m e n t u m , a d a m batch,momentum,adam batch,momentum,adam的算法运行结果如下图所示:
M i n i − b a t c h G r a d i e n t d e s c e n t Mini-batch Gradient descent Mini−batchGradientdescent
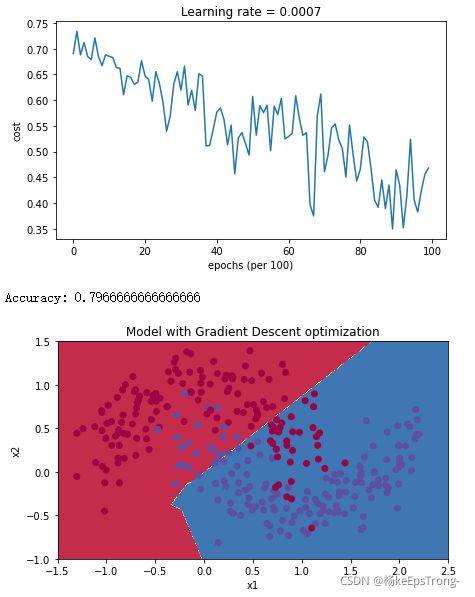
M i n i − b a t c h g r a d i e n t d e s c e n t w i t h m o m e n t u m Mini-batch gradient descent with momentum Mini−batchgradientdescentwithmomentum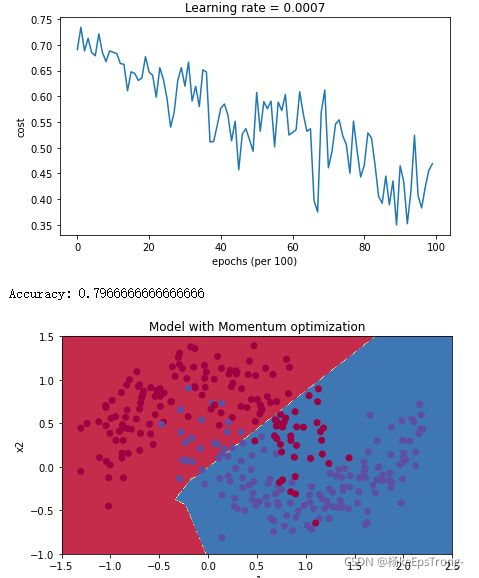
M i n i − b a t c h w i t h A d a m m o d e Mini-batch with Adam mode Mini−batchwithAdammode
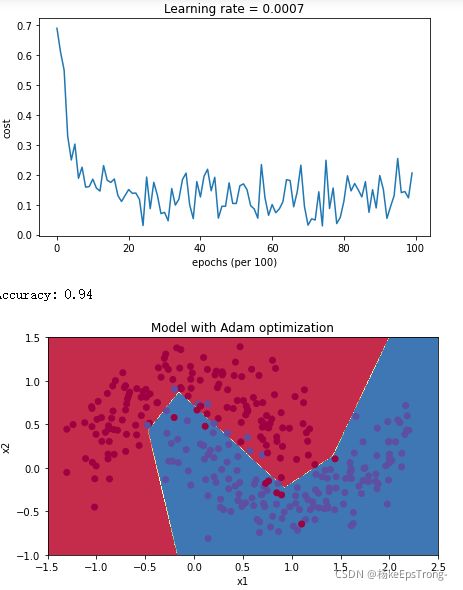
4 学习率衰减
当步长过大,在靠近全局最优解时会出现震荡的情况,即在最优解附近来回摆动,解决办法很简单,即使用学习率衰减公式, a = 1 1 + d e c a y r a t e ∗ e p o c h − n u m a 0 a=\frac{1}{1+decayrate*epoch-num}a_0 a=1+decayrate∗epoch−num1a0此处decayrate为衰减率,是一个超参数,epoch-num即为迭代次数, a 0 a_0 a0为初始学习率。随着迭代次数的增多,公式分母变大,分数变小,乘积变小,学习率变小,实现了学习率随迭代次数衰减的效果。
5 总结
m i n i − b a t c h mini-batch mini−batch解决了样本处理效率问题; A d a m Adam Adam算法解决了权重迭代效率问题;学习率衰减解决了在临近最优解时的摆动问题。