Python BP神经网络解决非线性二分类问题

BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。

我们用BP神经网络来解决非线性的二分类问题

测试样本：

我们运用Python构建BP神经网络，来解决这个非线性分类问题，代码如下

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from math import sqrt


#%% 导入数据
data=pd.read_table('H:/Python/Machine_Learning/BPModel/data.txt',\
                   names=['X','Y','label'])
#%% 样本的分布图
plt.figure('训练样本图')
plt.scatter(data[data['label']==0].loc[:,'X'],\
            data[data['label']==0].loc[:,'Y'],10,label='第一类')
plt.scatter(data[data['label']==1].loc[:,'X'],\
            data[data['label']==1].loc[:,'Y'],10,label='第二类')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('样本分布图')
plt.legend()

#%% BP神经网络模型的训练
def bp_train(feature,label,n_hidden,maxCycle,alpha,n_output):
    '''计算隐含层的输入
    input: feature(mat): 特征
           label(mat): 标签
           n_hidden(int): 隐含层的节点个数
           maxCycle(int):最大的迭代次数
           alpha(float):学习率
           n_output(int):输入层的节点个数
    output: w0(mat):输入层到隐含层之间的权重
            b0(mat):输入层到隐含层之间的偏置
            w1(mat):隐含层到输入层之间的权重
            b1(mat):隐含层到输输出层之间的偏置
    '''
    m,n=np.shape(feature)
    #1 初始化
    w0=np.mat(np.random.rand(n,n_hidden))
    w0=w0*(8.0*sqrt(6)/sqrt(n+n_hidden))-np.mat(np.ones((n,n_hidden)))*\
          (4.0*sqrt(6)/sqrt(n+n_hidden))
    b0=np.mat(np.random.rand(1,n_hidden))
    b0=b0*(8.0*sqrt(6)/sqrt(n+n_hidden))-np.mat(np.ones((1,n_hidden)))*\
          (4.0*sqrt(6)/sqrt(n+n_hidden))
    w1=np.mat(np.random.rand(n_hidden,n_output))
    w1=w1*(8.0*sqrt(6)/sqrt(n_hidden+n_output))-np.mat(np.ones((n_hidden\
          ,n_output)))*(4.0*sqrt(6)/sqrt(n_hidden+n_output))
    b1=np.mat(np.random.rand(1,n_output))
    b1=b1*(8.0*sqrt(6)/sqrt(n_hidden+n_output))-np.mat(np.ones((1,n_output)))*\
          (4.0*sqrt(6)/sqrt(n_hidden+n_output))
          
    #2 训练
    i=0
    while i<=maxCycle:
        #2.1 信号正向传播
        #2.1.1 计算隐含层的输入
        hidden_input=hidden_in(feature,w0,b0) #mXn_hidden
        #2.1.2 计算隐含层的输出
        hidden_output=hidden_out(hidden_input)
        #2.1.3 计算输出层的输入
        output_in=predict_in(hidden_output,w1,b1) #mXn_output
        #2.1.4 计算输出层的输出
        output_out=predict_out(output_in)
        
        #2.2 误差的反向传播
        #2.2.1 隐含层到输出层之间的残差
        delta_output=-np.multiply((label-output_out),partial_sig(output_in))
        #2.2.2 输入层到隐含层之间的残差
        delta_hidden=np.multiply((delta_output*w1.T),partial_sig(hidden_input))
        
        #2.3 修正权重和偏置
        w1=w1-alpha*(hidden_output.T*delta_output)
        b1=b1-alpha*np.sum(delta_output,axis=0)*(1.0/m)
        w0=w0-alpha*(feature.T*delta_hidden)
        b0=b0-alpha*np.sum(delta_hidden,axis=0)*(1.0/m)
        if i%100 ==0:
            print ("\t------- iter:",i,",cost: ",(1.0/2)*get_cost(get_predict\
                    (feature,w0,w1,b0,b1)-label))
        i+=1
    return w0,w1,b0,b1
    
#%% 计算隐含层的输入的hidden_in函数
def hidden_in(feature,w0,b0):
    '''计算隐含层的输入
    input: feature(mat): 特征
           w0(mat): 输入层到隐含层的权重
           b0(mat): 输入层到隐含层的偏置
    output:hidden_in(mat):隐含层的输入
    '''
    m=np.shape(feature)[0]
    hidden_in=feature*w0
    for i in range(m):
        hidden_in[i, ]+=b0
    return hidden_in
        
#%% 计算隐含层的输出的hidden_out函数
def hidden_out(hidden_in):
    '''隐含层的输出
    input:hidden_in(mat):隐含层的输入
    output:hidden_output(mat):隐含层的输出
    '''
    hidden_output=sig(hidden_in)
    return hidden_output

def predict_in(hidden_out,w1,b1):
    '''计算输出层的输入
    input:hidden_out(mat):隐含层的输出
          w1(mat):隐含层到输出层之间的权重
          b1(mat):隐含层到输出层之间的偏置
    output:predict_in(mat):输出层的输入
    '''
    m=np.shape(hidden_out)[0]
    predict_in=hidden_out*w1
    for i in range(m):
        predict_in[i, ]+=b1
    return predict_in

def predict_out(predict_in):
    '''输出层的输出
    input:predict_in(mat):输出层的输入
    output:result(mat):输出层的输出
    '''
    result=sig(predict_in)
    return result

def sig(x):
    '''Sigmoid函数
    input:x(mat/float):自变量，可以使矩阵或是实数
    output:Sigmoid值(mat/float):Sigmoid函数值
    '''
    return 1.0/(1+np.exp(-x))
        
def partial_sig(x):
    '''Sigmoid导函数的值
    input:x(mat/float):自变量，可以是矩阵或者是任意实数
    output:out(mat/float):Sigmoid导函数的值
    '''
    m,n=np.shape(x)
    out=np.mat(np.zeros((m,n)))
    for i in range(m):
        for j in range(n):
            out[i,j]=sig(x[i,j])*(1-sig(x[i,j]))
    return out

def get_cost(cost):
    '''计算当前损失函数的值
    intput: cost(mat):预测值与标签之间的差
    output: cost_sum/m(double):损失函数的值
    '''
    m,n=np.shape(cost)
    
    cost_sum=0.0
    for i in range(m):
        for j in range(n):
            cost_sum += cost[i,j]*cost[i,j]
    return cost_sum/m
        
#%% 对样本进行预测的get_predict函数
def get_predict(feature,w0,w1,b0,b1):
    '''计算最终的预测
    input: feature(mat):特征
           w0(mat):输入层到隐含层之间的权重
           b0(mat):输入层到隐含层之间的偏置
           w1(mat):隐含层到输出层之间的权重
           b1(mat):隐含层到输出层之间的偏置
    output:预测值
    '''
    return predict_out(predict_in(hidden_out(hidden_in(feature,w0,b0)),w1,b1))
    
#%% 训练模型
bpmodel=bp_train(np.mat(data.iloc[:,0:2]),np.mat(data.iloc[:,-1]).T,20,1000,0.1,2)

#%%
pre=np.mat(np.zeros((20000,2)))

for i in range(20000):
    for j in range(2):
        pre[i,j]=np.random.rand()*9-4.5

predict=get_predict(pre,bpmodel[0],bpmodel[1],bpmodel[2],bpmodel[3])   

print(bpmodel[3])
    
#%%
print(predict[:,0])    
train_sample=pd.DataFrame(pre,columns=['X','Y'])    
train_sample['label']=predict[:,0]
#%%
a=train_sample[train_sample['label']>0.5].index
for i in a:
    train_sample.iloc[i,2]=1
b=train_sample[train_sample['label']<=0.5].index
for i in b:
    train_sample.iloc[i,2]=0
            
#%% 预测样本数据图
plt.figure('预测样本')
plt.scatter(train_sample[train_sample['label']==0].loc[:,'X'],\
            train_sample[train_sample['label']==0].loc[:,'Y'],10,label='第一类')
plt.scatter(train_sample[train_sample['label']==1].loc[:,'X'],\
            train_sample[train_sample['label']==1].loc[:,'Y'],10,label='第二类')
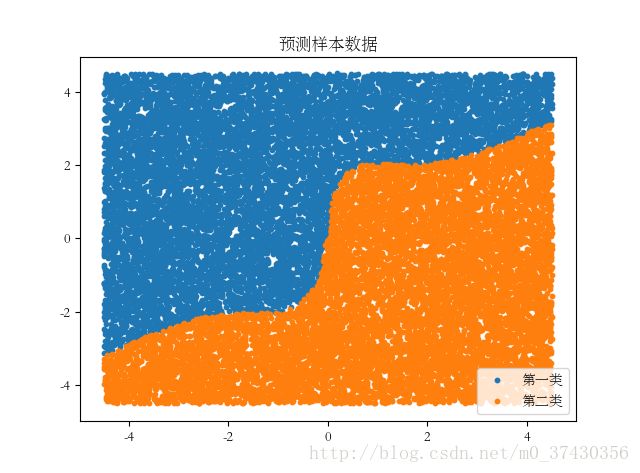
plt.title('预测样本数据')
plt.legend()

最后，我们随机生成20000个样本，并且用训练好的BP模型对这20000个样本进行分类。得到的分类结果如下

分类结果是不是很好呢。顶一个吧！