【论文阅读】Self-Supervised Learning of Graph Neural Networks: A Unified Review

论文题目：Self-Supervised Learning of Graph Neural Networks: A Unified Review
论文地址：https://arxiv.org/abs/2102.10757

1 Introduction

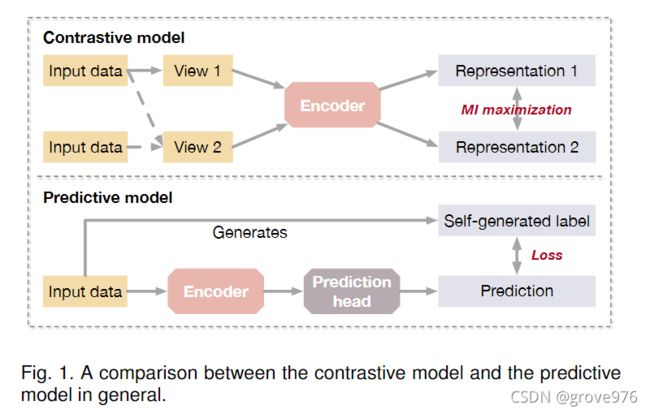
可以将SSL的前置任务分为两类：对比模型和预测模型。

两类的主要区别在于对比模型需要data-data对进行训练，而预测模型需要data-label对，其中label时从数据中自行生成的，如图1

对比模型通常利用自监督来学习数据表示或为下游任务执行预训练。

预测模型是以监督方式训练的，其中标签是基于输入数据的某些属性或通过选择数据的某些部分来生成的

由于图结构数据的独特性，在GNN上应用SSL有几个关键挑战：

• 自监督模型应该从节点属性和图的结构拓扑中捕获基本信息
• 对于对比模型，关键挑战在于如何获得图的良好视图以及不同模型和数据集的图编码器的选择
• 对于预测模型来说，至关重要的是，应该生成什么样的标签，以便学习非琐碎的表示来捕捉节点属性和图结构的信息。

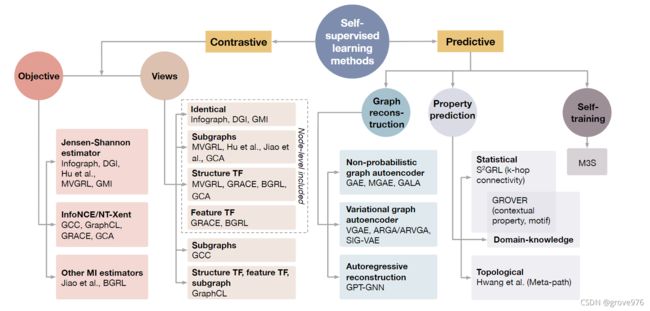
不同类别的自监督学习方法概述如图2

2 Problem Formulation

2.1 Notation

让$\mathcal{P}$表示输入空间$\mathcal{G}$上无标签图的分布。给定一个训练数据集，可以简单地将分布P构造为数据集中样本的均匀分布。自监督可以通过利用来自$\mathcal{P}$的信息并最小化由专门设计的自监督学习任务确定的自监督损失${\mathcal{L}}_{ssl}(f,\mathcal{P})$来促进图编码器 $f$ 的学习

2.2 Paradigms for Self-Supervised Learning

应用自监督的典型训练范式包括无监督表示学习、无监督预训练和辅助学习

unsupervised representation learning

在无监督表示学习中，整个训练过程只有无标签图的分布$\mathcal{P}$可用。给定图数据$(A,X)\sim \mathcal{P}$，则问题表述为：

$$f^{\ast }=arg\underset{f}{\min }{\mathcal{L}}_{ssl}(f,\mathcal{P})$$

此处$f$可以理解为预测出来的数据分布，$f^{\ast }$为图编码器，需要得到一个是预测出来的分布与真实分布差距最小的图编码器

$$H^{\ast }=f^{\ast }(A,X)$$

可以将学习到的表示$H^{\ast }$用在下游任务中

unsupervised pretraining

• 用无标签的图训练图编码器$f$
• 将预训练的编码器$f_{init}$用作有监督微调阶段中编码器的初始化

$$f^{\ast },h^{\ast }=arg\underset{(f,h)}{\min }{\mathcal{L}}_{sup}(f,h,\mathcal{P})$$

with initialization

$$f_{init}=arg\underset{f}{\min }{\mathcal{L}}_{ssl}(f,\mathcal{P})$$

auxiliary learning

我们让$\mathcal{Q}$表示图数据和标签的联合分布，$\mathcal{P}$表示图数据的边缘

我们想要学习解码器$f$和预测$h$，其中$h$是监督下训练$\mathcal{Q}$，$f$在监督和自监督下对$\mathcal{P}$的训练

$$f^{\ast },h^{\ast }=arg\underset{(f,h)}{\min }{\mathcal{L}}_{sup}(f,h,\mathcal{Q})+\lambda {\mathcal{L}}_{ssl}(f,\mathcal{P})$$

3 Contrastive Learning

图对比学习的一个主要区别是：

• 鉴别器的目标是给一个视图表示
• 获取视图的方法
• 计算视图表示的图编码器

3.1 Overview of Contrastive Learning Framework

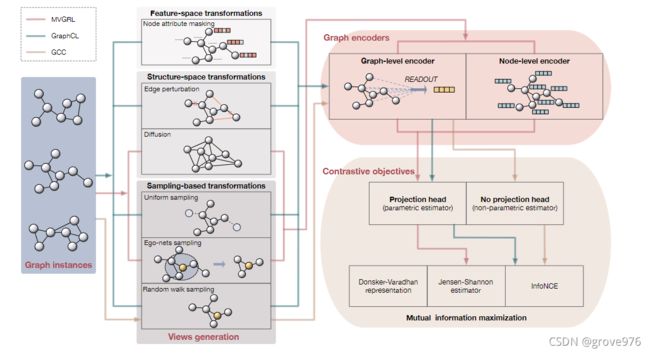
对比学习方法的框架

对于图的编码器，大多数方法采用图级编码器，节点级编码器通常用于节点-图的对比。

给定一个图$(A,X)$，应用多个变换${\mathcal{T}}_1,\cdots ,{\mathcal{T}}_k$得到不同的视图$w_1,\cdots ,w_k$。一组编码网络$f_1,\cdots ,f_k$将相应的输入作为他们的输入，输出为表示$h_1,\cdots ,h_k$

$$w_i={\mathcal{T}}_i(A,X)$$

$$h_i=f_i(w_i),i=1,\cdots ,k$$

对比目标是训练编码器去最大化来自同一个示例图的视图之间的一致性。一致性通常用互信息$\mathcal{I}(h_i,h_j)$，将对比目标形式化为

$$\underset{\{f_i{\}}_{i=1}^k}{\max }\frac{1}{{\sum }_{i\ne j}{\sigma }_{ij}}[\sum _{i\ne j}{\sigma }_{ij}\mathcal{I}(h_i,h_j)]$$

为了有效的计算互信息，通常使用某些估计量作为学习目标

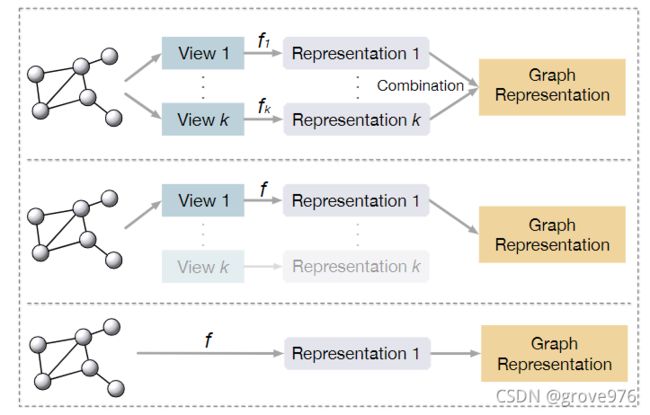
在推理过程中以不同方式使用编码器的三个例子

• 使用多个视图的编码器，并通过组合（如求和或串联）来合并输出表示。
• 在推理过程中仅使用主编码器和相应的视图
• 给定的图直接输入到所有视图共享的唯一编码器以计算其表示

3.2 Contrastive Objectives

3.2.1 Mutual Information Estimation

$\mathcal{I}(x,y)$衡量$x$和$y$的信息共享

$$\begin{array}{rl}\mathcal{I}(x,y)& =D_{KL}(p(x,y)\Vert p(x)p(y))\\ & ={\mathbb{E}}_{p(x,y)}[log\frac{p(x,y)}{p(x)p(y)}]\end{array}$$

• $D_{KL}$：KL散度

3.3 Graph View Generation

分为三种类型：特征变换、结构变换、基于采样的变换

特征变换表示为：

$${\mathcal{T}}_{feat}(A,X)=(A,{\mathcal{T}}_X(X))$$

结构变换表示为：

$${\mathcal{T}}_{struct}(A,X)=({\mathcal{T}}_A(A),X)$$

基于采样的变换表示为：

$${\mathcal{T}}_{sample}(A,X)=(A[S;S],X[S])$$

此处的$S$为节点的子集，采样按行选取

3.3.1 Feature Transformations

Node attribute masking

随机的屏蔽所有节点的一小部分属性，用随机值或常数替代

$${\mathcal{T}}_X^{(mask)}(X)=X\ast (1-1_m)+M\ast 1_m$$

• $M$：带有掩码值的矩阵
• $1_m$：掩码位置指示矩阵

Structure Transformations

两种类型的结构变换：边扰动、扩散

边扰动：随机的添加或删除边

$${\mathcal{T}}_A^{(pert)}(A)=A\ast (1-1_p)+(1-A)\ast 1_p$$

• $1_p$：扰动位置指示矩阵

扩散：在随机游走基础上，在节点之间建立新的连接，目的是生成图形的全局视图$(S,X)$，与局部视图$(A,X)$形成对比

$${\mathcal{T}}_A^{(heat)}(A)=exp(tA{D}^{-1}-t)$$

$${\mathcal{T}}_A^{(PPR)}(A)=\alpha (I_n-(1-\alpha )D^{-1/2}A{D}^{-1/2}{)}^{-1}$$

**基于中心性的边去除：**根据中心性分数确定的预先计算的概率随机删除边缘。

3.3.3 Sampling-Based Transformations

基于采样的变换：uniform sampling、random walk sampling、ego-nets sampling

Uniform sampling

从全部节点中均匀采样一定数量的点以及相关的边构成子图

Ego-nets sampling

采样L阶邻居以及对应的边

$$\begin{gathered} w_i={\mathcal{T}}_i(A,X)=(A[{\mathcal{N}}_L(v_i);{\mathcal{N}}_{\mathcal{L}}(v_i)],X[{\mathcal{N}}_L(v_i)]), \\ {\mathcal{N}}_{\mathcal{L}}(v_i)=\{v:d(v,v_i)\le L\} \end{gathered}$$

Random walk sampling

在 GCC 中提出基于从给定节点开始的随机游走对子图进行采样。

有$p_{ij}$的概率从$v_i$走到$v_j$，有$p_r=0.8$的概率回到起始节点

3.4 Graph Encoders

3.4.1 Node-Level and Graph-Level Representations

获得节点$v$的表示$h_v$的最直接的方法是使用编码器最后一层$K$的节点特征，即$h_v=x_v^{(K)}$

连接所有层的节点特征产生的节点级表示与节点特征具有不同的维度。为了避免向量维度上的这种不一致，连接所有层的节点特征，然后进行线性变换

$$h_v=CONCAT([x_v^{(k)}{]}_{k=1}^K)W$$

为了节点排列不变性，求和和取平均是最常见的$READOUT$函数

$$\begin{array}{rl}{h}_{graph}=READOUT(H)& =\sigma (\sum _{v=1}^{|V|}{h}_v)\\ & =\sigma (\frac{1}{|V|}\sum _{v=1}^{|V|}{h}_v)\end{array}$$

4 Predictive Learning

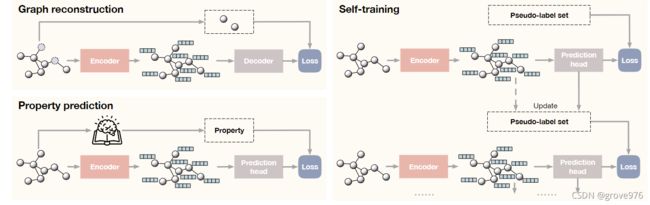
将图的预测学习框架总结为：

• 图重构，学会重建给定图的某些部分
• 图属性预测，学习给定图的non-trivial属性预测
• 带有伪标签的多阶段自训练

4.1 Graph Reconstruction

4.1.1 Non-Probabilistic Graph Autoencoders

GAE： 重建邻接矩阵

计算重建后的邻接矩阵：

$$\begin{gathered} \hat{A}=g(H)=\sigma (H{H}^T) \\ H=f(A,X) \end{gathered}$$

通过$\hat{A}$和$A$之间的交叉熵损失优化。

GraphSAGE： 基于不同的目标（包括负采样）对邻接矩阵进行自监督

superGAT： 将GAE目标作为训练图注意网络期间的自我监督辅助损失，以指导学习更具表现力的注意操作器

MGAE：遵循去噪自编码器的思想。对随机损坏的节点属性进行重建，使用单层自编码器$f_{\theta }$和目标

$$\sum _{i=1}^m\Vert X-f_{\theta }(A,{\tilde{X}}_i){\Vert }^2+\lambda \Vert \theta {\Vert }^2$$

$H_i:=f_{\theta }(A,{\tilde{X}}_i)$被认为是重构的表示

可堆叠多个类似的单层自编码器以达到更好的效果，最后一层得到的表示被用作下游任务

$$\begin{gathered} \sum _{i=1}^m\Vert H^{(l-1)}-H_i^{(l)}{\Vert }^2+\lambda \Vert {\theta }_l{\Vert }^2 \\ {H}_i^{(l)}=f_{{\theta }_l}(A,{\tilde{H}}_i^{(l-1)}) \end{gathered}$$

GALA：引入了具有对称编码器和解码器的多层自动编码器，与 GAE 和 MGAE 不同。

通过执行拉普拉斯锐化来设计解码器，促使每个节点的解码表示与其邻居的质心不同，解码器$g$中的拉普拉斯锐化层计算方式：

$${\hat{X}}^{(l)}=2{\hat{X}}^{(l-1)}-D^{-1}A{X}^{(l-1)}$$

重建特征矩阵通过优化均方误差$\Vert \hat{X}-X{\Vert }^2$

$$\hat{X}=g(A,H),H=f(A,X)$$

Attribute masking：也成为图补全，在图自动编码器框架下通过重构被屏蔽的节点属性来预训练图编码器的策略，给定具有随机屏蔽的节点属性的图，编码器$f$计算节点级表示$H$，将线性投影作为解码器$g$，以重构屏蔽属性

4.1.2 Variational Graph Autoencoders

VGAE： 采用了变分自编码器的思想，用已知的图经过编码（图卷积）学到节点向量表示的分布，在分布中采样得到节点的向量表示，然后进行解码重新构建图。其损失为：

$${\mathbb{E}}_{q(H|A,X)}[logp(A|H)]-KL[q(H|A,X)\Vert p(H)]$$

$$q(H|A,X)=\prod _{i=1}^{|V|}\mathcal{N}(h_i)|{\mu }_i(A,X),{\Sigma }_i(A,X)$$

ARGA/ARVGA：使用对抗网络对自编码器进行正则化，该网络强制潜变量的分布以匹配高斯先验。除了编码器和解码器之外，鉴别器被训练来区分由编码器产生的假数据和从高斯分布采样的真实数据。由于对抗性正则化可证明是潜变量分布和高斯先验之间的JS-散度的等价性，ARGA/ARVGA可获得与VGAE相似的效果，但更强的正则化

SIG-VAE：将变分图自动编码器中的推理模型替换为多个随机层的层次结构，以实现更灵活的潜在变量模型。

4.1.3 Autoregressive Reconstruction

GPT-GNN： 提出了一个自回归框架来对给定的图进行重构。给定一个节点和边随机屏蔽的图，GPT-GNN 一次生成一个屏蔽节点及其边，并优化当前迭代中生成的节点和边的可能性。GPT-GNN 迭代生成节点和边，直到生成所有屏蔽节点。

4.2 Graph Property Prediction

除了重建之外，执行自监督预测学习的一种有效方法是根据图数据中未明确提供的信息图属性来设计预测任务。自监督训练的常用属性包括拓扑属性、统计属性和涉及领域知识的属性。

$S^{2}GRL$：将邻接矩阵概括为两个给定给的节点之间的k-hop连通性预测，动机是两个节点之间的互动并不限于他们的直接连接

给定任何节点对的编码表示，预测头执行分类。$S^{2}GRL$训练编码器和预测头来分类这对节点之间的跳数

Meta-path prediction：为异构图提供自监督。长度为$l$的元路径定义为$(t_1,\cdots ,t_l)$，$t_i$表示路径中第$i$条边的种类。给定异构图中的两个节点和$k$个元路径，编码器$f$和预测头$g_i(i=1,\cdots ,k)$被训练来预测这两个节点是否由各个元路径连接。

GROVER：通过两个预测学习任务对分子图数据执行自监督学习。

在上下文属性预测中，编码器和预测头被训练来预测给定节点（原子）的$k$跳邻居内的“原子-键-计数”关系

图级模体预测任务被应用于涉及领域知识的自我监督，给定一个模体列表，图级预测头预测每个模体的存在，作为一个多标签分类任务

4.3 Multi-Stage Self-Training

预测目标不是从输入图中获得的标签，而是从前一阶段的预测中获得的伪标签。

M3S：应用 DeepCluster 和对齐机制在多阶段自训练的基础上生成伪标签

在每个阶段对节点级表示执行 K 均值聚类，然后从聚类中获得的标签与给定的真实标签对齐。只有在匹配当前阶段分类器的预测时，才将具有聚类伪标签的节点添加到标记集中，用于下一阶段的自训练。与基本的多阶段自训练相比，M3S认为 DeepCluster 和调整机制是一种自我检查机制，因此提供了更强的自监督。

5 Summary of Learning Tasks and Datasets

自监督学习任务分为两种：图级别inductive learning、节点级别transductive learning

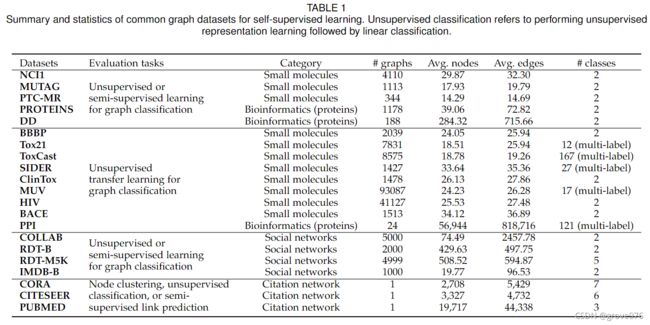
数据集：

5.1 Graph-Level Inductive Learning

在多个数据集上进行

用于图级学习任务的常用数据集可分为三种类型，化学分子数据集、蛋白质数据集和社交网络数据集。

5.2 Node-Level Transductive Learning

7 Conclusion

对于预测性学习，我们根据标签从数据中产生的方式，将现有的方法分为图谱重建、属性预测和自我训练。