论文阅读Targetless Calibration of LiDAR-IMU System Based on Continuous-time Batch Optimization（含代码解读）

原文链接: https://arxiv.org/pdf/2007.14759v1.pdf

代码地址GitHub - APRIL-ZJU/lidar_IMU_calib: Targetless Calibration of LiDAR-IMU System Based on Continuous-time Batch Estimation

摘要：传感器标定时多传感器融合中的基础模块。本文剔除一个精确的LIDAR-IMU标定系统，用于标定3D LIDAR和IMU的6自由度外参。考虑到LIDAR和IMU数据频率较高，LI-Calib采用基于B-Spline的连续时间轨迹方程，对比基于离散时间的方法，这种方法更适用于融合高频和非时间同步系统。LI-Calib将空间分解为一个个cells，然后在数据关联中识别平面元素(planar segments)，这就将标定问题构造成了一个约束良好的问题，其在没有人工标志物的环境中也适用。所提方法在仿真和实际环境数据中均得到验证，结果显示出在一般van环境中的高精度和良好的可重复性。

I  引言

        多传感器融合在机器人领域是一个大的发展方向。LIDAR由于其高精度，鲁棒性和可靠性而被广泛使用，比如定位，语义建图，目标跟踪检测。但是LiDAR的一帧3D点是在不同时刻获得，所以导致运动畸变。为了去畸变，作为高频自我位姿估计的IMU被广泛使用。一般来说，LiDAR-IMU系统对于不同环境更可靠。

        自我位姿评估，定位，建图和导航的精度高度依赖传感器之间标定的精度。手动测量相对旋转和平移精度不够高，也不实用。对于LiDAR-IMu标定问题，需要注意的是在一帧激光scan中的耽搁点是在不同时刻采样得到，其在LiDAR坐标系下的确切位姿与其被接收到时的LiDAR位置相关。对于每个点的位姿估计对于畸变去除都是必要的。基于离散时间的方法在关键帧位姿之间使用插值，其对于高动态场景牺牲了精度。[7]使用高斯过程回国来插值IMU观测，部分解决了第精度IMU和高频LiDAR点的问题。[8]提出的camera-IMU-LiDAR系统，使用基于连续时间批量估计的两阶段方法。camera-IMU系统首先使用chessboard进行标定，然后单线束激光雷达基于camera-IMU系统进行标定。

        受[8]的启发，我们提出了一个精确的LiDAR-IMU标定方法，其使用了连续时间框架，也是我们以前工作的一个拓展[9]。通过使用时间基函数参数化轨迹。此基于连续时间的方法能够获得轨迹上任意时刻的位置，这对于高频观测传感器的标定是很合适的。而且，因为IMU的角速度和加速度测量是时间基函数的微分采样得到，这种连续时间方程和IMU的配合也很自然。总结一下contributions：

        1）提出一种基于连续时间批量优化的高精度和可重复的LiDAR-IMU标定系统，而不需要额外的传感器或者特殊设计的标志物。

        2）提出一种新颖的基于连续时间轨迹的LiDAR-IMU标定问题的方法，IMU原始数据和LiDAR点到面元的距离引入的残差在连续时间批量优化方程里面被最小化。

        3）仿真和实采数据都取得很好效果。并且将系统开源，这也是第一个开源得3D LiDAR-IMU标定工具。

III 轨迹表示方法和下标

        {I}表示IMU系，{L}表示LiDAR系，{M}表示map系，其与标定时的第一帧LiDAR坐标系{L0}一样。表示LiDAR到IMU的变换。

        我们使用B-Spline来参数化轨迹，是因为它提供闭式解析微分，可以简化状态估计时高频观测数据的融合。B-Spline也具有很好的局部可控性，意味着单个控制点的更新只影响样条曲线上的相邻的几个元素。这个性质使用有限的控制点产生稀疏系统。这里有几种方法使用B-Spline来代表刚体运动归uji。[21][22]使用一个样条取线参数化SE(3)上的位姿，另外[23][24]使用两条样条取线来分别表示上的平移旋转。[24]中总结得到，联合形式可能扭矩最小(torque-minimal)，但是很难控制平移曲线的形状，因为平移和旋转是紧耦合的。并且耦合的旋转和平移在我们的标定问题中很难求解，所以我们选择分开表示平移和旋转来参数化轨迹。

        Cox-de Boor递推公式[25]定义了B-Spline的基本方程,[26][27]很方便地使用矩阵方程来表示splines。当B-Spline的结点(knots)均匀分布时，B-Spline可以同步它的度(degree)完全定义。特别的是，对于一个d个度的均匀B-Spline来说，时间段内的平移由对应的控制点控制，对于均匀的B-Spline的矩阵形式可以表示为

                                                

                                             

        速度和加速度为

         kontiki中对应代码为 lidar_IMU_calib/thirdparty/Kontiki/include/kontiki/trajectories/uniform_r3_spline_trajectory.h

Result Evaluate(T t, int flags) const override {
    auto result = std::make_unique>(flags);

    int i0;
    T u;
    this->CalculateIndexAndInterpolationAmount(t, i0, u);
    // std::cout << "t=" << t << " i0=" << i0 << " u=" << u << std::endl;

    const size_t N = this->NumKnots();
    if ((N < 4) || (i0 < 0) || (i0 > (N - 4))) {
      std::stringstream ss;
      ss << "t=" << t << " i0=" << i0 << " is out of range for spline with ncp=" << N;
      throw std::range_error(ss.str());
    }

    Vector4 Up, Uv, Ua; // 插值函数的u矩阵
    Vector4 Bp, Bv, Ba; //u^T*M矩阵，第i个元素代表u^T和M矩阵的第i列相乘的结果
    T u2, u3;
    Vector3 &p = result->position;
    Vector3 &v = result->velocity;
    Vector3 &a = result->acceleration;
    T dt_inv = T(1)/this->dt();

    if (result->needs.Position() || result->needs.Velocity())
      u2 = ceres::pow(u, 2);
    if (flags & EvalPosition)
      u3 = ceres::pow(u, 3);

    if (result->needs.Position()) {
      Up = Vector4(T(1), u, u2, u3); 
      Bp = Up.transpose()*M.cast();
      p.setZero();
    }

    if (result->needs.Velocity()) {
      Uv = dt_inv*Vector4(T(0), T(1), T(2)*u, T(3)*u2); // (u^T)'/t
      Bv = Uv.transpose()*M.cast();
      v.setZero();
    }

    if (result->needs.Acceleration()) {
      Ua = ceres::pow(dt_inv, 2)*Vector4(T(0), T(0), T(2), T(6)*u); // (u^T)''/(t^2)
      Ba = Ua.transpose()*M.cast();
      a.setZero();
    }

    // 4个控制点
    for (int i = i0; i < i0 + 4; ++i) {
      Vector3Map cp = this->ControlPoint(i); // 每个控制点位置

      if (flags & EvalPosition)
        p += Bp(i - i0)*cp; // 对位置加权

      if (flags & EvalVelocity)
        v += Bv(i - i0)*cp; // 对速度加权

      if (flags & EvalAcceleration)
        a += Ba(i - i0)*cp;

    }

    // This trajectory is not concerned with orientations, so just return identity/zero if requested
    if (result->needs.Orientation())
      result->orientation.setIdentity();
    if (result->needs.AngularVelocity())
      result->angular_velocity.setZero();

    return result;
  }

        表示样条的第j列，只依赖与平均B-Spline的度。论文中使用立方B样条,，则                

                                                

        将(1)变形，可得

                                

        则相应的矩阵

                                                

        对(1)(2)(3)(4)的理解：三次B样条曲线拟合算法_残影丶的博客-CSDN博客_b样条曲线拟合

        可以发现矩阵结果与博客的一样 

         同理，累加形式的(3)也经常被用于参数化SO(3)[23,24,27].[28]第一次提出使用单位四元数作为控制点。我们可以发现与(3)的形式非常相像。

        

        SO(3)曲线的角速度获取可以由[27]获取，konkiti中代码为idar_IMU_calib/thirdparty/Kontiki/include/kontiki/trajectories/uniform_so3_spline_trajectory.h

（这个的公式推导看起来有点复杂）

Result Evaluate(T t, int flags) const override {
  auto result = std::make_unique>(flags);

  // 因为SO3曲线无法获取位置，速度，加速度，所以置为0
  if (result->needs.Position())
    result->position.setZero();
  if (result->needs.Velocity())
    result->velocity.setZero();
  if (result->needs.Acceleration())
    result->acceleration.setZero();

  // Early return if we shouldn't calculate rotation components
  if (!result->needs.AnyRotation()) {
    return result;
  }

  // Since angular velocity computations implicitly requires orientation computations
  // we can henceforth assume do_orientation=true

  int i0; // 相距最近的前一个结点
  T u; // 与相距最近的前一个结点的距离
  this->CalculateIndexAndInterpolationAmount(t, i0, u);

  const size_t N = this->NumKnots();
  if ((N < 4) || (i0 < 0) || (i0 > (N - 4))) {
    std::stringstream ss;
    ss << "t=" << t << " i0=" << i0 << " is out of range for spline with ncp=" << N;
    throw std::range_error(ss.str());
  }

  Vector4 U, dU;
  Vector4 B, dB;
  T u2 = ceres::pow(u, 2);
  T u3 = ceres::pow(u, 3);
  T dt_inv = T(1) / this->dt();

  U = Vector4(T(1), u, u2, u3);
  B = U.transpose() * M_cumul.cast();

  if (result->needs.AngularVelocity()) {
    dU = dt_inv * Vector4(T(0), T(1), T(2) * u, T(3) * u2);
    dB = dU.transpose() * M_cumul.cast();
  }

  Quaternion &q = result->orientation;

  // These parts are updated when computing the derivative
  Quaternion dq_parts[3] = {{T(1), T(0), T(0), T(0)},
                            {T(1), T(0), T(0), T(0)},
                            {T(1), T(0), T(0), T(0)}};

  q = this->ControlPoint(i0);
  const int K = (i0 + 4);
  for (int i=(i0 + 1); i < K; ++i) {
    // Orientation
    QuaternionMap qa = this->ControlPoint(i - 1);
    QuaternionMap qb = this->ControlPoint(i);
    Quaternion omega = math::logq(qa.conjugate() * qb);
    Quaternion eomegab = math::expq(Quaternion(omega.coeffs() * B(i-i0)));
    q *= eomegab;

    // Angular velocity
    // This iterative scheme follows from the product rule of derivatives
    if (result->needs.AngularVelocity()) {
      for (int j = (i0 + 1); j < K; ++j) {
        const int m = j - i0 - 1;
        if (i==j) {
          dq_parts[m] *= Quaternion(omega.coeffs()*dB(i-i0));
        }
        dq_parts[m] *= eomegab;
      }
    }
  }

  if (result->needs.AngularVelocity()) {
    Quaternion dq = this->ControlPoint(i0) * Quaternion(dq_parts[0].coeffs() + dq_parts[1].coeffs() + dq_parts[2].coeffs());
    result->angular_velocity = math::angular_velocity(q, dq);
  }

  return result;
}

        在这个标定系统中，我们使用方程(1)(5)参数化连续的6自由度的IMU位姿。样条曲线关于时间的导数很容易求出[27]，则局部IMU坐标系下的线加速度和角速度表示为：

         

        

        上述方程中，和一样。我们将第一帧IMU坐标系作为IMU轨迹的参考系为IMU坐标系下的重力向量。

IV 方法

        整个系统的pipeline在Fig.2中呈现。首先，lidar到IMU系的旋转外参初始化由IMU旋转对齐到LiDAR旋转得到(see IV-A)，其中LiDAR的旋转由基于NDT的里程计获得。初始化完成之后，我们就可以部分去除LiDAR scan中的运动畸变，可以从LiDAR里程计中获得更好的LiDAR位姿估计。LiDAR 面元地图使用LiDAR位姿初始化(see IV-B),点到面元的对应对也是这样。然后，对LiDAR和IMU测量执行基于批量优化的连续时间优化来估计状态量（包含外参）(see IV-C)。最后，有了优化的当前的最优估计，我们更新面元地图，点到平面的数据关联和地带优化估计的状态(see IV-D)。

 A. 旋转外参的初始化

        受[30]的启发，我门通过对齐LiDAR和IMU的旋转序列来初始化旋转外参。已知从IMU传感器获得了一系列角速度测量,我们就可以基于方程(5)来拟合旋转B样条曲线，一系列被拟合B样条曲线的四元数控制点就可以通过求解下列最小二乘问题求解出来：

        

        其中的为时刻IMU测量的角速度。值得注意的是，在优化是固定为单位四元数。在方程(8)中，我们尝试通过原始的IMU数据拟合旋转方程的B样条曲线，而不是IMU积分得到的相对位姿，后者不够精确，且容易受到IMU的噪声和零偏的影响。 

        为了学习一下kontiki的使用，我从源代码中将IMU的轨迹拟合（包含旋转和平移）独立出来一个模块，并使用pangolin进行了可视化，也使用了yaml-cpp，感兴趣的小伙伴可以去看看，代码地址为kontiki_tutorial 。对于lidar观测的加入，我还在持续学习。

     通过使用基于NDT配准的scan2map匹配，我们可以估计出LiDAR scan的位姿。因此，很容易获得连续LiDAR帧之间的相对旋转。同时，在时间段内IMU坐标系下的相对旋转也可以很容易从拟合的B样条曲线中获得，即。则在两个传感器在任意k的相对旋转满足下列方程（(9)的顺序有点疑惑）：

        

        通过将多个不同时刻的观测组成一个超定方程

        

        其中表示权重，其由一个启发式方法来确定以降低外点的影响（代码里面计算使用的是轴角表示时的旋转角度，threshold为1.0）：

        

        

        其中为四元数的实部，方程(10)可以由的最小的奇异值对应的右单位特征向量得到。

        对于手眼标定的顺序问题，我找到一段代码，是通过两个lidar时间作为IMU时间，通过IMU的拟合轨迹得到两个时刻的IMU位姿，然后通过激光雷达和IMU之间的相对变换矩阵得到两时刻对应lidar的相对位姿

// 两个时刻LiDAR的相对位姿获取，LiDAR的相对旋转是由IMU的相对旋转和标定矩阵获得
bool TrajectoryManager::evaluateLidarRelativeRotation(double lidar_time1,
        double lidar_time2, Eigen::Quaterniond &q_L2toL1) const {
  assert(lidar_time1 <= lidar_time2
         && "[evaluateRelativeRotation] : lidar_time1 > lidar_time2");

  double traj_time1 = lidar_time1 + lidar_->time_offset();
  double traj_time2 = lidar_time2 + lidar_->time_offset();

  if (traj_->MinTime() > traj_time1 || traj_->MaxTime() <= traj_time2)
    return false;

  Result result1 = traj_->Evaluate(traj_time1, EvalOrientation);
  Result result2 = traj_->Evaluate(traj_time2, EvalOrientation);
  Eigen::Quaterniond q_I2toI1 = result1->orientation.conjugate()*result2->orientation; // 左乘：result1*q_I2toI1 = result2

  q_L2toL1 = calib_param_manager->q_LtoI.conjugate() * q_I2toI1 * calib_param_manager->q_LtoI; // 手眼标定公式
  return true;
}

        对于平移的初始化，非常的困难。首先，加速度四谷体验重力向量和旋转耦合的。因此在旋转的B样条曲线的对齐误差会影响平移的B样条曲线精度。并且B样条曲线的二次微分会在方程(1)的u向量中引入两个0元素，这也让控制点不可解。因此，使用IMU的测量值来初始化平移不可靠，所以我们忽略了平移外参的初始化，从实验测试来看会对标定结果有较小的影响。

        初始化代码的解读：主要是方程(9)(10)

bool InertialInitializer::EstimateRotation(
        TrajectoryManager::Ptr traj_manager,
        const Eigen::aligned_vector& odom_data) {

  int flags = kontiki::trajectories::EvalOrientation;
  std::shared_ptr p_traj
          = traj_manager->getTrajectory(); // kontiki优化结果中获取轨迹

  Eigen::aligned_vector A_vec;
  // 每次取出相邻两个数据
  for (size_t j = 1; j < odom_data.size(); ++j) {
    size_t i = j - 1;
    double ti = odom_data.at(i).timestamp;
    double tj = odom_data.at(j).timestamp;
    if (tj >= p_traj->MaxTime()) // 后一个里程计数据超出时间范围，则跳出
      break;
    auto result_i = p_traj->Evaluate(ti, flags); // 获取对应时刻IMU的ti时刻的姿态
    auto result_j = p_traj->Evaluate(tj, flags);
    Eigen::Quaterniond delta_qij_imu = result_i->orientation.conjugate()
                                       * result_j->orientation;

    Eigen::Matrix3d R_Si_toS0 = odom_data.at(i).pose.topLeftCorner<3,3>();
    Eigen::Matrix3d R_Sj_toS0 = odom_data.at(j).pose.topLeftCorner<3,3>();
    Eigen::Matrix3d delta_ij_sensor = R_Si_toS0.transpose() * R_Sj_toS0; // dT
    Eigen::Quaterniond delta_qij_sensor(delta_ij_sensor);

    // 求解超参
    Eigen::AngleAxisd R_vector1(delta_qij_sensor.toRotationMatrix()); // 转换为轴角形式
    Eigen::AngleAxisd R_vector2(delta_qij_imu.toRotationMatrix());
    double delta_angle = 180 / M_PI * std::fabs(R_vector1.angle() - R_vector2.angle()); // 旋转绝对角度的差值
    double huber = delta_angle > 1.0 ? 1.0/delta_angle : 1.0; // 两个旋转角度差的阈值1.0rad

    Eigen::Matrix4d lq_mat = mathutils::LeftQuatMatrix(delta_qij_sensor); // 构建左乘和右乘矩阵
    Eigen::Matrix4d rq_mat = mathutils::RightQuatMatrix(delta_qij_imu);
    A_vec.push_back(huber * (lq_mat - rq_mat));
  }
  size_t valid_size = A_vec.size();
  if (valid_size < 15) {
    return false;
  }
  Eigen::MatrixXd A(valid_size * 4, 4);
  for (size_t i = 0; i < valid_size; ++i)
    A.block<4, 4>(i * 4, 0) = A_vec.at(i);

  Eigen::JacobiSVD svd(A, Eigen:: | Eigen::ComputeFullV); // 奇异值从大到小排列
  Eigen::Matrix x = svd.matrixV().col(3);
  Eigen::Quaterniond q_ItoS_est(x); // vector4d初始化，实部在后方式一：4个标量

  // Quaterniond q1(1, 2, 3, 4);   // 第一种方式  实部为1 ，虚部234
  // Quaterniond q2(Vector4d(1, 2, 3, 4));  // 第二种方式Vector4d  实部为4 ，虚部123

  Eigen::Vector4d cov = svd.singularValues();

  if (cov(2) > 0.25) { //最小的奇异值>0.25
    q_ItoS_est_ = q_ItoS_est;
    rotaion_initialized_ = true;
    return true;
  } else {
    return false;
  }
}

        代码需要注意的是，四元数表示方法为虚部在前，实部在后，所以q的左右矩阵生成函数于实部在前的四元数表示方法不一样，两者刚好对角交换。

// 四元数虚部在前，实部在后，于Quaternion kinematics 的顺序不一样
template
inline Eigen::Matrix LeftQuatMatrix(const Eigen::Matrix &q) {
  Eigen::Matrix m;
  Eigen::Matrix vq{q.x(), q.y(), q.z()};
  T q4 = q.w();
  m.block(0, 0, 3, 3) << q4 * I3x3 + SkewSymmetric(vq);
  m.block(3, 0, 1, 3) << -vq.transpose();
  m.block(0, 3, 3, 1) << vq;
  m(3, 3) = q4;
  return m;
}

template
inline Eigen::Matrix RightQuatMatrix(const Eigen::Matrix &p) {
  Eigen::Matrix m;
  Eigen::Matrix vp{p.x(), p.y(), p.z()};
  T p4 = p.w();
  m.block(0, 0, 3, 3) << p4 * I3x3 - SkewSymmetric(vp);
  m.block(3, 0, 1, 3) << -vp.transpose();
  m.block(0, 3, 3, 1) << vp;
  m(3, 3) = p4;
  return m;
}

        Eigen的svd结果的奇异值从大到小排列。

        注意Eigen::Quaternion的初始化方式的不同，代码里面使用的是Vector4d初始化，其代表的四元数实部在后

Quaterniond q1(1, 2, 3, 4);   // 第一种方式  实部为1 ，虚部234
Quaterniond q2(Vector4d(1, 2, 3, 4));  // 第二种方式Vector4d  实部为4 ，虚部123

Eigen::Matrix x = svd.matrixV().col(3);
Eigen::Quaterniond q_ItoS_est(x); // vector4d初始化，实部在后方式一：4个标量

        对求解的四元数的判断使用奇异值。这里借用的使用0.25左阈值，是一个经验值，这里和VINS-Mono一样。一般对于线性方程的求解结果的稳定性与矩阵的条件数相关，条件数越大，则解受噪声影响越大，越不稳定。而条件数为最大奇异值和最小奇异值的比值。（参考 数值计算方法 清华大学）

if (cov(2) > 0.25) { //最小的奇异值>0.25
    q_ItoS_est_ = q_ItoS_est;
    rotaion_initialized_ = true;
    return true;
  } else {
    return false;

          Ax=0的最优估计求解：

B 面元地图和数据关联

        通过初始的和旋转曲线，IMU可以为LiDAR scan数据提供旋转的预测，可以用来去除旋转畸变，这对提高LiDAR里程计的精度和LiDAR点云地图的质量。因此，我们将将点云地图离散为3D cells，并计算每个cell里的点的一阶和二阶动量。代码里面使用的时ndt_omp算法，可以直接得到点云的cell，动量，特征值和特征向量。

plane_lambda_ = 0.7;
surfel_association_->setPlaneLambda(plane_lambda_);
auto ndt_omp = LiDAROdometry::ndtInit(ndt_resolution_);
ndt_omp->setInputTarget(scan_undistortion_->get_map_cloud()); // 将点云输入ndt_omp，借助ndt_omp来计算每个cell的性质
surfel_association_->setSurfelMap(ndt_omp, map_time_);



// 每个格子拟合平面，并且给不同cell的内点不同颜色
void SurfelAssociation::setSurfelMap(
        const pclomp::NormalDistributionsTransform::Ptr& ndtPtr,
        double timestamp) {
  clearSurfelMap();
  map_timestamp_ = timestamp;

  //mCellSize = ndtPtr->getTargetCells().getLeafSize()(0);

  // check each cell
  Eigen::Vector3i counter(0,0,0);
  for (const auto &v : ndtPtr->getTargetCells().getLeaves()) { //leaves报保存的是map leaf保存当前cell的信息
    auto leaf = v.second;

    if (leaf.nr_points < 10) // cell点数要>10
      continue;
    // leaf直接可以获取
    int plane_type = checkPlaneType(leaf.getEvals(), leaf.getEvecs(), p_lambda_); //cell里的特征值和特征向量，用于判断是否为平面
    if (plane_type < 0)
      continue;

    Eigen::Vector4d surfCoeff;
    VPointCloud::Ptr cloud_inliers = VPointCloud::Ptr(new VPointCloud);
    if (!fitPlane(leaf.pointList_.makeShared(), surfCoeff, cloud_inliers)) // cell里的点RANSAC拟合平面，平面参数保存到surfCoeff中，平面内点保存到cloud_inliers中，inlier点数必须大与20
      continue;

    counter(plane_type) += 1; // -1 0 1 2
    // 平面信息保存
    SurfelPlane surfplane;
    surfplane.cloud = leaf.pointList_;
    surfplane.cloud_inlier = *cloud_inliers;
    surfplane.p4 = surfCoeff;
    surfplane.Pi = -surfCoeff(3) * surfCoeff.head<3>();

    // 平面包围框
    VPoint min, max;
    pcl::getMinMax3D(surfplane.cloud, min, max);
    surfplane.boxMin = Eigen::Vector3d(min.x, min.y, min.z);
    surfplane.boxMax = Eigen::Vector3d(max.x, max.y, max.z);

    surfel_planes_.push_back(surfplane);
  }

  spoint_per_surfel_.resize(surfel_planes_.size());

  std::cout << "Plane type  :" << counter.transpose()
            << "; Plane number: " << surfel_planes_.size() << std::endl;

  // 给平面上色
  surfels_map_.clear();
  {
    int idx = 0;
    for (const auto &v : surfel_planes_) {
      colorPointCloudT cloud_rgb;
      pcl::copyPointCloud(v.cloud_inlier, cloud_rgb);

      size_t colorType = (idx++) % color_list_.size(); // 点云颜色
      for (auto & p : cloud_rgb) {
        p.rgba = color_list_[colorType]; // 每个点给不同颜色
      }
      surfels_map_ += cloud_rgb;
    }
  }
}

面元可以使用下列平面相似度参数来识别[32]:

        

        其中，他们是二阶动量矩阵的特征值。对于平面分布的cell来说，。因此，如果平面相似度参超过一个阈值（第一次优化前为0.6，后面为0.7），我们就认为这个cell里的点是平面。

        对应代码：

int SurfelAssociation::checkPlaneType(const Eigen::Vector3d& eigen_value,
                                      const Eigen::Matrix3d& eigen_vector,
                                      const double& p_lambda) {
  Eigen::Vector3d sorted_vec;
  Eigen::Vector3i ind;
  Eigen::sort_vec(eigen_value, sorted_vec, ind); //sorted_vec由大到小排排列

  double p = 2*(sorted_vec[1] - sorted_vec[2]) /
             (sorted_vec[2] + sorted_vec[1] + sorted_vec[0]);

  if (p < p_lambda) { // 小于阈值，不是平面
    return -1;
  }

  int min_idx = ind[2]; // 最小特征值对应列的特征向量为平面的法向量
  Eigen::Vector3d plane_normal = eigen_vector.block<3,1>(0, min_idx); // 对应列
  plane_normal = plane_normal.array().abs();

  Eigen::sort_vec(plane_normal, sorted_vec, ind);
  return ind[2];
}

        当判断为平面之后则使用RANSAC算法拟合平面，得到。

// cloud RANSAC拟合平面，平面参数保存到coeffs中，平面内点保存到cloud_inliers中，inlier点数大与20
bool SurfelAssociation::fitPlane(const VPointCloud::Ptr& cloud,
                                 Eigen::Vector4d &coeffs,
                                 VPointCloud::Ptr cloud_inliers) {
  pcl::ModelCoefficients::Ptr coefficients (new pcl::ModelCoefficients);
  pcl::PointIndices::Ptr inliers (new pcl::PointIndices);
  pcl::SACSegmentation seg;    /// Create the segmentation object
  // Optional
  seg.setOptimizeCoefficients (true);
  // Mandatory
  seg.setModelType (pcl::SACMODEL_PLANE);
  seg.setMethodType (pcl::SAC_RANSAC);
  seg.setDistanceThreshold (0.05);

  seg.setInputCloud (cloud);
  seg.segment (*inliers, *coefficients);

  if (inliers->indices.size () < 20) {
    return false;
  }

  for(int i = 0; i < 4; i++) {
    coeffs(i) = coefficients->values[i];
  }

  pcl::copyPointCloud (*cloud, *inliers, *cloud_inliers);
  return true;
}

需要注意的是所有平面和LiDAR地图都是相对于坐标系的。我们从小的cell中提取平面可以让我们能充分利用环境中的所有平面区域，以给批量优化提供更可靠的约束。为了更鲁棒，当点到平面距离大一个阈值的时候，我们就会舍弃这个约束。为了降低运算量，我们对于原始的LiDAR进行降采样。

C 连续时间批量优化

        系统估计的状态量为

        其中的和分别代表III中描述的连续时间轨迹的旋转和平移控制点。是一个二维旋转矩阵，可以将IMU参考系的z轴对齐到重力向量方向。角速度计和陀螺仪的零偏假设是由高斯白噪声影响。一般来说，标定问题都可以公式化为图优化问题。给定一系列关系的LiDAR点L，线加速度观测A，角速度观测W，和以上所有观测都受独立高斯噪声的影响的假设。

// add constraints
addGyroscopeMeasurements(estimator_split);
addAccelerometerMeasurement(estimator_split);
addSurfMeasurement(estimator_split, surfels_association);

        最大概率估计问题p(x|L,A,W)可以通过解最小二乘方程求解：

        

        其中分别代表加速度计，陀螺仪，LiDAR观测的残差。分别代表相应的方差矩阵。特别的是，IMU残差定义为：

        

        

        其中为IMU在时刻的原始测量数据。对于关联点，其在时刻捕捉到，且于平面关联，则点到平面的距离里为：

             

        我们使用LM算法优化方程（15），并迭代估计状态。   

        这里对点到面的距离进行解读，代码在lidar_surfel_point.h中，如下：

        这部分挺烧脑的，首先我们需要牢记几点：

        1. 整篇文章中利用B样条曲线拟合的都是IMU的轨迹，不是激光雷达的轨迹，他们两者就是由我们的标定外参所关联。

        2. 激光雷达点云地图的初始时刻和IMU的初始时刻不一致，但起始都是单位矩阵，所以如果我们得到地图时刻map_time_(地图构建的起始时刻，此是地图轨迹对应位姿为单位矩阵)和激光点时刻(timestamp_)的IMU轨迹上对应坐标，还需要得到map_time_时IMU轨迹位姿相对于timestamp_的坐标，这样再转换回去才能得到激光点在地图坐标系下的坐标。

        下面进行步骤的详细解读：

        已知：点云地图中的一个平面，以及关联上这个平面的一个原始激光雷达帧的激光点（激光雷达坐标系），IMU轨迹；

        目的：获取此激光点在点云地图上的坐标，以此计算点到平面的距离。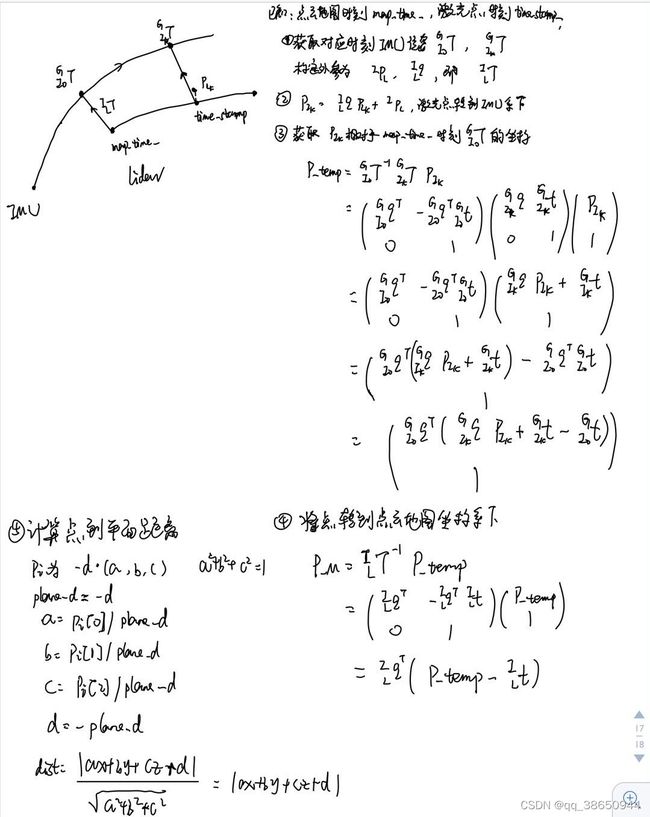         

  // 误差函数 将当前点投影到地图中，计算点面误差，这个投影的姿态矩阵使用的是拟合的轨迹得到的位姿
  template
  Eigen::Matrix reprojectPoint2map(const type::Trajectory& trajectory,
                                            const type::LiDAR& lidar,
                                            const T* plane_cp) const {
    int flags = trajectories::EvaluationFlags::EvalPosition | trajectories::EvaluationFlags::EvalOrientation;

    auto T_I0toG = trajectory.Evaluate(T(map_time_) + lidar.time_offset(), flags); // 当前激光地图时刻对应的IMU轨迹上的IMU数据的全局位姿，此时对于激光雷达轨迹而言，此时是单位矩阵，所以需要进行抵消
    auto T_IktoG = trajectory.Evaluate(T(timestamp_)+ lidar.time_offset(), flags); // 当前激光点时刻对应的IMU轨迹上的IMU数据的全局位姿

    const Eigen::Matrix p_LinI = lidar.relative_position();
    const Eigen::Quaternion   q_LtoI = lidar.relative_orientation();

    Eigen::Matrix p_Lk = lidar_point_.cast(); // 当前激光雷达的位姿，这里使用的是原始的激光雷达数据
    Eigen::Matrix p_Ik = q_LtoI * p_Lk + p_LinI; // 得到激光雷达点在当前IMU坐标系下的坐标

    Eigen::Matrix p_temp = T_I0toG->orientation.conjugate()*(T_IktoG->orientation * p_Ik + T_IktoG->position - T_I0toG->position); // 激光雷达点在Ik时刻IMU坐guiji1ssd标系下的坐标相对于I0时刻的相对位姿
    Eigen::Matrix p_M = q_LtoI.conjugate() * (p_temp - p_LinI); // 激光雷达在激光雷达世界坐标系（激光雷达地图）下的坐标

#if 1
    Eigen::Matrix Pi = Eigen::Map>(plane_cp);
    T plane_d = T(Pi.norm()); // plane_d = -d  // Pi = -surfCoeff(3) * surfCoeff.head<3>() = -d*(a,b,c)
    T plane_norm[3];
    plane_norm[0] = T(Pi[0])/plane_d; // a
    plane_norm[1] = T(Pi[1])/plane_d; // b
    plane_norm[2] = T(Pi[2])/plane_d; // c

    T dist = ceres::DotProduct(plane_norm, p_M.data()) - plane_d; // 使用点面距离
#else
    T plane_d = T(plane_[3]);
    T plane_norm[3];
    plane_norm[0] = T(plane_[0]);
    plane_norm[1] = T(plane_[1]);
    plane_norm[2] = T(plane_[2]);
    T dist = ceres::DotProduct(plane_norm, p_M.data()) + plane_d;
#endif

    Eigen::Matrix error(dist);
  //  error.topLeftCorner(1,1) = T(dist);
  //  Vector3 error_vector = dist * p_L / p_L.norm();

    return error;
  }

                                     

 D 调整

        连续批量优化以后，估计的状态（包含外参）会更加精确。因此我们使用当前的最优估计来对原始LiDAR scan去除畸变，重新构建LiDAR面地图，更新点到面的数据关联。注意的是，基于LiDAR里程计的NDT配准只在开始初始化LiDAR位姿和LiDAR地图时使用。在第一次和第二次批量优化时的典型的LiDAR面元地图如Fig3所示。地图质量在一次优化后大大提升。仅仅几次迭代（实验中为4次），所提算法已经收敛，可以给出一个高精度的标定结果。

V 实验

        我们设计了仿真和实际传感器的实验。实际中的LiDAR和IMU使用硬件同步[33]，我们只关心两个传感器的空间标定结果。在代码中，我们使用Kontiki[34]做连续时间批量优化。

        代码里面仍然对时间偏移量进行了估计，就是在加入点到面的距离残差时，给点找对应时刻的位姿时，给时刻加了一个偏移量。这里的理解是B-Spline使轨迹可微，进而可以计算梯度，进而可以优化。这里需要说明一下我的时延标定实验结果：我是用提供的时间同步后的数据，手动加了50ms的偏移，但是最终迭代3次，标定出来的时间偏移只有6ms，不知道是不是我的操作有问题，还是原本这种方法标定的时延就不太准确，希望感兴趣的同学可以一起交流一下。

auto T_I0toG = trajectory.Evaluate(T(map_time_) + lidar.time_offset(), flags); // 当前激光地图时刻对应的IMU轨迹上的IMU数据的全局位姿，此时对于激光雷达轨迹而言，此时是单位矩阵，所以需要进行抵消
auto T_IktoG = trajectory.Evaluate(T(timestamp_)+ lidar.time_offset(), flags); // 当前激光点时刻对应的IMU轨迹上的IMU数据的全局位姿

        实际采数据时，所有的数据序列的平均绝对角速度为47.39度/s，加速度为0.628。为了获得精确的结果，我们必须保证在所有数据中有充足的线加速度和角速度激励，样条曲线的结点空间分布设置为0.02sec来解决高动态运动。轨迹评估使用ATE

VI github上的一些问题整理

        1. 可以使用这个代码来标定2D lidar和IMU吗？

            可以，当前只有初始化和数据关联步骤使用了NDT里程计，它不能用于2D雷达。但是refinement与lidar的线的数量无关，所以推荐修改一下激光雷达里程计。

        2. 可观测性分析

            based on the observability of IMU-LiDAR extrinsic calibration[1,2], at least two rotations about different axes are necessary. Meanwhile, large accelerations and angular velocities make the estimation more accurate, but you should make sure the error of the LiDAR odometry is within a certain range under that severe motion.

        [1] LIC-Fusion 2.0 https://arxiv.org/pdf/2008.07196.pdf (Section IV. OBSERVABILITY ANALYSIS)
        [2] Hesch, Joel. (2016). Consistency Analysis and Improvement for Vision-aided Inertial Navigation. Retrieved from the University