【配准论文解读】Color Point Cloud Registration with 4D ICP Algorithm
本文是对于IEEE ICRA2011的论文《Color Point Cloud Registration with 4D ICP Algorithm》做一解读,这篇文章主要介绍了一种通过HSV加权实现点云配准的方法,如有不正之处,欢迎斧正!
一、Abstract
本文介绍了使用相关图像中的色调数据加速3D点云配准的方法。通过在传统三维坐标下加入加权的图像色调信息,构成新的四维空间,并使用k-d树最近邻搜索寻找对应点,加快了收敛速度。使用色彩辅助HSV色彩空间来进行4D的ICP配准。同时,使用奇异值分解(SVD)方法迭代的求解配准所需的平移和旋转矩阵。
二、Introduction
生成高精度的3D地图是包括测量、救援、安全、防御及建筑等许多领域的热点问题。基于激光的扫描设备已经应用于生成点云,其描绘了关于物体和环境的空间信息[1]。这些扫描仪使用精确的高速旋转仪器和传感器生成高密度3D点云。来自彩色相机的相应光学图像也可以与3D点云相关联以产生视觉上逼真的3D色点云。3D彩色点云包含距离和纹理信息,它们提供了更丰富的扫描环境表示,并更容易识别扫描的对象[2]。
通过从多个位置获取3D扫描信息,可以生成大规模的3D地图。 在不同位置获取的各个扫描必须基于有利位置和方向信息组合在一起作为完整的大比例尺地图。从两个彼此足够接近的有利位置获得的关联点云的算法可以分为迭代最近点(ICP)相关技术,ICP变体相关技术和非ICP技术。在迭代最近点(ICP)算法中使用点对点关联策略。 它是点云映射配准最流行的配准算法[3]。 在ICP算法中,不同点云中的最近点被关联起来,并且迭代地计算最小化两个数据集的相关点之间的分离的均方误差的最佳刚性变换[8]。收敛后,ICP算法已被证明以最小误差终止[9]。通过奇异值分解(SVD)方法[10],矩阵系统方法和双四元数技术通常用于确定两点云中匹配点之间的最小平均距离[11]。近年来,基于SVD的算法由于其鲁棒性和易于实现而被广泛用于ICP和6D SLAM [12,13,15]。
通过将彩色相机集成到定制的3D LIDAR [14]上,可以生成3D色点云。通过在混合传感器系统上应用适当的校准[13,16],可以将距离测量和视觉信息集成在一起,以构建场景的视觉逼真和几何精确的表示。彩色映射的3D数据用于通过使用加权的红色,绿色,蓝色数据来注册单个3d扫描。在ICP过程中,可以基于尺寸和颜色数据完成相应的点搜索。每个点的色调(来自Hue-saturation-lightness模型)被分类并用作过滤器以约束每次ICP迭代中的最近点搜索[17,18]。通过尺度不变特征变换(SIFT),可以使用距离图像上的颜色数据来估计成对扫描的初始对齐,对YIQ颜色模型中传输的颜色属性进行加权,以构建新的变量以及ICP精确配准的范围信息[16]。深度插值图像特征(DIFT)算法基于提取的对应关系解决了2个图像和寄存器颜色点云之间的对应点[19]。概率扫描配准跟踪激光束以利用最大范围读数来增加对准的可能性[20]。点云表面正态分布有助于粗略配准。点云表面法向量分布可以作为扩展高斯图像(EGI)[21]转换为方向直方图,并且可以从交叉协方差函数[22]求解不同扫描之间的刚性运动。通过在SO(3)(SOFT)上计算旋转群上的离散傅里叶变换,可以在傅里叶域中求解刚体运动[23]。色彩属性已经应用于正态分布变换(NDT)过程中的核扩展,从而提高了鲁棒性[23]。在大多数情况下,基于常规的配准方法应用于点云粗略对齐,基于ICP的算法用于精确配准。
本文介绍了一种色调辅助4D ICP算法,该算法利用彩色激光测距系统的数据。 关键思想是将加权色调值与3D坐标数据一起应用,以提高点对准速度和准确度。 点关联发生在解决3D点云图对齐可能发生的模糊处理。 ICP过程中点关联的性能可以通过色调数据来提前。
三、彩色点云数据的生成
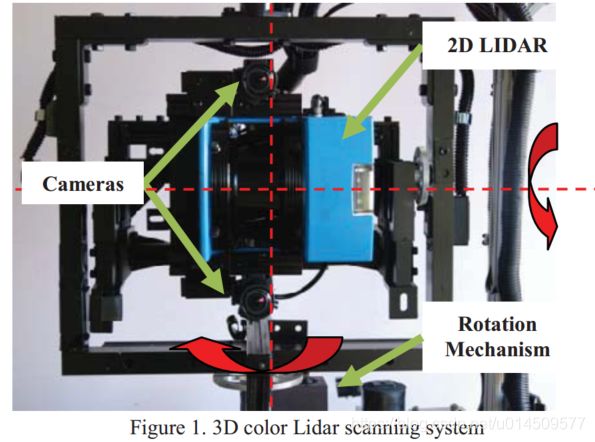
通过使用视频配准的3D LIDAR扫描系统来创建色点云。 该系统利用安装在旋转机构顶部的2D LIDAR扫描仪。 LIDAR定向为产生垂直2D扫描,并且机构围绕垂直轴旋转。 旋转位置传感器用于在每次扫描期间测量机构的角度,并且用作用于产生3D扫描的球面坐标系的第三维度。 校准的高速摄像机安装在扫描仪上,用于实时着色3d数据(图1)。
扫描仪安装在名为ROAMS(远程操作和自主映射系统)的移动电动平台的顶部,以便能够生成大规模地图(图2)[13]。 该系统可以从远距离无线操作,并且可以生成远程位置的地图。 为了生成大比例尺的地图,ROAMS被驱动到扫描区域周围的各个位置,并且在每个位置处进行3d彩色扫描。
四、色调辅助ICP算法
可以应用色调值来增加点关联的准确性。 ICP过程中的大部分时间和计算成本都花在试图找到正确的点对上。 最近的空间距离规则用于典型的3D ICP方法。 通过将加权色调值添加为第四维,可以将3D空间中的点云距离值扩展为4D空间。 通过将色调值整合到最近点搜索中,可以提高点关联的准确性。
A.优势点的色调不变性
对于从两个有利位置拍摄的图像之间的相同点,色调值保持一致,而以红色,绿色和蓝色量表示的颜色值通常因光照条件的变化而不同。为了有效地应用颜色来改善关联过程,应该去除照明效果。原始RGB颜色数据被转换为单独的色度,亮度和亮度值的表示。图3显示了两个相机图像在Rubik立方体上的调色板的不同角度拍摄,在同一表面上使用四种颜色。图3还显示了去除背景和黑框的彩色像素。直方图图4显示了所有像素在RGB空间中的红色,绿色和蓝色值。在RGB直方图中,图像的R,G和B分布随着有利位置变化很大。当RGB颜色空间被转换为HSL空间并且色调,亮度和饱和度的直方图被绘制在图5中时,色调值对于相机的位置保持相对不变。因此,从色调饱和度 - 亮度(HSL)模型中获取的像素的色调值被用作色点关联处理中的第四维度。
B.色调辅助ICP的算法
色调和范围值必须在4D ICP变量中组合为{xo,yo,zo,ho}以进行点关联。其中,![]() 是原始的距离空间的位置坐标,
是原始的距离空间的位置坐标,![]() 是原始的颜色值。颜色值被归一化为[0,1]区间中,并且必须在四维空间中的最近点搜索期间加权。
是原始的颜色值。颜色值被归一化为[0,1]区间中,并且必须在四维空间中的最近点搜索期间加权。![]() 是标准化和加权的色调值。 为了标准化坐标,使用扫描仪的最大范围,并将坐标空间重新调整为0-1范围。点关联的归一化变量是
是标准化和加权的色调值。 为了标准化坐标,使用扫描仪的最大范围,并将坐标空间重新调整为0-1范围。点关联的归一化变量是![]() ,其中,
,其中,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 是lidar的最大范围。
是lidar的最大范围。
应正确选择色调维度的权重值以进行点关联。 由于范围和色调值都从0到1归一化。色调的权重表示其在最近邻搜索过程中的影响。 低权重使点关联偏向于范围数据,并且偏向色调值的高权重。 色调的小重量值对应于传统的3D-ICP。 实验结果表明,色调权重10%和3D范围搜索距离的35%产生了精确点关联的最佳结果。 通过计算相关点对的平均均方根距离来评估4D ICP中的误差。
颜色辅助ICP算法的主要步骤:
1、估算矩阵R和T的初始值,该矩阵将数据点云中的点转换为模型点云的坐标系。
2、构造模型点云M {m1,m2,m3 ... mM}的k-d树,加权色调值为第4维;
3、While merging error > preset tolerance:
- 使用R和T将数据点云进行旋转:
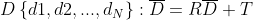
- 最近点关联步骤:
- for i = 1:num_point:
- set number of associated point N=0
- 在模型k-d树中搜索点di {dix,diy,diz,dih}的最近点
- 如果最近的点mj存在于指定的搜索范围内,则r将di和mj关联为{dk,mk};
- 增加关联点数++:
- for i = 1:num_point:
- 距离误差计算:对于每个关联的点对,将标准化均方根距离
 计算为误差:
计算为误差:
- 求解最小化
 的R和T:构造正交矩阵H(方程7)并求解刚性旋转R和平移T(方程8和9)
的R和T:构造正交矩阵H(方程7)并求解刚性旋转R和平移T(方程8和9) - 注册后错误估计:计算任何后期注册错误,例如平面度或曲率连续性。
C、基于点云协助信息的K-d树
在3D ICP算法中,根据最近距离规则搜索对应点。 这可能在单次迭代循环期间导致不正确的匹配,并且对于给定的数据点集合需要多于1次迭代来配对正确的最近邻居点。 基于正确的色调属性,可以在一次迭代中找到模型中的最佳邻居。根据正确的颜色信息,相应的点可以用较少的迭代锁定。
ICP计算速度和精度高度依赖于关联过程。 使用k-d树进行最近点搜索和关联或最近邻搜索(NNS)问题可提高搜索的速度和效率。 k-d树是空间分区数据结构,其在k维空间中存储和组织数据。 k-d树是广义类型的二叉树,每个叶节点是k维数据点,其将超空间分成两个子空间。 从第一维到第k维依次进行分裂。
可以在k-d树上非常有效地进行最近邻搜索。 对于在数据点云和搜索半径中具有已知坐标的给定点,算法递归地向下移动树并遵循与插入相同的过程。 搜索在树的叶节点处停止,并且识别搜索半径内的模型树中的点。 使用距离计算获得最近的点,然后将其视为与搜索点相关联的点。
在3D最近点搜索中,2个相邻点云中的2个点之间的距离为: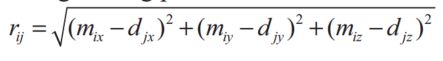 。其中,di {dix,diy,diz}和mj {mjx,mjy,mjz}分别是数据和模型点云图中的点空间坐标。在4D空间中,每个点的第四维应该加权色调值dhw和MHW。 点的空间值应通过方程式中的3D搜索半径rij进行归一化。(1)。 为了在4D空间中完成最近点搜索,两个归一化点di {dix,diy,diz ,, hihw}和mj {mjx,mjy,mjz,mjhw}之间的距离应为:
。其中,di {dix,diy,diz}和mj {mjx,mjy,mjz}分别是数据和模型点云图中的点空间坐标。在4D空间中,每个点的第四维应该加权色调值dhw和MHW。 点的空间值应通过方程式中的3D搜索半径rij进行归一化。(1)。 为了在4D空间中完成最近点搜索,两个归一化点di {dix,diy,diz ,, hihw}和mj {mjx,mjy,mjz,mjhw}之间的距离应为:
在ICP过程中,搜索半径会影响计算时间和最终结果。 对所有迭代应用恒定搜索半径。 如果搜索半径很大,则在关联期间将包括太多点作为候选者。 另一方面,如果搜索半径很小,则点可能不相关,并且将需要更多的迭代。 最佳搜索半径取决于点云的密度和初始位置估计。 在4D k-d树搜索中,搜索半径基于坐标数据以及加权色调,如公式1所示。(3)。 根据经验,通常选择搜索半径以产生大约50个候选点。如果在4-D空间的构造中使用相当大的权重,则kD搜索将偏向于色调维度,并且4D ICP算法将表现接近于 a将hue-filter应用于系统。
严格基于坐标的关联可能导致非唯一配准。 例如,如果模型中的点和数据点云属于平面,则基于坐标的ICP将导致点的非唯一关联。 在这种情况下,使用色调值可能导致点的唯一配准。
D、误差最小化
如果![]() 表示模型点云中第i个点的坐标,ddddj = {,,}} jx jy jz是相关或成对点集中第j个点的坐标,距离误差定义为:
表示模型点云中第i个点的坐标,ddddj = {,,}} jx jy jz是相关或成对点集中第j个点的坐标,距离误差定义为: 。
。
对于模型和数据点云中的关联点计算质心,如公式5所示。 坐标被转换为具有在等式6中给出的质心的原点。 可以构建关联点的标准正交变换矩阵(公式7)。 旋转R和平移T是分离的。 使用奇异值分解(SVD),R可以从正交性矩阵(方程式8)求解。 通过平移模型和数据点集的质心来计算平移T: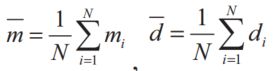
![]() 是模型和数据点云中关联点的质心.N是关联点的总数。 转换后的坐标是:
是模型和数据点云中关联点的质心.N是关联点的总数。 转换后的坐标是: 。
。 是第i个关于变换坐标系的关联点。可以构造正交性矩阵H:
是第i个关于变换坐标系的关联点。可以构造正交性矩阵H:
对H矩阵执行奇异值分解以确定旋转矩阵R,其将误差最小化为: ![]() 。最终旋转矩阵为
。最终旋转矩阵为![]() ,平移T被定义为:
,平移T被定义为: 。
。
五、实验部分
A、已知的6DOF转换点云段注册
该实验比较了3D ICP和4D ICP之间的配准速度,用于两个点云,其登记变换是先验已知的。两种算法都应用于从移动测绘机器人[13]获得的地图上。在6DOF,相同的点云已经转换为新的视点。从原始空间围绕Y轴和Z轴选择新的视图位置10°。分别选择转换为距离2.46,2.612和0.347的X,Y,Z轴。错误比较和相关的点数比较如图6(a)和图6(b)所示。关联稳定性如图6(c)所示,以说明该过程的收敛性。经过102次迭代后,4D ICP完成配准,传统的3D ICP在164次迭代后收敛。这说明4D ICP算法的收敛速度比3D ICP更快,点搜索提供更准确的p关于建筑物的合并色点云。
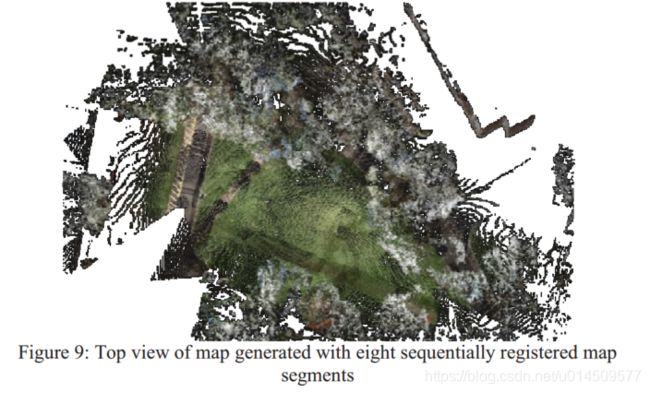
B、在未知变换的大型场景点云配准
选取了室外场景的8个不同地点的点云图像,k-d树的搜索半径设置为0.0094,彩色值被归一化为0到1,颜色过滤范围设置为0.15,颜色的权重被设置为0.0023(接近3D搜索范围的25%)。
可以看出4D ICP比传统的3D ICP需要更少的迭代次数。 该多个地图段顺序登记实验说明了将色调维度添加到大规模地图构造的配准进度的效果。 例如,位置3和4获取的点云在配准前已经显示在图10中,注册点云显示在图11中,图11(a)描述了具有两种不同颜色的两种不同点云,位置4处的点云(黑色) )已经注册到位置3点云(蓝色)。 具有颜色的组合点云如图11(b)所示。